从等差向等比类比

● (太湖中学，安徽 太湖 246400)

2017-07-08

李昭平(1963-)，男，安徽太湖人，安徽省特级教师.研究方向数学教育.

从等差向等比类比

●李昭平
(太湖中学，安徽 太湖 246400)

类比,通常是指由某类事物的特征类比出另一类事物的相应特征的一种思维方式和解题思想.等差数列和等比数列之间联系紧密、规律和谐、辩证统一，这些为等差向等比类比提供了保证.从等差数列的性质、形式、条件、等式、解法可以类比出等比数列相应的性质、形式、条件、等式、解法等.

等差数列；类比；等比数列；逻辑证明

从等差向等比类比，往往融直观想象、逻辑推理、数学运算等数学核心素养于一体，能有效培养学生的直觉思维能力、合情推理能力和探究证明能力[1].从等差数列的性质可以类比出等比数列的性质；从等差数列问题的结构形式可以类比出等比数列问题的结构形式；从等差数列的充要条件可以类比出等比数列的充要条件；从等差数列满足的等式可以类比出等比数列所满足的等式；从等差数列问题的解法可以类比出等比数列问题的解法.下面分享几个类比结论，从中体会类比的魅力.

1 性质类比

例1我们知道，若等差数列{an}的前n项和为Sn，则对任意m∈N*,Sm,S2m-Sm,S3m-S2m也成等差数列.类比到等比数列，则有：若等比数列{an}的前n项和为Sn，则对任意m∈N*,Sm,S2m-Sm,S3m-S2m(其中Sm≠0)也成等比数列.

说明以上两道题是大家熟悉的，均由等差数列的性质类比出等比数列的相应性质.例1中要注意在等比数列中，必须满足Sm≠0；例2的结论中“和差”变成了“积商”，这是由等比数列的本质决定的.

2 形式类比

例3在等差数列{an}中，若a2+1,a4+3,a6+5成等比数列，则其公比是1.理由是：因为a2,a4,a6成等差数列，1,3,5也成等差数列，所以a2+1,a4+3,a6+5成等差数列.于是a2+1,a4+3,a6+5既是等差数列又是等比数列，则为非零的常数列，故其公比是1.由此向等比数列类比，写出一道试题，并解之.

分析类比题:在等比数列{an}中，若2a1,6a3,18a5成等差数列，则其公差是______．

事实上，因为a1,a3,a5成等比数列，2,6,18也成等比数列，所以2a1,6a3,18a5成等比数列.于是2a1,6a3,18a5既是等比数列又是等差数列，则为非零的常数列，故其公差是0.

说明从形式类比，例2中等差、等比数列的性质可以一般化，即“在等差数列{an}中，若am+bk,ap+bs,aq+bt成等比数列，且am,ap,aq和bk,bs,bt均成等差数列，则其公比是1”和“在等比数列{an}中，若ambk,apbs,aqbt成等差数列，且am,ap,aq和bk,bs,bt均成等比数列，则其公差是0”[2].

例4在数1和100之间插入n个实数，使得这n+2个数构成递增的等差数列，将这n+2个数的和记作Tn，再令an=10Tn，n≥1.

1)求数列{an}的通项公式；

2)由此向等比数列类比，写出一道试题，并解之.

分析1)设t1,t2,…,tn+2构成等差数列，其中t1=1,tn+2=100，则

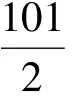
因此

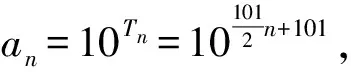
2)类比题：在数1和100之间插入n个实数，使得这n+2个数构成递增的等比数列，将这n+2个数的乘积记作Tn，再令an=lgTn,n≥1.求数列{an}的通项公式.

事实上，设t1,t2,…,tn+2构成等比数列，其中t1=1,tn+2=100，则

式(1)×式(2)并利用titn+3-i=t1tn+2=102(其中1≤i≤n+2),得

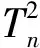
从而

an=lgTn=n+2,其中n∈N*.

说明从试题结构形式上类比，即“递增的等差数列变成递增的等比数列”“n+2个数的和记作Tn变成n+2个数的乘积记作Tn”“再令an=10Tn变成再令an=lgTn”.

3 条件类比

例5设数列{an}的前n项和为Sn,不难得到：数列{an}为等差数列的充分必要条件是：对任何n∈N+,都有Sn=An2+Bn(其中A,B是常数).由此向等比数列类比，写出结论，并证明之.

分析类比结论：设数列a1,a2,…,an,…中的每一项都不为0，且前n项和为Sn,则数列{an}为公比非1的等比数列的充分必要条件是：对任何n∈N+,都有Sn=kqn-k(其中k,q是非零的常数).

只证充分性(必要性易证，略去)：当n≥2时，

an=Sn-Sn-1=(kqn-k)-(kqn-1-k)=

k(q-1)qn-1；

当n=1时,

a1=S1=kq-k=k(q-1),

从而

an=k(q-1)qn-1,其中n∈N+.

因此{an}是等比数列.

说明从等差数列的和式充要条件类比到等比数列的和式充要条件.

例6设数列a1,a2,…,an,…中的每一项都不为0.我们能得到：{an}为等差数列的充分必要条件是：对任何n∈N+,都有

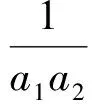
此结论反映了等差数列概念的又一种表达方式.由此向等比数列类比，写出结论，并证明之.

分析类比结论：设数列a1,a2,…,an,…中的每一项都为正数，则{an}为等比数列的充分必要条件是：对任何n∈N+,都有

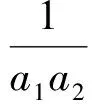
只证充分性(必要性易证，略去)：由

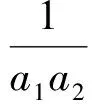
和

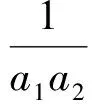
整体相除，得

即

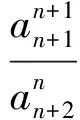
同理可得

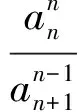
于是

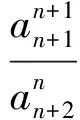
而数列a1,a2,…,an,…中的每一项都为正数,从而

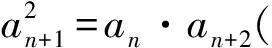
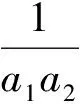
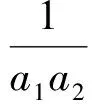
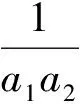
4 等式类比

例7在等差数列{an}中，若a2 018=0,则等式a1+a2+a3+…+an=a1+a2+a3+…+a4 035-n(其中n<4 035,n∈N*)成立.类比此等式，相应地，在等比数列{bn}中，若b2 017=1,则有______成立.

分析因为a4 036-n+i+an-i=2a2 018=0(其中0≤i≤n-1),且

2(a4 036-n+a4 037-n+a4 038-n+…+an)=(a4 036-n+an)+(a4 037-n+an-1)+(a4 038-n+an-2)+…+(an+a4 036-n)=0,所以a4 036-n+a4 037-n+a4 038-n+…+an=0,

于是a1+a2+a3+…+an=a1+a2+a3+…+a4 035-n(其中n<4 035,n∈N*).

(b4 034-n·b4 035-n·b4 036-n·…·bn)2=(b4 034-n·b4 035-n·b4 036-n·…·bn)(bn·bn-1·bn-2·…·b4 034-n)=(b4 034-n·bn)(b4 036-n·bn-1)(b4 035-n·bn-2)·…·(bn·b4 034-n)=1,所以b4 034-n·b4 035-n·b4 036-n·…·bn=1,于是b1·b2·b3·…·bn=b1·b2·b3·…·b4 033-n(其中n<4 033,n∈N*).

说明从等差数列{an}满足的等式类比到等比数列{bn}满足的等式，充分运用an+am=ap+ap和bn·bm=bp·bq(其中n+m=p+q).

5 解法类比

例8在等差数列{an}中，对某些正整数s，t(其中s≠t),当as=at时，{an}必是常数列.类比此结论，在等比数列{bn}中，对某些正整数s，t(其中s≠t),当as=at时，{bn}也是常数列吗？

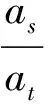
当s-r为奇数时，q=1，{bn}是常数列；当s-r为偶数时，q=±1，{bn}是项的绝对值相等、相邻项异号的非常数列.

说明从等差数列{an}的解法类比到等比数列{bn}的解法，获得结论.

以上8个例题很好地展现了等差数列与等比数列在定义、通项、求和公式、基本性质等方面的联系和区别.利用两者异同规律进行类比,往往会得到两种数列类似的结论.显然在证明过程中，也充分运用了解决数列问题的一些重要思想方法(函数思想、整体相减、整体相加、整体相乘、整体相除等).需要注意的是，类比的结论不一定都正确，需要逻辑证明.这给我们的启示是：类比是极好的研究性学习素材，关键在于教师要善于思考、善于发掘、善于研究、善于利用[3].

[1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003.

[2] 曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，1999.

[3] 李昭平.通过数学研究性学习培养学生科学素养[J].中学数学,2011(4)：12-14.

O122

A

1003-6407(2017)10-27-03