基于培育逻辑推理素养的章引言教学——以“推理与证明”的教学设计为例

● (鄞州高级中学，浙江 宁波 315100)

●任伟芳 (宁波市教育局教研室，浙江 宁波 315000)

2017-08-21

王世恩(1981-)，男，浙江宁波人，中学高级教师.研究方向数学教育.

基于培育逻辑推理素养的章引言教学
——以“推理与证明”的教学设计为例

●王世恩
(鄞州高级中学，浙江 宁波 315100)

●任伟芳
(宁波市教育局教研室，浙江 宁波 315000)

在章引言教学中培育逻辑推理素养需要引发学生学习兴趣，引导学生会学数学，引领学生在新章节中探索遨游．推理与证明是培育数学逻辑推理素养的抓手，是贯穿于高中数学整个知识体系的思维方式，是理性思维的重要部分．

逻辑推理；章引言；推理课堂；实践思考

近日，浙江省宁波市教研室组织了以“深化课程意识，培育核心素养”为主题的章引言课堂教学评比，章引言和核心素养教学引起了参会教师浓厚的兴趣．活动依托“推理与证明”等章引言内容开设了10节同课异构的评比课．笔者用新课程理念，根据授课内容特点和学生认知水平，通过注重培育逻辑推理素养所构建的“推理”课堂，得到评委教师和学生的一致好评．下面以这节人教A版《数学(选修2-2)》第2章“推理与证明”章引言教学设计为例，谈谈如何在章引言教学中培育逻辑推理素养的实践与思考．

1 教学内容的分析

推理与证明是一种数学的基本思维过程,也是人们学习和生活中经常使用的思维方式之一[1]．“推理与证明”作为一个独立的章节编入教材中是本次课程改革的一大亮点，说明它对学生能力发展的重要性．推理与证明是培育数学逻辑推理素养的抓手之一，是学生学好数学的基础，也是贯穿于高中数学整个知识体系的思维方式，是理性思维的重要部分．数学之所以区别于其他学科，在于数学规律的确定性必须由推理和证明来实现，因此“推理是数学的命根子”[2]．教材将推理与证明的一般方法进行了总结和归纳,把过去渗透在具体数学内容中的思维方法,以集中、显性的形式在一个章节中呈现出来，使学生更加明确这些方法,同时对后继知识的学习起到引领作用,并能在以后的学习中有意识地运用这些方法,从而达到系统化螺旋式地培育学生逻辑推理素养的目的．

2 课堂实录(片段)

2.1 环节1：创设问题情境，感受推理魅力

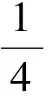
分析当生物体死亡后，它机体内原有的“碳14”会按确定的规律衰减，大约每经过5 730年衰减为原来的一半，这个时间称为“半衰期”．根据此规律，人们可以获得生物体内“碳14”含量P与死亡年数t之间的关系，由此可以推测化石距今约几万年．

师：下面请同学们举几个在日常生活中有关推理的例子？

生1：中华医学博大精深，中医师可以通过把脉来诊断出病人的病情．

生2：气温瞬息万变，气象专家可以通过云图分析和实践经验预测未来几天天气的状况．

设计意图请学生举例，说明推理在科学研究和日常生活等领域有着广泛的应用．数学推理是依据已有数学概念、生活经验、知识水平，运用归纳、类比、观察、猜想等推理方法，对数学事物或现象进行科学、合理地判断，继而得出一定的结论．因此学习推理可以帮助学生锻炼思维，科学客观地看待问题，会使人更聪明．

2.2 环节2：从特殊到一般的推理

师：有玩过如图1所示的这个游戏吗？今天我们来玩这个游戏．

图1

问题2在印度有个传说：在世界中心的神庙里，插着3根宝石柱子．印度教的主神梵天在创造世界的时候，在第一根柱子上从上到下穿了由小到大的64个纯金的圆盘．不论白天黑夜，总有一个僧侣按照如下规则移动圆盘，规则：

1)每次只能移动1个圆盘;

2)较大的圆盘不能放在较小的圆盘上面,僧人们预言：当所有圆盘都移到另一根柱子上时，世界将不复存在了．

师：这个预言会是真的吗？

生3：假的．

师：预言的真假本质上要研究怎样的问题？

生4：要解决64个圆盘从第一根柱子移到第二根柱子最少需要多少次的问题．

师：很好，首先我们把实际问题转化为数学问题．但64块圆盘的数量过大，我们应该怎么考虑？

生5：从1块圆盘开始，然后2块、3块、4块，依次下去……

师：接下来按课前分好的小组进行汉诺塔游戏的数学实验活动．活动要求：每个小组2人操作，1人记录移动步数(见表1)，1人最后汇报本组实验活动的情况，猜想f(n)=______．

表1 汉诺塔游戏的数学实验活动统计

(动手操作3分钟后．)

师：哪一组来分享本组的结果？

生6：我们组的实验结果:f(n)分别是1,3,7,15．

师：很棒！说一说是怎么移动的？

生7：这里关键是要用最快的速度将第一根柱子最底下一块移到第二根柱子上．比如：当有3块的时候，要将上面2块看成一个整体移动到第3根柱子上．因为将2块移到另一个柱子上最快要3次，所以总次数就是3+1+3=7次．

师：厉害！事实上，移动的过程就是一个推理过程．生活中人们往往需要进行这样那样的推理，比如在警察侦破案件、考古学家推测遗址年代等，这是我们为什么学习本章的原因．当有n个圆盘时，至少要移动几次呢？

生8：2n-1次.

设计意图引进汉诺塔的动手游戏，对于64个圆盘，有学生提出：64个圆盘数字太大不好处理，应该从1块圆盘开始，然后2块、3块、4块……依次下去，寻找规律更方便些，这是归纳推理最基本的思维方式．通过游戏活动，学生经历观察分析、逐渐发现结论的过程．在师生互动中渗透归纳推理，一方面能培养学生发现问题和提出问题的习惯;另一方面能优化学生的思维，启迪他们的智慧．

2.3 环节3：从一般到特殊的推理

师：像这种由特殊的几个概括得到一般结论的推理称为归纳推理，归纳推理与类比推理统称为合情推理，合情推理具有猜测和发现新结论的作用．刚才我们得到的结论是否一定正确呢？

生9：不一定正确．

问题3著名的费马猜想：任何形如22n+1(其中n∈N*)的数都是质数．

师：这个猜想在提出半个世纪后，被善于计算的欧拉发现，第5个费马数不是质数．同学们刚才的预判是正确的！由此可见，由归纳推理得到的结论需要证明．常见证明方法有直接证明和间接证明，还有将在本章学习的数学归纳法，数学归纳法适用于处理与正整数相关的数学命题．再回归到刚才得到的猜想，如果假定这个猜想是正确的，当有64块的时候，至少需要移动几次呢？

生10：264-1 ．

师：像这种从一般到特殊的推理过程称为演绎推理．假定僧侣们每秒移动一次圆盘，不停地移动需要多少年呢？我们一起来见证伟大而不可思议的数据18 446 744 073 709 511 615(秒)，换算成年，相当于大约5 846亿年．而地球的寿命最多还有100～150亿年，我们看到僧侣们的预言竟然是正确的！从汉诺塔的游戏开始，经历了推理中的归纳推理和演绎推理，本章还将学习一个从特殊到特殊的类比推理，譬如我们可将平面中的勾股定理类比推广到空间当中．看教材第97页小结中的知识结构，这就是本章我们要学习的内容．

设计意图培育逻辑推理核心素养需要有活动作为载体．通过动手实验把所有圆盘都移到另一根柱子上，在小组探究和成果分享中，使学生了解在进行归纳推理时，要搜集到一定的事实材料，有了个别性的、特殊性的知识作为前提，然后才能进行归纳推理．著名数学家波利亚曾说：“合情推理是冒险的，有争议的和暂时的”，通过费马猜想的反例告诉学生要养成“大胆猜想，小心求证”的严谨的科学态度．

2.4 环节4：俯瞰全貌，加强“会学”指导

师(小结)：本章怎么学呢？提两点学习建议：第一，我们既要用合乎情理的推理大胆猜想和发现未知的结论，又要合理运用数学证明的基本方法，对猜想的合理性进行证明，从而养成言之有理、论证有据的习惯；第二，了解全章的知识结构，能把书读厚，又能把书读薄，读薄就是抓住本质，抓住重点．最后，老师根据章引言的内容，自编一首歌曲作为本节课的结束，让我们愉快地开始本章的学习吧！

生(跟唱)：汉诺塔，真有趣，引领我们浏览“推理与证明”全貌，动手实验几分钟，归纳演绎显本质，医生诊断病症，警察侦破案情，专家预测天气，考古推断文物，大家论证命题，内涵推理证明，都挡不住数学眼光看穿它呀，相互合作、披荆斩棘、同心协力，培育我们逻辑推理素养．

设计意图“授之于鱼，不如授之以渔，这与学会学习的理念一致，‘会学’比‘学会’更重要”[3]．为了引导学生学习本章知识，提出全章的知识结构和学习建议．同时对学生进行学法指导——“推理”要言之有理，“证明”要论证有据．根据章引言中的有关介绍，自编了一首歌曲，既能使学生了解本章学习内容，又能激发学生的学习兴趣．

3 教学反思

3.1 做好章引言的引导者，培育逻辑推理素养更科学

在平时的教学中，章引言往往容易被遗忘．没有足够的课时，内容相对简单，种种理由让我们对其视而不见、弃之不用．如何使学生对本章将要学习的内容、结构，甚至思想方法有一个大致的了解，发挥章引言的“导游图”作用，应从以下3个方面着手：

1)为何引．章引言位于每个章节的起始位置，言简意赅地介绍了本章节所涉及的内容和思想方法，是章节内容的高度概括，起着提纲挈领的作用.它可以使学生初步了解该章节的学习目标、学习内容和学习方法．章引言还结合学习内容图文并茂地展示相关的知识背景、数学史与数学文化、现实生活中的应用．丰富的材料可以开拓学生的数学视野，激发学生的学习兴趣，让学生对即将开始的学习内容充满期待．

本节课首先列举了大量的生活实例，然后指出它们的关系与作用，再介绍本章的知识体系．这些材料可以让学生感受推理与证明源于生活和数学学习.通过章引言教学,学生不仅看到了知识的“来龙”，而且知道了它的“去脉”，了解了知识的发生、发展过程，这将有助于学生克服畏难情绪，充满自信地开始新知识的学习．

2)引什么．首先引发兴趣启发思考：教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞．章引言是激发学生学习兴趣、激活学生思维、鼓舞学生不断追求新知、充分调动学生学习主动性的重要教学环节．其次引出主题指明方向：引出本章的主题，介绍即将学习的内容，会涉及一些尚未学习的概念，此时没有必要对这些新概念一一解释，只需带领学生粗略地展望新的学习内容，了解概貌即可．当然，除了教学内容之外，更应该尽力渗透学习方法、学习策略的指导，关注对学生思维、思想的引领，在开启新篇章之际，引领学生入门．

本节课通过汉诺塔游戏引发兴趣启发思考，使学生经历从特殊到一般、再从一般到特殊的过程，从而为后续学习奠定基础．同时课堂中丰富的生活实例和汉诺塔游戏的数学建模，引导学生用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达世界．

3)怎么引．设计切实可行、自然平顺的章引言教学需要结合具体内容，去提炼生活中的数学，去思考知识发生发展的逻辑，去洞悉学生思维的最近发展区．学习的关键在于学生的悟，但也离不开教师的引．

本节课第4个环节教师提出本章学习的两点建议和自编歌曲的跟唱，目的是挖掘章引言的内涵和价值，引发学生的学习兴趣，引导学生“会学”数学，引领学生在新的章节学习中探索遨游．

3.2 利用独立成章优势，培育逻辑推理素养更完美

“推理与证明”独立成章的设置，让学生感受合情推理、演绎推理和数学证明在数学命题的发现、猜想与数学体系建构中的重要作用，有利于学生掌握推理与证明的思维方法．

1)以游戏为主线激发兴趣为培育逻辑推理素养创造条件．汤姆逊语:“数学不应被想象为一种费解而又违背常识的东西.实际上,数学正是常识的精微化.”数学由于是常识的精微化,它具有系统性强、抽象程度高的特点，因而本节课引入章头图中汉诺塔游戏贯穿始终，将本章推理与证明中涉及到的重要概念如合情推理、演绎推理包含其中．先提出汉诺塔传说中“预言会是真的吗”这个问题,激发学生的学习兴趣;然后通过动手实践、小组合作，探究当有n个圆盘时至少需要移动的次数，学生在前面的铺垫下很容易归纳出猜想的结论;最后又回到“预言会是真的吗”的话题，寓教于乐的教学设计激发了学生学习的兴趣，为提升素养创造了条件．

2)用导图引领思维为培育逻辑推理素养提供保障．在逻辑推理核心素养的形成过程中，学生能够发现问题和提出命题,能掌握推理的基本形式，理解数学知识之间的联系，建构知识框架,形成有论据、有条理、合乎逻辑的思维品质，这些都离不开思维导图的引领．本节课由浅入深，由简单到复杂，不断深化，思维的导图如图2所示：

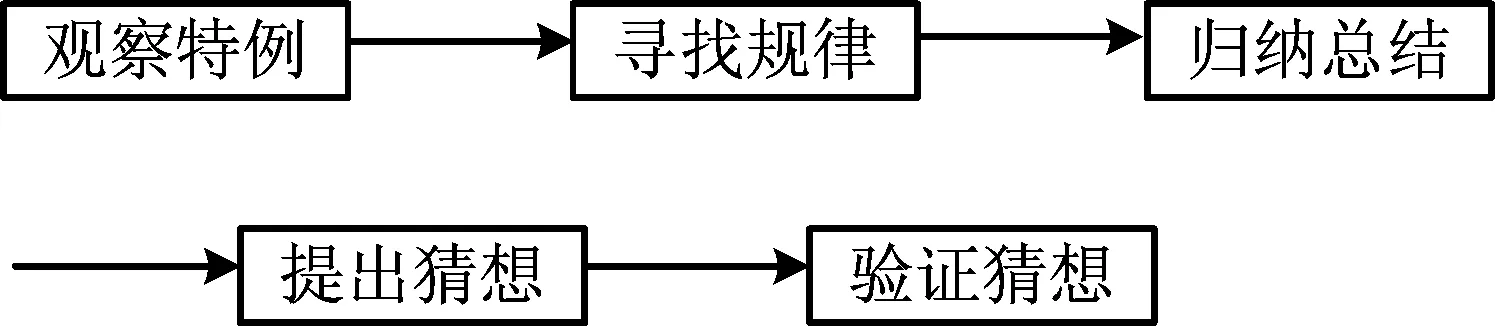
图2

在提出猜想后没有进行严格证明猜想，因而举了著名的费马猜想例子，说明在大胆猜想的同时还要小心求证，这样的教学设计不会影响推理的完整性和知识的严密性．

为了总体把握知识体系，为后续学习作好准备，在总结环节给出了本章的知识结构的思维导图(如图3所示)：

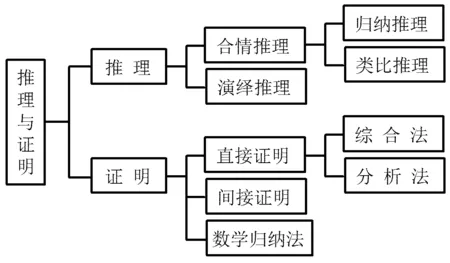
图3

3)处理好合情与演绎、推理与证明关系是培育逻辑推理素养的根本．长期以来在数学学习中一直强调其严谨性，过分渲染演绎推理的重要性而忽视了生动活泼的合情推理， 使人们误认为数学就是一门纯粹的演绎科学．事实上数学发展史中的每一个重要的发现，除演绎推理外，合情推理也起着重要作用．因此在数学学习中，既要强调思维的严密性和结果的正确性，也要重视思维的直觉探索性和发现性，即应重视数学合情推理的合理性和必要性，从而达到“合情与演绎相辅相成，推理与证明相得益彰”的最高境界．

“推理与证明”章引言教学中培育逻辑推理素养，需要在实践中勇于创新，不断探索．只有教师运用启发性的教学设计，构建高效的数学“推理”课堂，在趣味化的推理中优化学生的思维品质、发展自主学习能力，才能让学生满怀乐趣与憧憬去开始新一章的学习．

[1] 张奠宙.数学教育随想集[M].上海：华东师范大学出版社，2013：51-55.

[2] 史宁中. 数学的基本思想 [J]. 数学通报，2011(1)：1-9.

[3] 王尚志. 如何在数学教育中提升学生的数学核心素养[J]. 中国教师，2016(9)：33-38.

[4] 章建跃. 数学教育之取势明道优术 [J]. 数学通报，2014(10)：1-6.

O12

A

1003-6407(2017)10-09-04