基于基本图形的自然解法

● (鄞州实验中学，浙江 宁波 315100)

2017-06-19

蔡卫兵(1976-)，男，浙江象山人，中学高级教师.研究方向数学教育.

基于基本图形的自然解法

●蔡卫兵
(鄞州实验中学，浙江 宁波 315100)

文章从基本图形出发，尝试通过添加辅助线来解答初中几何问题，从而找到解题的切入口，顺利地把条件与结论有机串联起来，使得解法简洁、流畅.基本图形是辅助线添加的源头，它驱动着思维起航，催生着解题思路的自然、连贯.

数学解题；基本图形；自然解法

1 题目再现

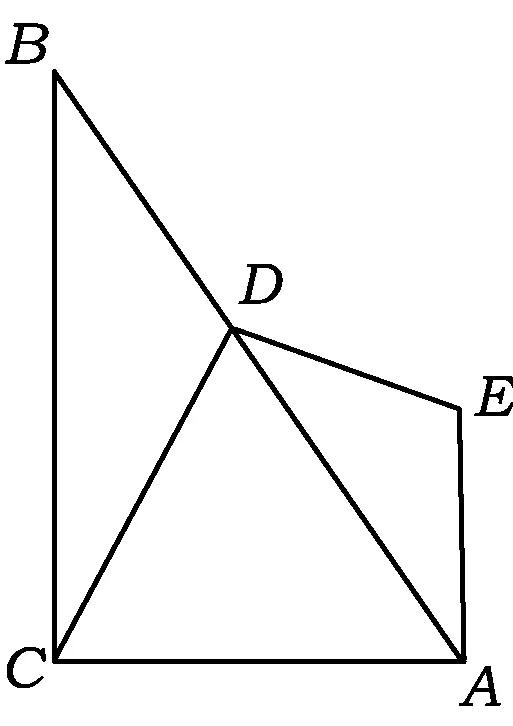
图1

题目如图1，在△ABC中，∠ACB=90°，∠CBA=30°，D是AB上任意一点，联结DC，作DE⊥DC，EA⊥AC，DE与AE交于点E，则DE,DC有什么数量关系？请给出证明.

本文基于6种基本图形(如图2所示)，用13种解法解决了该问题.

① ② ③

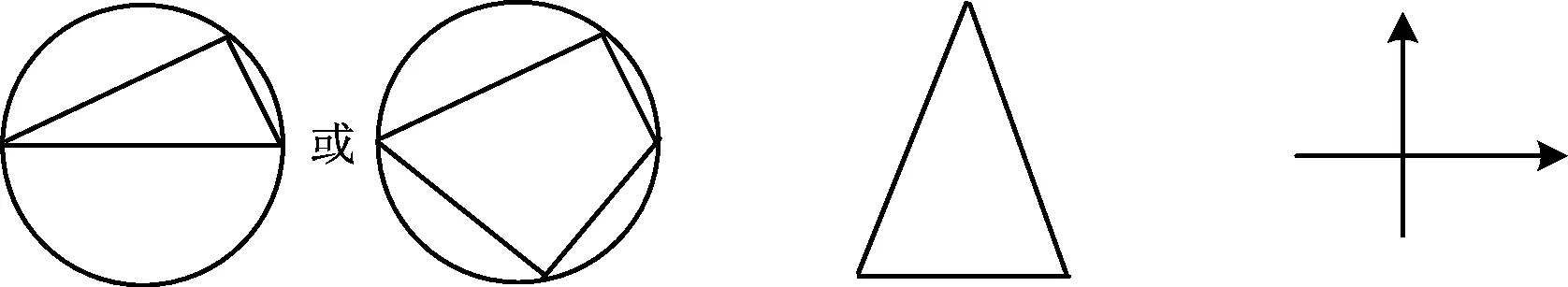
④⑤⑥

2 解法展示与思考

2.1 基本图形①

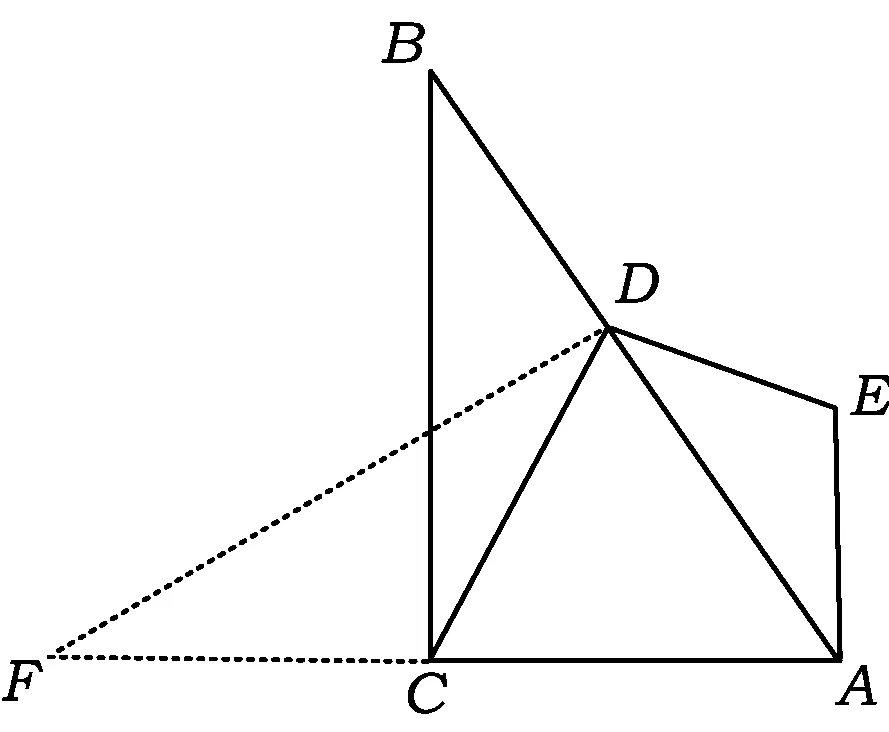
图3

解法1如图3，过点D作DF⊥AB,且DF与AC的延长线交于点F.因为DE⊥DC，所以

∠FDC=∠ADE.

又EA⊥AC，从而

∠F=∠DAE,

于是△FDC∽△ADE,进而

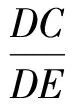
由∠ACB=90°，∠CBA=30°，知

∠FAD=60°.

因此在Rt△FDA中,

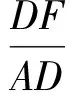
故

解法2如图4，过点D作DF⊥AB，且DF与AE的延长线交于点F.由解法1得

△ADC∽△FDE，

从而

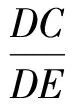
又由解法1得∠F=60°，于是

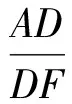
故

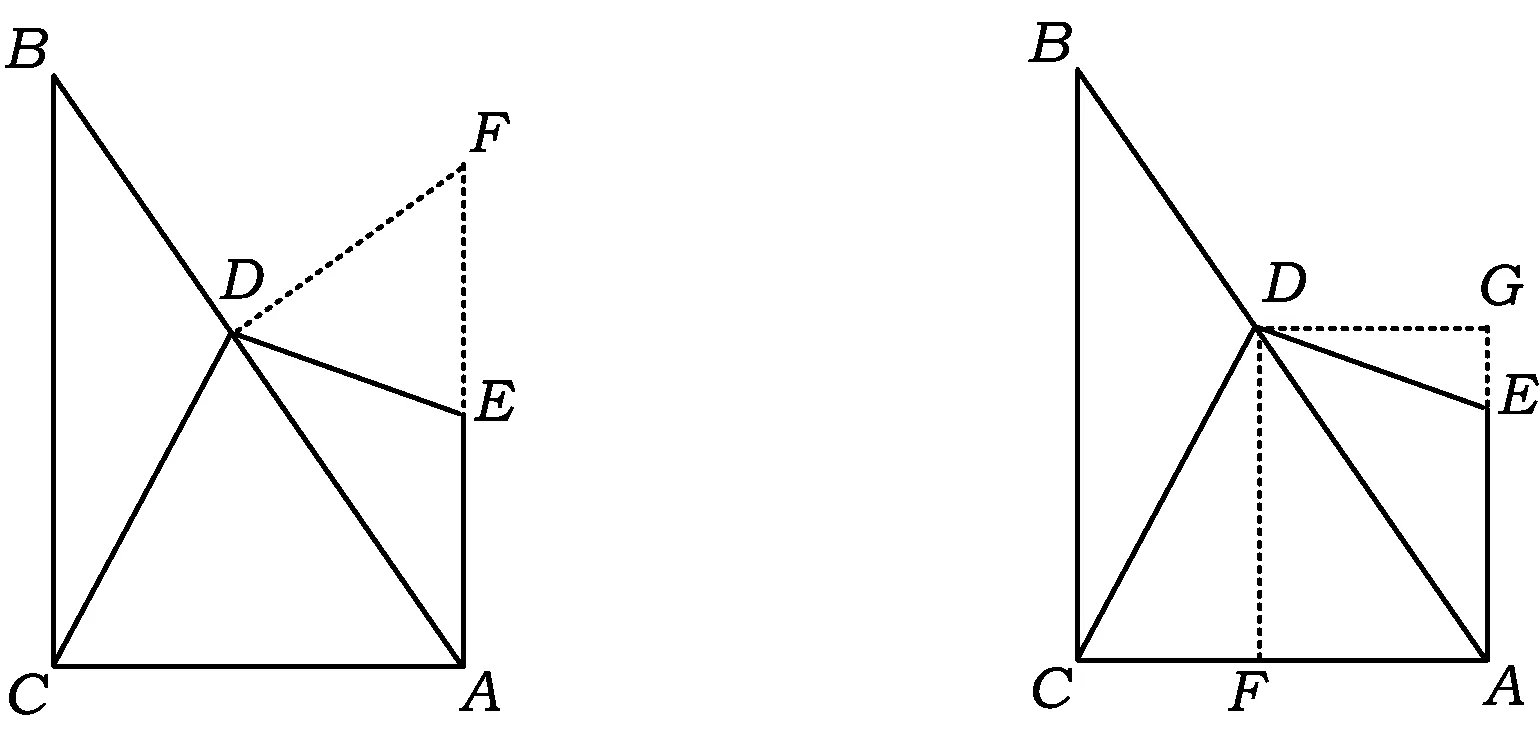
图4 图5

解法3如图5，过点D作DF⊥AC，DG⊥AE，垂足分别为F，G.由EA⊥AC可知四边形AGDF为矩形，从而DG=FA.同解法1得∠FAD=60°，于是

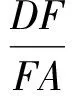
又∠CDF=∠EDG，从而

Rt△CDF∽Rt△EDG，

于是

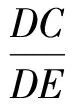
故

思考关于有公共顶点的双直角的基本图形模型，这是浙教版《数学》七年级上册“余角和补角”中的例题:指出图中哪些角是互余的？哪些角是相等的？显然根据同角的余角相等已证一对锐角相等，接着考虑将要求的两条线段DC,DE分别放到已得的一对角相等的两个三角形中，然后只需再证一对角相等便可判定两个三角形相似，借助相似三角形的对应边成比例将要求的“线段DC,DE之比”转化为“已知关系的两线段之比”.由于学生对此种基本图形模型比较熟悉，相似三角形的构造、判定、性质运用比较常见，因此解法1～3的辅助线容易想到，求解过程比较常规，是学生自然而然能想到的方法.

2.2 基本图形②

解法4如图6，过点D作GF⊥BC，且GF与BC交于点G，与AE的延长线交于点F.由∠ACB=90°，EA⊥AC可知四边形ACGF为矩形，从而CG=FA.易证∠DCG=∠FDE，于是

Rt△CDG∽Rt△EDF，

因此

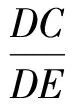
易得

∠FDA=60°，

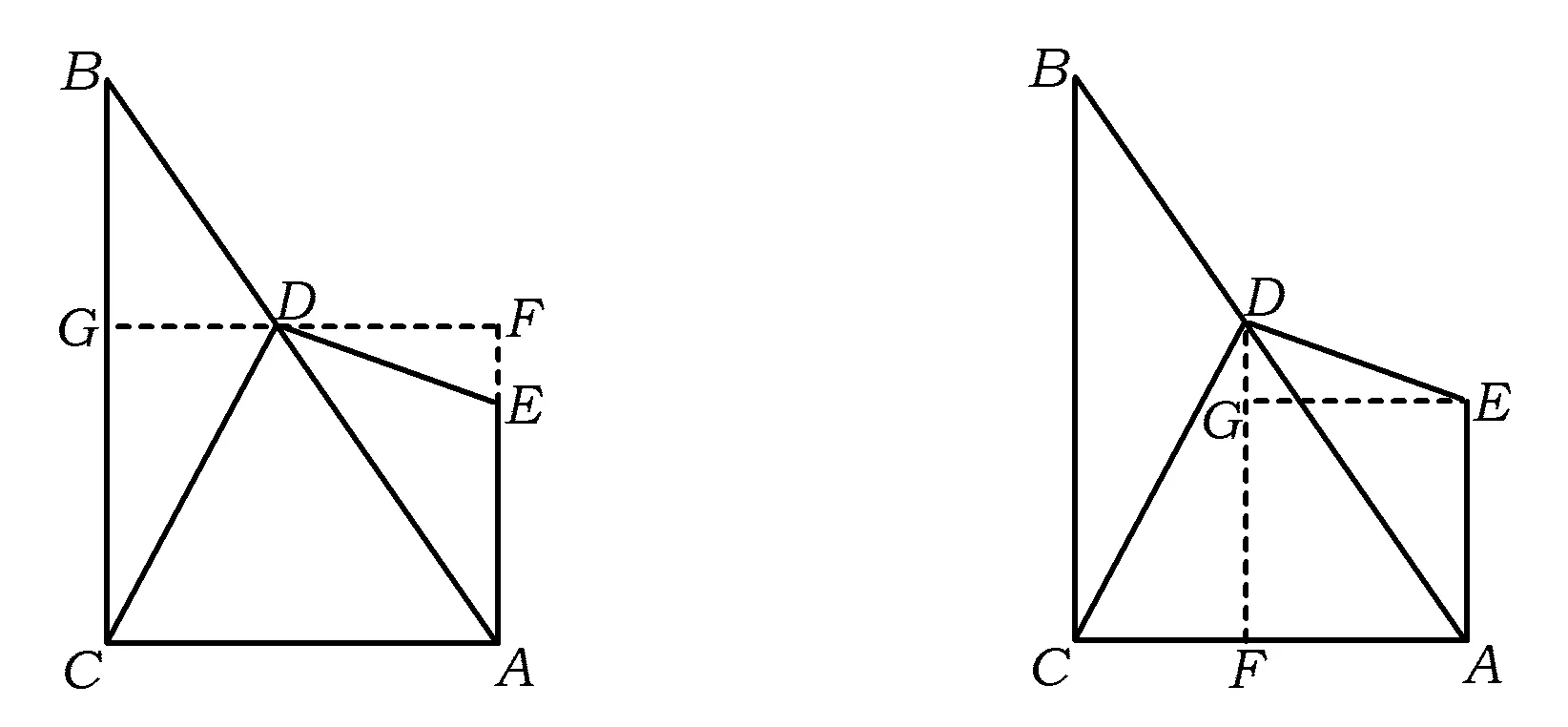
图6 图7

解法5如图7，过点D作DF⊥AC，垂足为F，过点E作EG⊥DF，垂足为G.同解法4可知四边形AFGE为矩形，从而EG=FA,同解法4又可得

Rt△CDF∽Rt△DEG，

于是

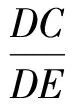
因为

所以

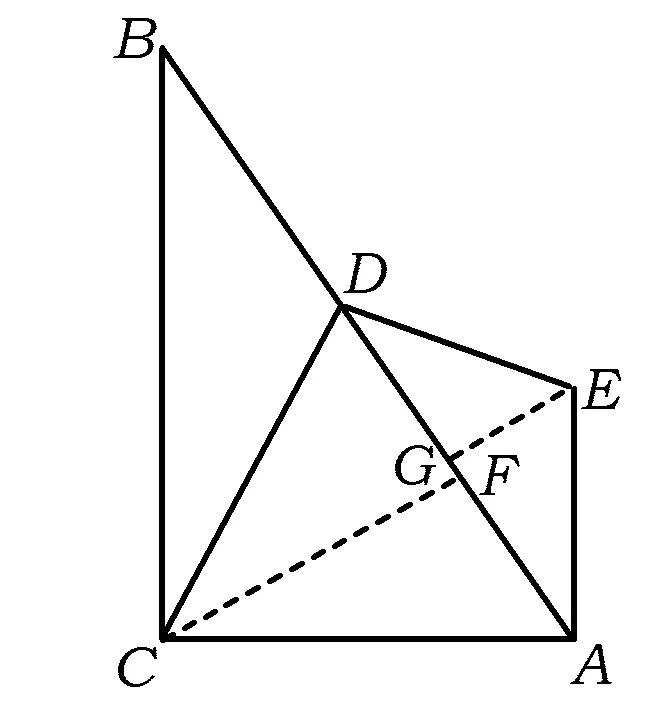
图8

解法6如图8，过点C作CF⊥AB，垂足为F，过点E作EG⊥AB，垂足为G.同解法5可得

Rt△CDF∽Rt△DEG，

从而

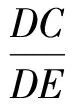
于是

CF·EG=DG·DF.

由Rt△ACF∽Rt△EAG,得

从而

CF·EG=AG·AF,

于是

DG·DF=AG·AF，

即

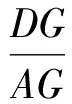
因此

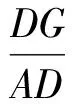
进而

DG=AF,

于是

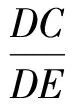
故

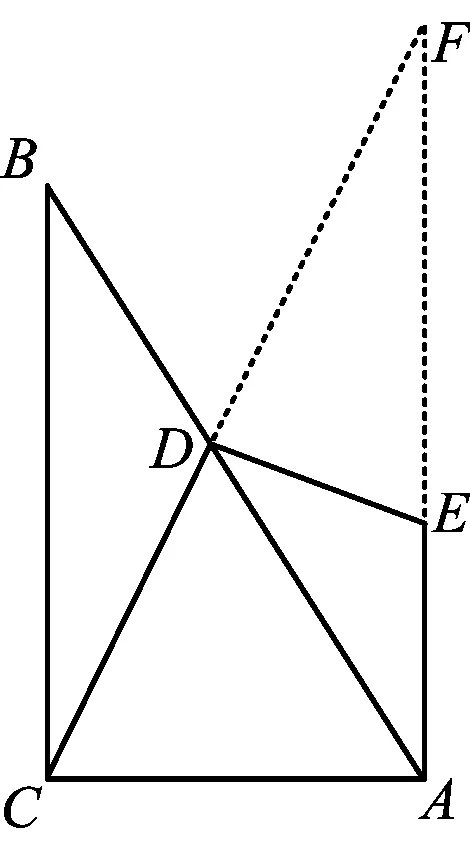
图9

思考关于3条边分别互相垂直的两个直角三角形的基本图形模型，这是浙教版《数学》八年级上册“全等三角形”和九年级上册“相似三角形”中的作业题，提炼模型：如果两个直角三角形对应边互相垂直，当对应边相等时，那么这两个直角三角形全等；当对应边不相等时，那么这两个直角三角形相似[1].解法4～6的本质相同，都是通过作辅助线构造“三垂直”相似模型，前两种线段之间的代换不涉及任何技巧，这也是比较接近学生的最近发展区的一种解题思路.其中解法6需要比例式与等积式之间的多次转化，运用合分比性质得出DG=AF使问题得解，其所蕴涵的思维量和所涉及的计算能力不是学生能自然而然所获得的.

2.3 基本图形③

解法7如图9，延长CD交AE的延长线于点F.由∠ACB=90°和EA⊥AC得BC∥AF，从而△BCD∽△AFD，于是

由∠F=∠F，∠FDE=∠FAC=90°得

△FAC∽△FDE，

从而

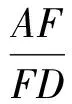
于是

因此

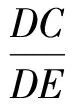
故

图10

2.4 基本图形④

解法8如图10，联结CE，作△CDE的外接圆，因为DE⊥DC，所以CE为圆的直径，又EA⊥AC，从而点A在以CE为直径的圆上，即点A,C,D,E在同一个圆上.由圆周角定理推论知

∠DEC=∠DAC=60°，

从而

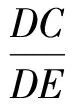
于是

思考“直径所对的圆周角是直角；90°的圆周角所对的弦是直径；圆的内接四边形的对角互补”是圆的基本性质，学生能比较熟练地想到运用上述性质，通过补上辅助的隐形圆，是此种解法的突破口，接着利用“同弧所对的圆周角相等”和锐角三角函数就能顺利求解.

2.5 基本图形⑤

解法9如图11，截取DF=DC，作∠GDA=∠EAD=30°.在四边形ACDE中,

∠CDE=∠CAE=90°，

从而

∠DCA+∠E=180°.

因为∠DFC+∠DFA=180°，∠DCF=∠DFC，所以

∠DFA=∠E.

又因为∠DAF=60°，∠DGE=∠GDA+∠EAD=60°，所以

∠DAF=∠DGE,

从而

△DAF∽△DGE，

于是

即

故

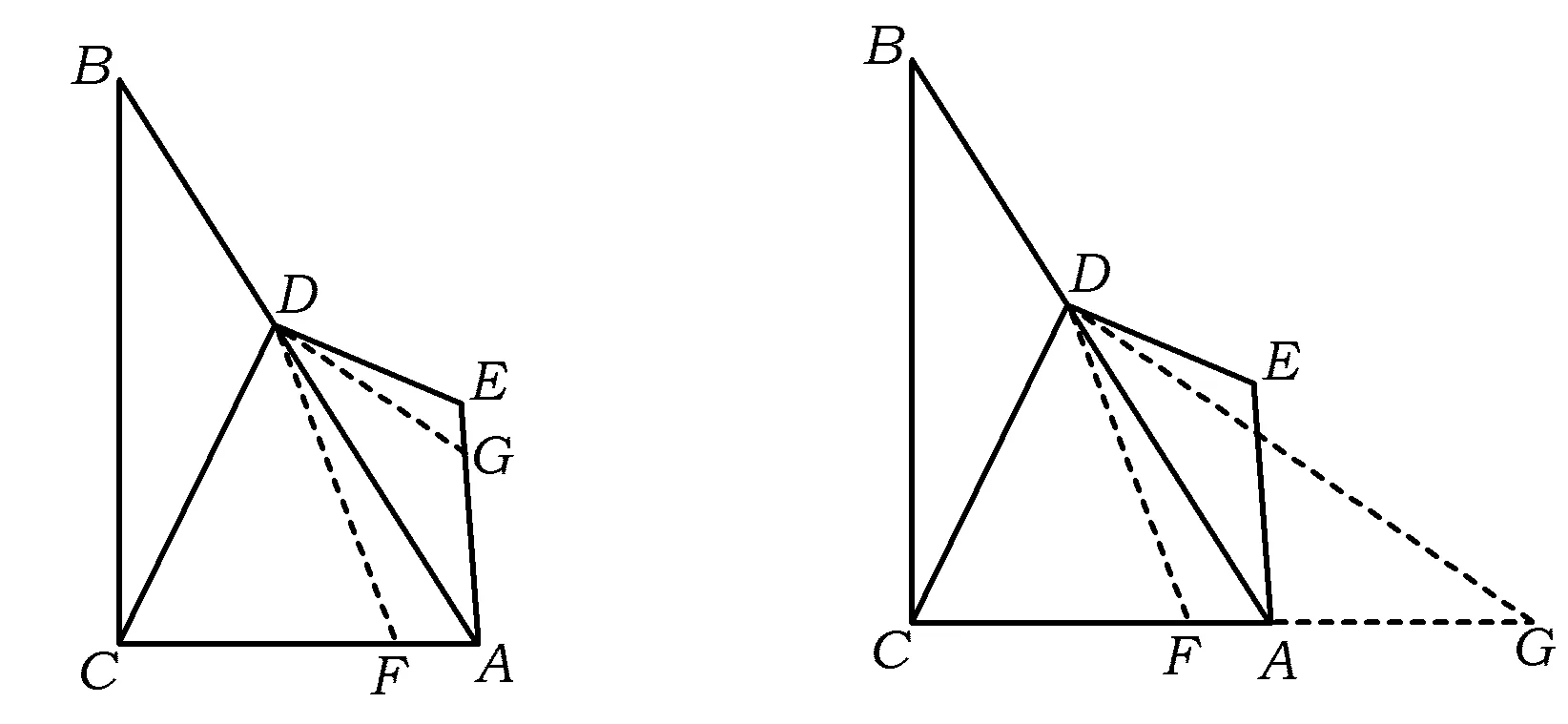
图11 图12

解法10如图12，截取DF=DC，AG=AD，联结DG.同解法9得

∠DFA=∠E,

因为∠DAF=∠G+∠ADG=60°，∠G=∠ADG，所以

∠G=30°.

又∠DAE=30°，从而

∠G=∠DAE,

于是

△DFG∽△DEA，

因此

于是

故

解法11如图13，截取DF=DE，作∠GDA=∠EAD.同解法9得

∠F=∠DCA， ∠DGF=∠DAC=60°,

从而

△DAC∽△DGF，

于是

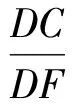
因此

故

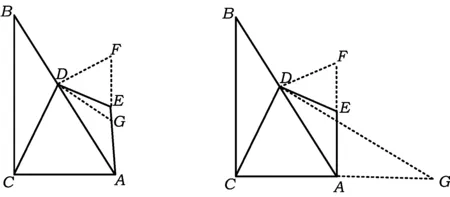
图13 图14

解法12如图14，截取DF=DE，AD=AG，联结DG.同解法10得

∠F=∠DCA， ∠DAF=∠G=30°,

从而

△DCG∽△DFA，

于是

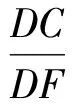
因此

故

思考以上4种解法本质相同，都是基于“等腰三角形的两腰相等进行线段之间的转化”和“等腰三角形的两底角相等进行角之间的转化”，接着依赖于视点的依次转换，顺势而思，通过构造包含相关的线段和已有的相等角的相似三角形：解法9和解法11再构造一对60°的角，解法10和解法12再构造一对30°的角，然后借助顶角为120°的等腰三角形的腰和底边之间的关系加以求解.这里解题思路的探寻一环扣一环，完全根据解题的需要，步步推进，但整个构造转化的过程较为复杂，学生获得这4种解法有一定的难度.

2.6 基本图形⑥

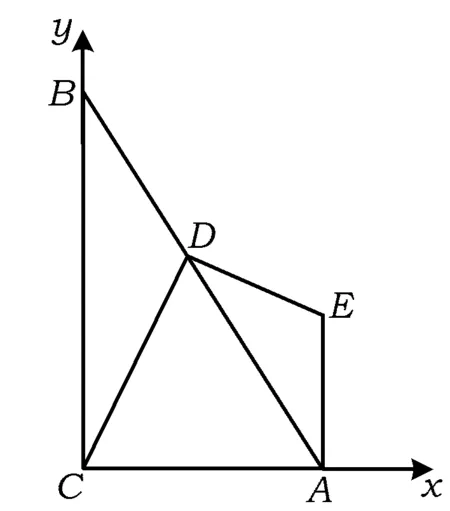
图15

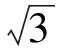
直线DE的解析式为

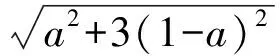
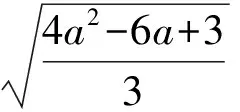
故

思考“定位”是坐标系特有的本领，根据本题的条件易将这个图形放在一个合适的平面直角坐标系中来思考，逐一定点、定线、定距离，通过“以数解形”使问题的解决水到渠成.用字母表示图中有关点的坐标或直线解析式或线段的长度，体现出符号意识，计算较繁琐，这是学生很难实现的“自然解法”.

3 反思

崇尚自然、重视常规而淡化技巧性是数学解题教学的一个方向和追求.方法的生成应该从学生已有的知识经验和思考基础出发，从记忆储存中提取有关的基本图形和常用结论,选择准确、科学的思维起点，使得解题的思路更加开阔，辅助线的添加也更为自然，从而催发方法自然生长[2].从思维的角度看，基于基本图形的数学模型解题体现思维定势正迁移的积极作用，化生为熟，化非常规为标准题的化归过程；从方法论的角度看，借助基本图形的数学模型思考问题，既可防止无关信息的负面干扰，又能以“块到块”的思维模式代替“点到点”的思维模式，提高思维的敏捷性.

在平时的解题教学过程中，教师要善于引导学生将所学的内容整理归纳出类型和方法，经过加工提炼，得出有长久保存价值的基本图形的数学模型，有意识地记忆下来，在新问题中唤醒头脑中积累的基本图形，并选择较简单的求解过程的数学模型加以运用，从而建构解决问题的方法体系.这样，学生头脑中能快速辨认、随时提取、简单和谐的基本图形分析法，自然流畅和快捷有效，由此成为学生的自然解法.

[1] 王尧兴.一个数学模型的中考情结[J].数学教学，2013(10)：37-41.

[2] 蔡卫兵.在基本图形的导航下进行合理思考[J].中学数学，2016(6)：51-55.

O123.1

A

1003-6407(2017)10-13-04