一道高考试题的解法探究及拓展
甘肃省定西市安定区东方红中学(743000) 付宏祥
一道高考试题的解法探究及拓展
甘肃省定西市安定区东方红中学(743000) 付宏祥
题目 (2017年全国II卷(12题))已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则的最小值是( )

平面向量具有代数和几何双重形式,其与诸多数学知识广泛联系,着重考查学生灵活运用知识解决数学问题的能力,是解决数学问题的重要工具.该题将向量与最值有机的结合起来,看似平淡,但剖析其内涵,挖掘其内在的功能,是一道值得我们深思探究的问题.
1 解法探究
探究1 利用平面向量的基本代数运算解决问题
平面向量的运算涉及模长与夹角两方面的关系,最值又涉及不等式的灵活运用,这就为问题解决增添了一定的难度,如何将两方面的知识综合运用,显得尤为重要.
解法一 如图1,以PB、PC为边作平行四边形PBDC,易知O为BC的中点,设∠APO=θ(0≤θ≤π),因为△ABC是边长为2的等边三角形,所以
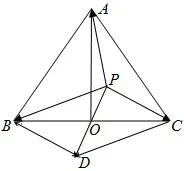
图1
由余弦定理及基本不等式知,
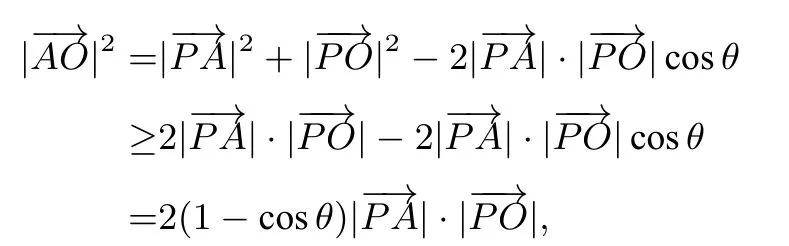
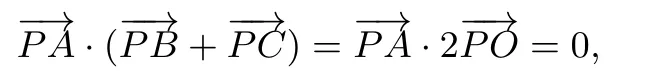
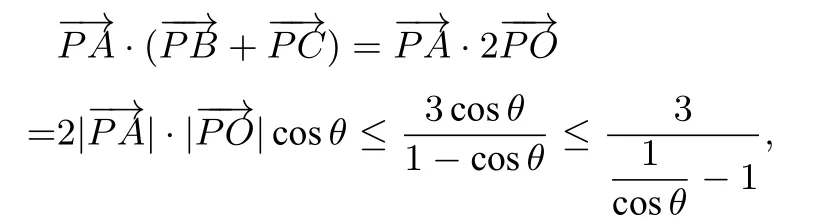
易知θ=π,即P为OA的中点时,有最小值.综上,的最小值是
评注 问题解决着眼于转化向量的数量积的计算问题,通过余弦定理及基本不等式使得问题解决的变量尽量减少起来,借助函数的最值求解方式解决问题.
探究2 利用平面向量的基本坐标运算解决问题
利用平面向量解决数学问题中,坐标法是一种快捷、高效的方法.通过建立平面向量直角坐标系,将所该问题转化为函数最值的求解,是行之有效的方法.
解法二 如图2,以BC为x轴,BC的中点O为坐标原点,建立直角坐标系O−xy,由△ABC是边长为2的等边三角形得

图2
设P(x,y),则所以,
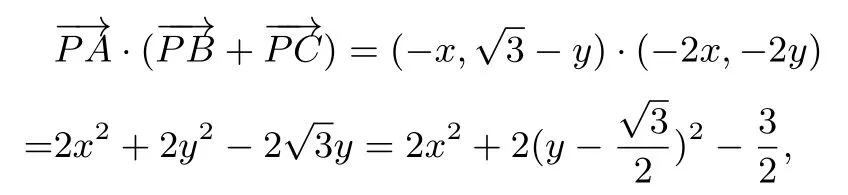
评注 问题解决利用直角坐标系中点的坐标化,使问题成为求解二元二次函数的最值问题,利用配方法寻求其最值,问题便迎刃而解.
2 问题拓展
2.1 将正三角形拓展到一般三角形中
结论 已知P为△ABC所在平面ABC内一点,AO为边BC的中线,则当P为AO的中点时,取得最小值.
证明 如图3,以BC为x轴,BC的中点O为坐标原点,建立直角坐标系O−xy,取A(b,c),B(−a,0),C(a,0),其中a>0,c/=0.
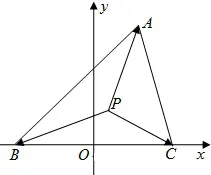
图3
设P(x,y),则所以,
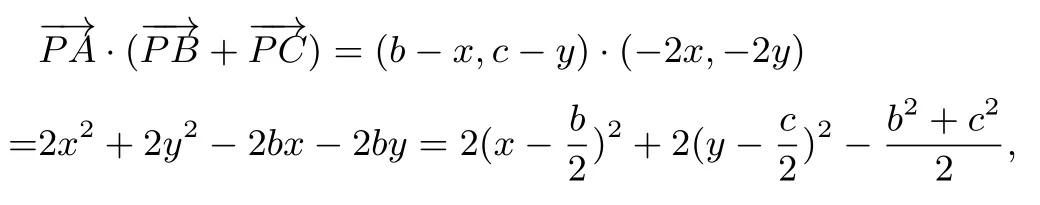
2.2 将正三角形拓展到正方形
结论 已知正方形ABCD的边长为a,P为平面ABCD内一点,则当P为正方形ABCD的中心时,取得最小值.
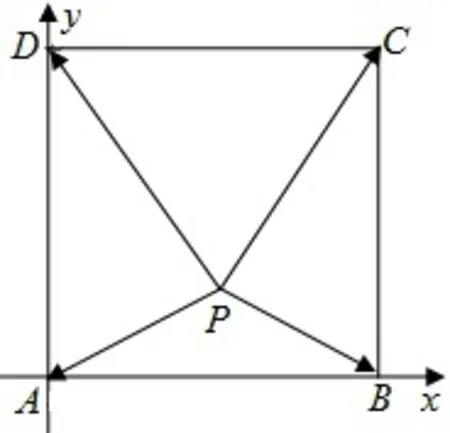
图4
证明 如图4,以AB为x轴,AD为y轴,建立直角坐标系A−xyz,取A(0,0),B(a,0),C(a,a),D(0,a).


