2017年高考数学应用问题趋势分析*

广州市第十六中学(510100) 温伙其

2017年高考数学应用问题趋势分析*

广州市第十六中学(510100) 温伙其

重视数学应用问题教育是新课程实施的重要标志,无论是数学课标、数学教材,还是高考数学试题,无不充分体现.迄今,涉及生产和生活实际的数学应用问题已经成为每年高考数学试卷的必考内容,旨在考核学生运用数学知识解决实际问题的基本素养,展现数学的科学价值和人文价值,发展学生数学建模素养和创新意识.因此,剖析提炼2017年各地高考数学应用问题的命题特点与命题趋势,有助于深化数学应用问题教学实践,提升学生解决数学应用问题的意识与能力.

1.2017年高考数学应用问题题型及内容分布

据统计,2017年全国高考数学试卷共14套,其中,全国I—III卷(文理),北京、山东、天津卷(文理),浙江、江苏卷(不分文理).这些试卷涉及的数学应用问题题型、分值、知识点等,具体分布如

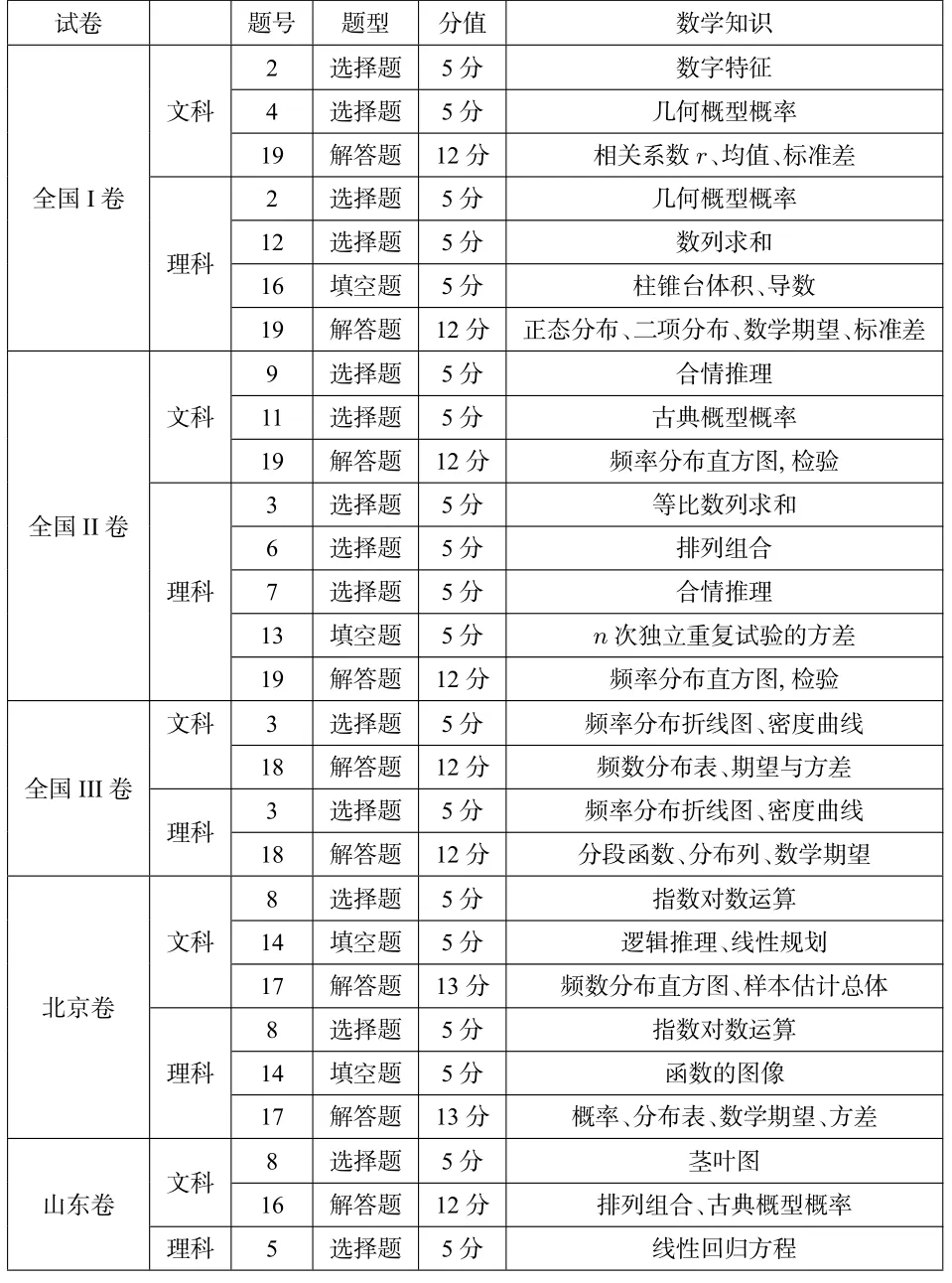
表1 2017年高考数学试卷中的数学应用问题分布

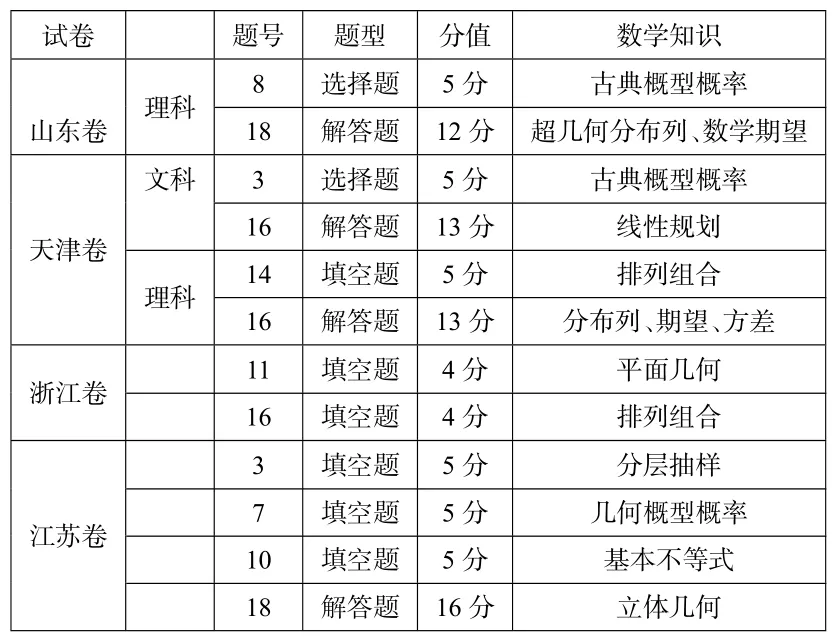
(接上表)2017年高考数学试卷中的数学应用问题分布

纵观表1,不难发现:

(1)从题型与分值看,无论是文理分卷、文理同卷,一般地,每份试卷设置1—2道客观题(选择题、填空题)和一道解答题(浙江卷只有2道填空题,江苏卷有3道选择题,全国I卷理科有3道客观题,全国III卷理科有4道客观题),每套试卷分值在8—32之间,占比5.33%—21.33%,解答题分值为12、13或 16.

(2)从数学内容与难度看,内容主要涉及概率统计、数列、排列组合、线性规划、基本不等式、平面几何、立体几何、函数及图象、逻辑推理等,其中,除江苏的立体几何解答题外,其他解答题均为概率统计问题,难度处于中等偏易.

(3)从背景看,选材紧密联系生产和生活实际,关注社会热点,加强对应用意识的培养和考查,力求解决生产问题.如经济领域:“销售酸奶利率”出现在全国理科III卷第18题,“购买货物使一年的总运费与总存储费用之和最小”出现在江苏卷第10题;生活领域:“连续剧播放时长、广告播放时长、收视人次”出现在天津文科卷第16题,“汽车经过十字路口遇到红灯”出现在天津理科卷第16题;农业领域:根据给定的指标,“来评估这种农作物亩产量稳定程度”出现在全国文科I卷第2题,“海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比”出现在全国理科II卷第18题;教育领域:“大学艺术专业学生参加某次测评”出现在北京文科卷第17题,“甲、乙、丙、丁四位同学询问成语竞赛的成绩”出现在全国理科II卷第9题;医疗领域:“研究新药的疗效,记录了两组患者的生理指标x和y的数据”出现在北京理科卷第17题;旅游领域:“旅游爱好者计划到亚洲国家和欧洲国家去旅游”出现在山东理科卷第10题,“为了解游客人数的变化规律,提高旅游服务质量”出现在全国文科III卷第3题;科研领域:“在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响”出现在山东理科卷第18题,“为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系”出现在山东理科卷第5题.

2.2017年高考数学应用问题的命题特点

2.1 立足基础知识,渗透数学文化的考查

《2017年普通高考数学考试大纲》修改部分,特别强调在高考中增加对数学文化的考查.今年的高考应用题,努力挖掘我国古代数学的精髓,选取体现中国古代优秀数学文化,并与中学数学内容紧密结合的素材编拟试题.在考查基础知识、基本思想方法的同时,引导考生深刻认识中华民族优秀传统文化的博大精深和源远流长,并予以传承.

例1 (全国理科I卷第2题)如图1,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )

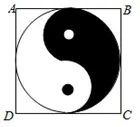
图1

结合数学文化中的太极图来考查几何概型符合考纲新增的要求.解题过程中引导学生发现图形的对称性,使学生进一步发展了几何直观能力,增强了运用图形解决问题的意识,提高了数形相结合的能力.本题不仅增加了对于数学文化的考查,还利用图形的对称性来分析问题,体现了高中数学核心素养中的直观想象.此题综合考查了学生的几何直观能力、分析能力和计算能力,是一道符合考纲的综合性好题.

例2(全国理科II卷第3题)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )

A.1盏 B.3盏 C.5盏 D.9盏

本题选自于我国明朝著名数学家程大位其名著《算法统宗》中记载数学问题的一首诗.学生通过阅读材料,既能感受古诗的美,又可了解古代数学文化.并对古诗提供的信息进行分析、判断和整理,提炼相关的数量关系,将问题转化为数学问题,构造出等比数列模型,知项数(七层)、公比(倍加增)、前n项和(共灯三百八十一)求a1(问尖头几盏灯).

除此以外,浙江卷第11题考查了古代数学家刘徽创立的“割圆术”估算圆周率π,北京理科卷第8题考查了围棋状态空间复杂度的上限,这些题目都散发着浓厚的数学文化气息,隐藏着丰富的数学知识,它们的解决需要学生的阅读能力、理解能力、运算能力、建模能力.

2.2 概率统计应用问题是高考数学的考查主干

再次纵观表1,主观题中,14套高考试卷中,除浙江卷外每套试卷的解答题中都有1道应用问题;而13套应用问题考查中,考查统计概率有12道(江苏卷的考查为立体几何),数量比重为92.3%;客观题中,共考查27道应用问题,考查统计概率有16道,数量比重为59.3%.概率统计是高考考核的重中之重,分值占应用题比例为76.4%.符合考纲对数据处理能力的要求:主要是考查运用概率统计的基本方法和思想解决实际问题的能力.

2.3 突出对图表信息等数据处理素养的考核

数学应用问题的呈现形式,不仅仅满足于文字语言和符号语言,相反,现在以丰富多样的各种图形语言出现.它要求学生识别图表,使用图表进行获取数据进行处理,这紧扣《2017年普通高考数学考试大纲》提出五种能力中的数据处理能力,即收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,并作出判断[1].如频率分布直方图出现于全国文科II卷第19题、全国理科II卷第18题、北京文科卷第18题;折线图出现于全国III卷第3题(文理相同);散点图出现于北京理科卷第14题、第17题;茎叶图出现于山东文科卷第8题;四棱柱出现于江苏卷第18题;同时大量的二维表格出现在题目中,这里不再一一列举.对于频率分布直方图、折线图、散点图即为平面直角坐标系类,应清晰横纵坐标的几何意义,变量互相之间的线性或函数关系.

3.高中数学应用问题教学的若干建议

3.1 重视图表法解高考数学应用问题的教学

现在的数学应用问题,条件较多,数量关系复杂,变量错综变化,用一般的方法解比较繁琐.图表法,它既符合《2017年普通高考数学考试大纲》提出空间想象能力的要求:会用图形与图表等手段形象揭示问题的本质[2];又有助于清晰解题思路,使复杂问题形象化,降低空间难度,达到去伪存真,化繁为简,化难为易的目的.下面以线性规划和逻辑推理来阐述列表法的操作和应用.

例3(天津文科卷第16题)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:

连续剧播放时长(分钟)广告播放时长(分钟)收视人次(万)甲705 60乙60 5 25

已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.

(I)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;

(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?

分析 由题意列表如下

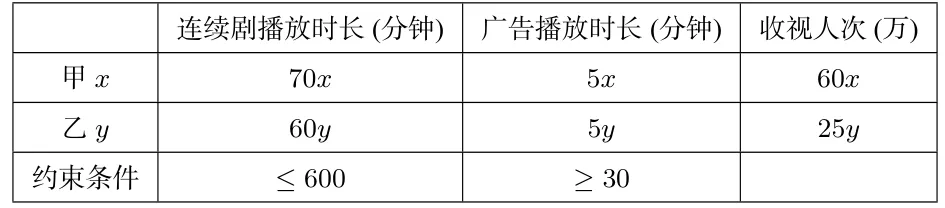
连续剧播放时长(分钟)广告播放时长(分钟)收视人次(万)甲x 70x 5x 60x乙y 60y 5y 25y约束条件≤600≥30

则约束条件为:

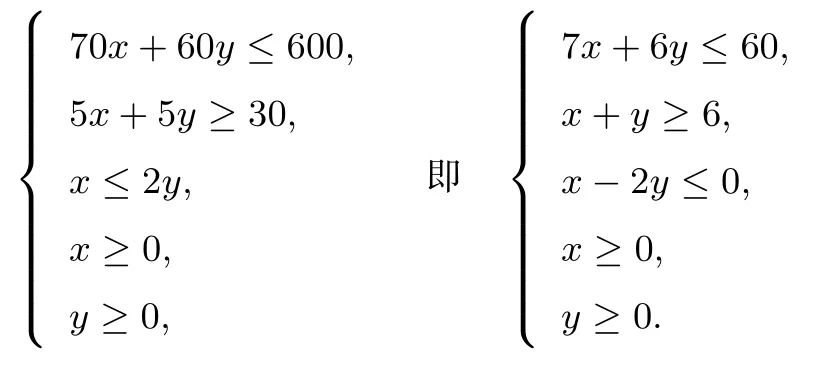
该二元一次不等式组所表示的平面区域如图2:

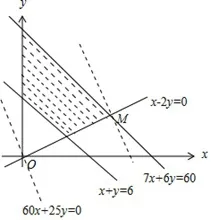
图2

设总收视人次为z万,则目标函数为z=60x+25y变形为画图2所以由图2可知,当直线z=60x+25y经过可行域上的点M时,截距最大,即z最大.解方程组得点M的坐标为(6,3).所以电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多.

一般地,线性规划问题的特点有两个变量,为了避免混淆,通过列出二维表格,方便理清各个量之间关系.题目每一个条件对应二维表格中的一行(一列),对应就是一个不等式,把所有不等式综合一起则为约束条件(不等式组),不等符号隐藏于“不多于”“不少于”等文字语言.而对目标函数的处理,先写出函数解析式,再转化为带几何意义的三种模型:截距型y=kx+z、截斜率型和距离型最后做出约束条件和目标函数的图象即可直观发现最值.

例4(全国理科II卷第7题)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )

A.乙可以知道四人的成绩

B.丁可以知道四人的成绩

C. 乙、丁可以知道对方的成绩

D. 乙、丁可以知道自己的成绩

分析 只要掌握关键:四人所知只有自己看到、老师所说及最后甲说话,题目即转化为以下四个事件

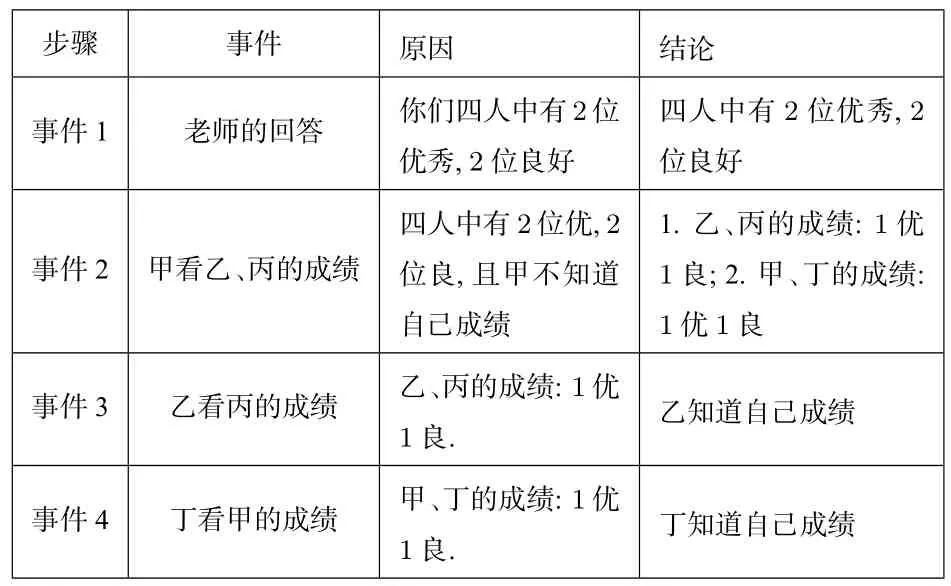
步骤事件原因结论事件1老师的回答你们四人中有2位优秀,2位良好四人中有2位优秀,2位良好事件2甲看乙、丙的成绩四人中有2位优,2位良,且甲不知道自己成绩1.乙、丙的成绩:1优1良;2.甲、丁的成绩:1优1良事件3乙看丙的成绩乙、丙的成绩:1优1良.乙知道自己成绩事件4丁看甲的成绩甲、丁的成绩:1优1良.丁知道自己成绩

故选D.

波利亚的《怎样解题》表提到“第一步:你必须弄清问题,未知数是什么?已知数据是什么?条件是什么?画张图,引入适当的符号;第二步:找出已知数与未知数之间的联系.”[3]列表法非常直观体现已知和未知,寻找量与量之间的联系;它还有利于把文字语言转化为符号语言,甚至可向图形语言迈进.本题考查逻辑推理,题干内容几乎都是文字语言.在推理过程中,每一步骤包含一个事件(数据),就是一行,隐藏一个原因(条件已知),可以推导一个结论(未知).

3.2 重视非统计概率型数学应用问题的教学

熟练解决应用问题的一般方法,优化解题的阅读、建模、解模、检验四个环节.把平时的课堂教学的重点放在如何提高学生的阅读能力即审题能力和怎样提升学生将实际问题转化为数学问题能力这两个关键点上.

例5 (2017北京理科卷第14题)三名工人加工同一种零件,他们在一天中的工作情况如图3所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.

图3

(1)记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是___.

(2)记pi为第i名工人在这一天中平均每小时加工的零件数,则p1,p2,p3中最大的是___.

分析 第一步,审题:掌握信息Ai表示第i名工人上午的工作时间和加工的零件数(已知);Bi表示第i名工人上午的工作时间和加工的零件数(已知);求一天加工的零件总数最多的工人(未知);求一天中平均每小时加工的零件数最多的工人(未知).

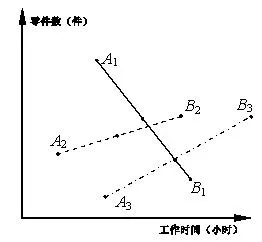
图4

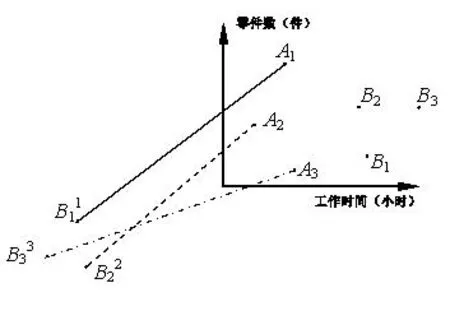
图5

[1]教育部考试中心.2017年普通高等学校招生全国统一考试大纲[M].北京:高等教育出版社,2016.

[2]教育部考试中心.2017年普通高等学校招生全国统一考试大纲[M].北京:高等教育出版社,2016.

[3][美]波利亚著,涂泓,冯承天译.怎样解题[M].上海:上海科技出版社,2011.

*本文系广州市越秀区教育科学“十三五”规划立项课题—基于视觉化表征高中数学应用问题的教学研究(课题批准号:越学科类[2016]08)和广州市越秀区科技工业和信息化局立项课题—基于视觉化表征高中数学应用问题的教学研究(课题批准号:软科学研究计划2016-JY-012)阶段性研究成果