由一道培训题引出抛物线的一组优美性质
福建漳州开发区厦门大学附属实验中学(363123) 林运来
由一道培训题引出抛物线的一组优美性质
福建漳州开发区厦门大学附属实验中学(363123) 林运来
题目 在直角坐标系xOy中,抛物线C的顶点是坐标原点O,准线方程:y=−1.
(1)求抛物线C的方程;
(2)过点P(2,−1)向抛物线C作切线,切点分别为A,B,求直线AB的方程;
(3)过点P(t,−1)(t∈R)向抛物线C作切线,切点分别为A,B,求△PAB面积的最小值.
此题是第28届“希望杯”高二年级的一道培训题,笔者对其进行深入研究,推导得出抛物线的一组优美性质,现介绍如下,供大家参考.
性质 在平面直角坐标系xOy中,抛物线C∶x2=2py(p>0)的焦点为过点P(t,s)(t,s∈R,且t2>2ps)向抛物线C作切线,切点分别为A(x1,y1),B(x2,y2)且直线PA,PB与x轴分别交于M,N两点.则
(1)抛物线C在点A处的切线PA的方程为x1x=p(y+y1);
(2)直线AB的方程为tx−py−ps=0;
(3)点A,P,B的横坐标成等差数列;
(4)三角形PAB的面积等于
(5)P,M,F,N四点共圆.
证明 (1)由x2=2py,得
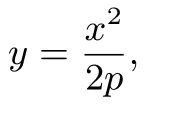
求导得

所以抛物线C在点A处的切线斜率为所以曲线C在点A处的切线方程为
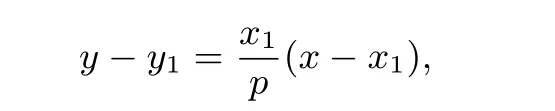
即
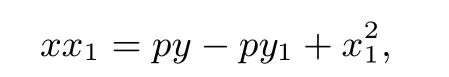
又因为=2py1,代入化简得x1x=p(y+y1).
(2)由(1)得,直线PA,PB的方程分别为
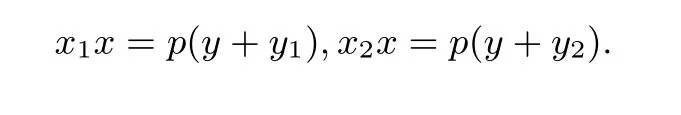
又因为直线PA,PB都经过点P(t,s),所以
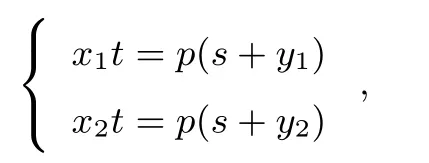
这表明A,B两点都在直线tx=p(s+y)上,所以直线AB的方程为tx−py−ps=0.
评注 由结论(2),不难得出如下的推论:当点P在抛物线C的准线上时,直线AB经过点F.反之,若直线AB经过抛物线C的焦点F,则点P在C的准线上.
(3)联立

消去y,整理得

由韦达定理,得

由①中的前一式知A,P,B三点的横坐标成等差数列.
(4)由上述①中的两式,可得
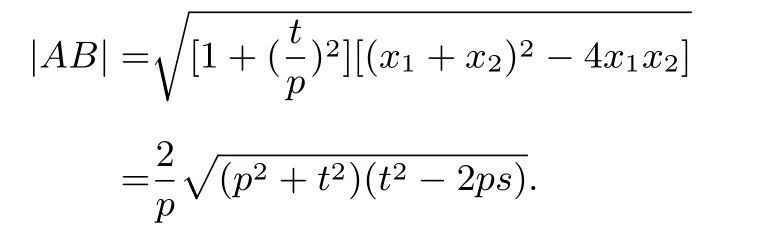
又因为点P到直线AB的距离所以

(5)因为直线PA的方程为x1x=p(y+y1),则所以

所以

即MF⊥PM,同理可得NF⊥PN.所以P,M,F,N四点在以线段PF为直径的圆上,即P,M,F,N四点共圆.

