一题五法 各显神通—一道2017年高考选择题的解法探究
广东省佛山市顺德区乐从中学 (528315) 林国红
一题五法 各显神通—一道2017年高考选择题的解法探究
广东省佛山市顺德区乐从中学 (528315) 林国红
题目再现:(2017年全国高考数学(理科I卷)第11题)设x,y,z为正数,且2x=3y=5z,则()
A.2x<3y<5zB.5z<2x<3y
C.3y<5z<2xD.3y<2x<5z
试题结构非常简单,题干也短,构思独特.主要考查指数函数、对数函数、幂函数性质及其相关运算,指数形式与对数形式的互化,还对于不等式的证明方法有较高的要求;考察学生逻辑思维能力、推理论证能力、运算及数据处理等能力.本文将给出此题的多种解法,抛砖引玉.
解法一(直接法)由2x=3y,两边平方可得,

所以2x>3y;由2x=5z,两边平方可得,

所以2x<5z;综上可得,3y<2x<5z.
评注 本解法通过两边平方后,利用幂函数与指数函数的单调性来证明,解法简单明了.
解法二(赋值法) 令x=1,则有2=3y,2=5z,可得

所以
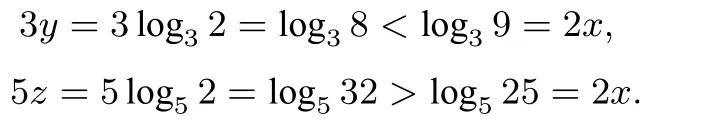
综上可得,3y<2x<5z.
评注 赋值法所体现的是从一般到特殊的转化思想,在高考题中屡见不鲜,赋值应以赋简单值为主.本解法之所以赋值,是想减少变量,达到简化目的;赋值后,再进行指对互化,利用对数函数的单调性来证明.
解法三(作差法) 因为x,y,z为正数,设2x=3y=5z=t(t>1),两边取自然对数,有

即
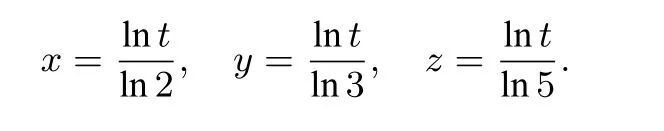
则有

因为

所以2x−3y>0,即2x>3y;同理可证2x<5z.综上可得,3y<2x<5z.
评注 作差法也是比较大小的常用方法,属于比较法的一种,是证明不等式的最基本方法.其步骤为:作差→变形→判断差的符号.变形是比较大小的关键,变形的目的在于判断差的符号,变形常用方法有通分、因式分解、配方等.本题的变形后还利用到对数函数的单调性.
解法四(作商法)因为x,y,z为正数,设2x=3y=5z=t(t>1),两边取自然对数,有
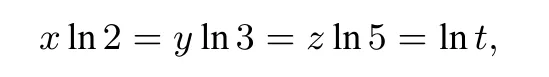
即
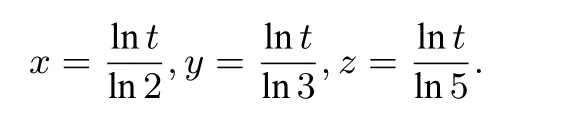
则有

ln9>ln8,所以即2x>3y;同理可证2x<5z.综上可得,3y<2x<5z.
评注 作商法是比较大小的常用方法,属于比较法的一种.其步骤为:作商→变形→判断商与1的大小.一般来说:当要证的式子两端是乘积的形式或幂、指数时可考虑此法.
解法五(构造函数法) 因为x,y,z为正数,设2x=3y=5z=t(t>1),两边取自然对数,有

即
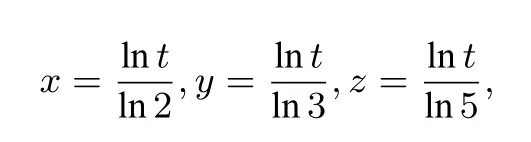
所以

考虑到2x,3y,5z式子的结构相同,可构造函数

又因为lnt是大于0的常数,所以只须考虑函数即可.由可得g(x)在(1,e)单调递减,在(e,+∞)单调递增,所以f(x)在(1,e)单调递减,在(e,+∞)单调递增.又因为e<3<4<5,所以f(3)<f(4)<f(5),故有

且有

即得
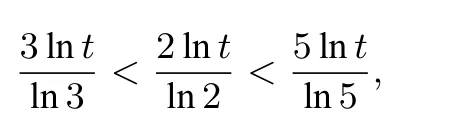
所以3y<2x<5z.
评注 构造函数法是证明不等式一个重要方法,其思路是发掘待证不等式的结构特征,合理变形,构造相应的函数,利用导数研究函数的单调性使不等式得以证明.
以上的几种解法,从不同的角度出发思考问题,各显神通,这充分体现数学高考题的不拘一格,一道试题往往考查多种能力、多种思想方法;同时,高考试题在命制时充分考虑到考生数学能力的个体差异,大多数试题的解答方法、思维方式不是唯一,一题多解,给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的.另外也说明高考要突出考查知识主干,贴切教学实际,扎实基础,重视数学的计算能力与思想方法,所以我们要在平时的学习与训练中重视知识的储备和方法的积累,才有可能缩短思维的长度,达到事半功倍的效果.
[1]人民教育出版社课程教材研究所.数学必修1[M].人民教育出版社A版,2007.
[2]人民教育出版社课程教材研究所.数学选修4-5[M].人民教育出版社A版,2007.
[3]周来友.一道课本习题的十种证法[J].高中数学教与学,2017(5)23-25.

