从不等式链的角度看一道高考解析几何试题的命制*

甘肃省兰州新区舟曲中学(730087) 李守明

从不等式链的角度看一道高考解析几何试题的命制*

甘肃省兰州新区舟曲中学(730087) 李守明

题目 (2017年全国卷II理科第10题)已知F为抛物线C∶y2=4x的焦点,过F做两条互相垂直的直线l1和l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为().

A.16 B.14 C.12 D.10

1.试题的两种解法

解法1 依题意,直线l1和l2的斜率存在,且斜率不为0,设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),又设直线l1的方程为y=k(x−1),代入抛物线方程y2=4x,消去y得,

则

所以

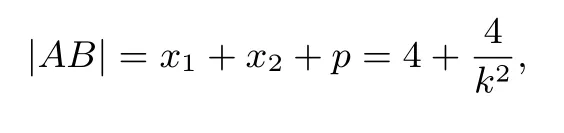
同理可得

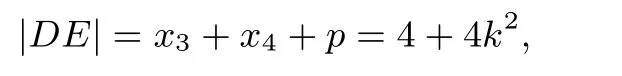
则

解法2 如图1所示,设AB倾斜角为θ,作AK1垂直准线,AK2垂直x轴,垂足分别为

所以|AF|cosθ+p=|AF|,

图1

同理可得

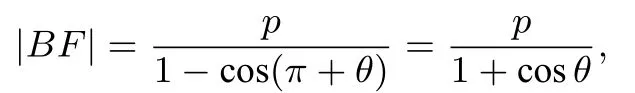
则

同理

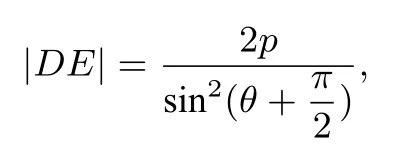
所以

评注 直线与圆锥曲线相交形成的弦中,焦点弦是较为特殊的,焦点弦长的计算也比较独特,较少运用弦长公式,而主要采用圆锥曲线的定义,解法1借助抛物线的定义,得到焦点在横坐标轴正半轴上的弦长公式|AB|=x1+x2+p,解法2同样是借助抛物线的定义,结合几何图形,得到焦点在横坐标轴正半轴上的弦长公式后续解答变得简单,解法1运用基本不等式,解法2运用三角函数的有关知识得到本题的解.

2.试题的产生思路

此题命题的思路是什么?又会有怎样的变式呢?联想到不等式链

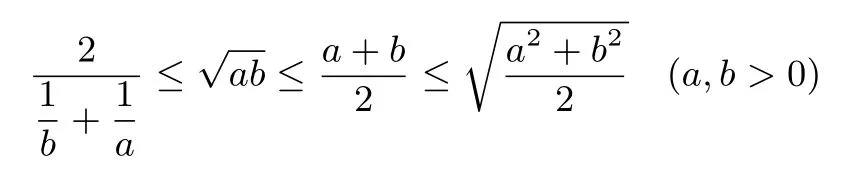
既然本题|AB|+|DE|有最小值,那么或者|AB|·|DE|就有可能为定值.笔者带着这种猜想进行了探索和证明.

变式1 已知F为抛物线C∶y2=4x的焦点,过F做两条互相垂直的直线l1和l2,直线l1与C交于A,B两点,直线l2与C交于D,E,则为定值.

证明 依题意,直线l1和l2的斜率存在,且斜率不为0,设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),又设直线l1的方程为y=k(x−1),代入抛物线方程y2=4x,消去y得,

则

所以

同理可得

所以

解法3

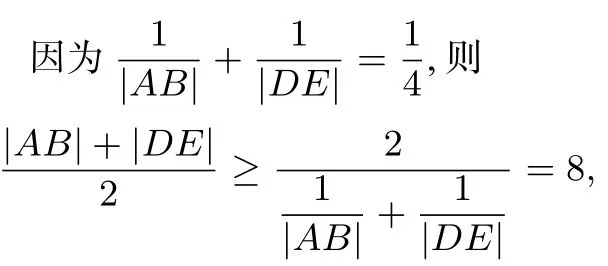
所以|AB|+|DE|≥16,当|AB|=|DE|时取等号.

3.结论的推广

在一般情形下的抛物线y2=2px(p＞0),AB和CD为过焦点且互相垂直的弦,那么是否也为定值呢?

推广1 已知F为抛物线y2=2px(p＞0)的焦点,过F做两条互相垂直的直线l1和l2,直线l1与C交于A,B两点,直线l2与C交于D,E,则为定值.

证明 以抛物线的焦点F为极点,x为极轴建立极坐标系,设点A(ρ,θ),则

其中p表示焦点到准线的距离,所以

同理可得

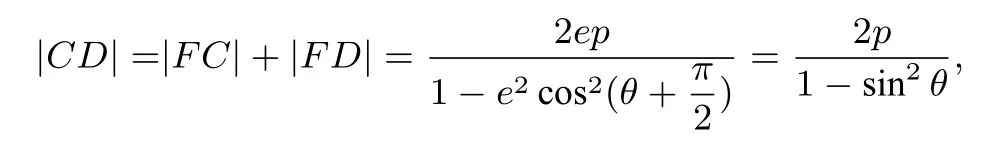
所以

那么对于圆锥曲线中的椭圆和双曲线来说是不是也有相类似的结论呢?

证明 不妨设F为椭圆的左焦点,以F为极点,x为极轴建立极坐标系,设点A(ρ,θ),则

其中p表示焦点到准线的距离,所以

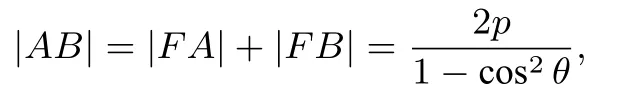
同理可得

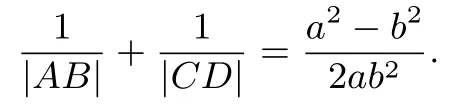
当A,B在双曲线同一支,而C,D不在双曲线的同一支时,

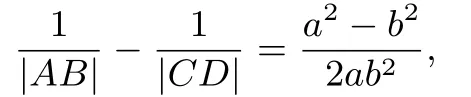
当A,B不在双曲线同一支,而C,D也不在双曲线的同一支时,

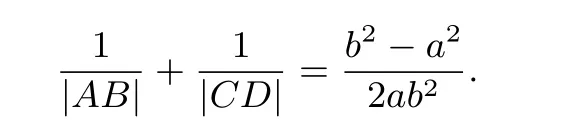
证明 不妨设F为双曲线的右焦点,以F为极点,x为极轴建立极坐标系,设点A(ρ,θ),当A,B,C,D在双曲线的同一支上时,则

其中p表示焦点到准线的距离,所以

同理可得

所以

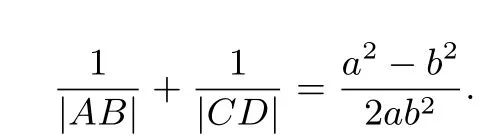
当A,B在双曲线同一支,而C,D不在双曲线的同一支时,

当A,B不在双曲线同一支,而C,D也不在双曲线的同一支时,则有

4.高考链接

例 (2007年高考全国卷I文第22题理21题)已知椭圆的左右焦点分别为F1,F2过F1的直线交椭圆于B,D两点,过F2的直线交椭圆于A,C两点,且AC⊥BD,垂足为P.

(I)P点的坐标为,证明

(II)求四边形ABCD的面积的最小值.

解 (I)略;(II)因为

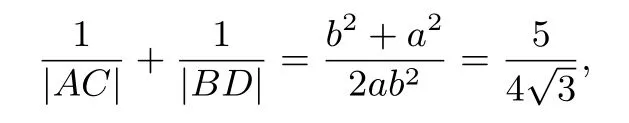
则

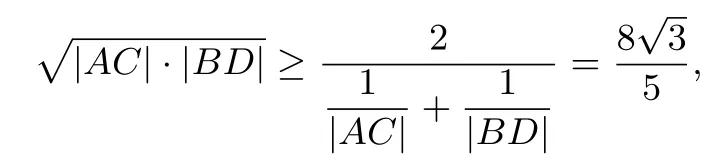
当且仅当|AC|=|BD|取等号.

5.追本溯源

从不等式链的角度命制试题,在人教版选修课本习题中有所体现,原题如下:

(人教A版选修4-4第15页)已知椭圆中心为O,长轴、短轴的长分别为2a,2b(a＞b＞c),分别为椭圆上的两点,且OA⊥OB.

(2)求△OAB面积的最大值最小值.

(2)因为

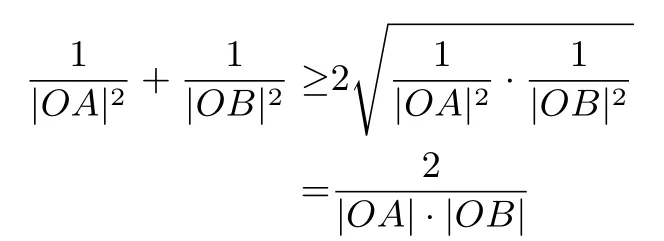
|OA|=|OB|取等号.则

所以

故求得△OAB面积的最大值为本题可用椭圆的参数方程求得的求△OAB面积的最大值为.

6.变式练习

以抛物线为例,明白了焦点弦AB和CD互相垂直时,具有性质为定值,那么就可以理解试题命制者命题的初衷,借助不等式链,改编形成不同的试题.

例 (2017四川资阳市模拟试题)过抛物线C∶y2=4x的焦点F做互相垂直的弦AC和BD,则点A,B,C,D构成四边形的面积的最小值为( )

A.16 B.32 C.48 D.64

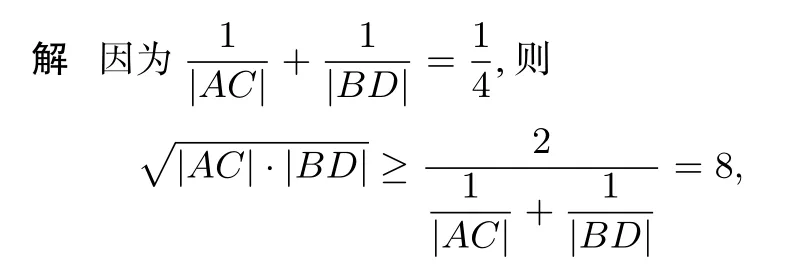
(当且仅当|AC|=|BD|取“=”),

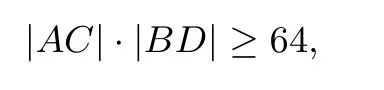
所以

当且仅当|AC|=|BD|取等号.

解 因为

所以

当|AB|=|CD|时取等号.所以或a=(舍),则故答案为D.

[1]普通高中课程标准实验教科书选修4-4[M],北京:高等教育出版社,2007.

兰州市“十三五”教育科学规划课题《运用“一题一课”培养高中学生数学解题能力的研究》