一类带有混合噪声的非线性随机时滞系统鲁棒L1控制
李艳辉 李星蒴 张永丰
(1.东北石油大学电气信息工程学院;2.大庆油田有限责任公司第二采油厂规划设计研究所)
一类带有混合噪声的非线性随机时滞系统鲁棒L1控制
李艳辉1李星蒴1张永丰2
(1.东北石油大学电气信息工程学院;2.大庆油田有限责任公司第二采油厂规划设计研究所)
针对一类带有混合噪声的非线性连续不确定随机时滞系统,研究了鲁棒L1控制器的设计问题。通过构造时滞依赖的Lyapunov函数,利用积分不等式方法,建立系统在均方意义下渐近有界的充分条件,并在此基础上设计控制器,使闭环系统均方渐近有界且输出峰值小于给定的L1性能指标γ。基于LMI技术,将鲁棒L1控制问题转化为凸优化问题,并通过一组线性矩阵不等式予以解决。最后,通过数值仿真验证了所设计控制器的有效性。
随机时滞系统 混合噪声 鲁棒L1控制器 非线性
持续干扰一直是工业生产中不可避免的一大难题,如化工过程中进口流量的持续波动,输电系统的耦合干扰及电磁干扰等。持续干扰轻则影响产品质量,重则使系统失稳甚至造成生产事故。对于此类问题,鲁棒L1控制作为一种抑制持续干扰的有效方法逐渐成为研究热点。鲁棒L1控制方法的目的在于设计一个控制器,使得系统不仅满足稳定性能,而且在持续幅值有界干扰下依然能够获得峰值-峰值增益的最小上界。由于持续干扰在实际系统中普遍存在,因此鲁棒L1控制得到了广泛的研究和应用[1,2]。文献[3]提出一类基于T-S模型的网络控制系统,研究了鲁棒L1控制问题,并给出了一种动态输出反馈控制器的设计方法。文献[4]基于倒立摆系统给出了一种L1/H∞滤波器的设计方法。但这些成果只是考虑了系统的外界扰动,而忽略了系统内部存在的随机噪声现象。
随机噪声分为乘性噪声和加性噪声。前者一般由信道不理想导致,与系统状态为乘积关系,即噪声随状态收敛为零而衰减,目前对于这类噪声的研究较为多见[5,6];后者一般由系统自身结构不理想(如热噪声、散粒噪声等)导致,与系统状态呈加性关系,因此该噪声不依赖于系统状态而独立存在。文献[7]利用Bellman随机动态规划法推导了两类噪声的LQ最优控制算法,并通过解代数黎卡提方程的方法得出了相应的控制器。文献[8]基于带有两类噪声的随机系统设计了干扰观测器,通过前馈控制方法给出了系统均方渐近有界的充分条件。综上,在混合两类噪声的情况下研究随机系统的鲁棒L1控制问题具有十分重要的意义。
在此,笔者研究了一类非线性不确定随机时滞系统在混合噪声情况下的鲁棒L1控制问题。通过状态反馈控制器使闭环系统均方意义下渐近有界,同时满足鲁棒L1性能的干扰抑制水平。最后,用数值仿真验证结论的有效性。
1 问题描述
考虑如下随机时滞不确定系统:
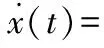
(D+ΔD)x(t)ξ1(t)+D1ξ2(t)
(1)
y(t)=Cx(t)
x(t)=φ(t),∀t∈[-ρ,0]
其中,x(t)∈Rn为状态变量,u(t)∈Rm为控制输入,v(t)∈Rp为干扰输入,y(t)∈Rq为控制输出,φ(t)为[-ρ,0]范围内的初始函数,ξ1(t)、ξ2(t)分别为乘性和加性白噪声,f(x(t),t)为非线性函数,f(0,t)=0,且满足:
fT(x(t),t)f(x(t),t)≤cxT(t)x(t)
(2)

[ΔAΔA1ΔDΔB]=GΓ(t)[H1H2HDHB]
(3)
其中,G、H1、H2、HD、HB为已知常数矩阵,Γ(t)为未知时变矩阵,且满足:
ΓT(t)Γ(t)≤I∀t
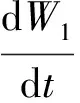
dx(t)=(A+ΔA)x(t)dt+(A1+ΔA1)x(t-τ(t))dt+(B+ΔB)u(t)dt+Bvv(t)dt+
F0f(x(t),t)dt+(D+ΔD)x(t)dW1+D1dW2
(4)
y(t)=Cx(t)
x(t)=φ(t),∀t∈[-ρ,0]
其中,W1(t)和W2(t)为相互独立的标准维纳过程,满足E[dW(t)]=0,E[d2W(t)]=dt,E[·]为数学期望。
为实现控制目的,笔者设计了如下状态反馈控制器:
u(t)=Kx(t)
(5)
其中,K为待设计的控制器参数。
考虑上述控制器,构造闭环系统:
dx(t)=(A+BK+ΔA+ΔBK)x(t)dt+(A1+ΔA1)x(t-τ(t))dt+Bvv(t)dt+
F0f(x(t),t)dt+(D+ΔD)x(t)dW1+D1dW2
(6)
y(t)=Cx(t)
x(t)=φ(t),∀t∈[-ρ,0]
引理1[8]假设存在函数V(t)、κ∈Kv∈K∞和正数p、β、σ,对于(x(t),t)∈Rn×R+使得:
κ(|x|p)≤V(x,t)V(x,t)≤-σV(x,t)+β
(x(t),t)∈Rn×R+满足:
则系统是p阶均方渐近有界。
引理2[4]设Φ是给定的对称矩阵,H和G为适当维数矩阵,那么对于所有满足ΓT(t)Γ(t)≤I的矩阵函数Γ(t),有下述不等式成立:
Φ+GΓ(t)H+HTΓT(t)GT<0
成立的充要条件是存在一个标量ε>0,使得:
Φ+εGGT+ε-1HTH<0
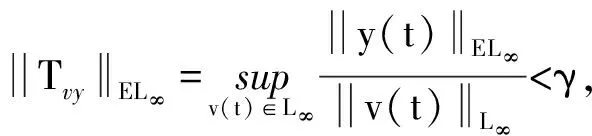
满足以上条件的控制器被称为鲁棒L1控制器。
2 L1性能指标分析
定理1 考虑闭环系统(6),给定标量α>0、β>0、c>0、h>0,若存在正定矩阵P∈Rn×n、Q∈Rn×n、R∈Rn×n和正数ε1∈R,满足下列线性矩阵不等式:
(7)
αQ-(1-αh)R<0
(8)
(9)
(10)
Ω11=PA+ATP+PBK+KTBTP+PΔA+ΔATP+PΔBK+KTΔBTP+
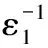
则闭环系统均方渐近有界且满足L1扰动抑制水平γ。
证明设P>0、Q>0、R>0,选取Lyapunov-Krasovskii泛函为:
V(t)=V1(t)+V2(t)+V3(t)
V1(t)=xT(t)Px(t)
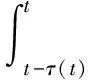

根据伊藤公式,得:
V≤ηT(t)Φη(t)+Tr[PD1]-xT(s)Rx(s)ds
(11)
ηT(t)=[xT(t) xT(t-τ(t)) vT(t)]
Ω=PA+ATP+PBK+KTBTP+PΔA+ΔATP+PΔBK+KTΔBTP+
进一步变换可得:
V≤ηT(t)Πη(t)+Tr[D1TPD1]-xT(s)Rx(s)ds-αxT(t)Px(t)+αvT(t)v(t)
(12)
存在以下不等式:
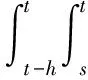
考虑式(8)、(12),则有:
V≤ηT(t)Πη(t)+Tr[PD1]-αV(t)+αvT(t)v(t)
(13)
V≤Tr[PD1]-αV(t)+αvT(t)v(t)
(14)
V≤αvT(t)v(t)-αV(t)+β
(15)
设p=2,κ(|x|p)=λmin(P)|x|2,σ=α,根据引理1,当v(t)=0时,系统为均方渐近有界。
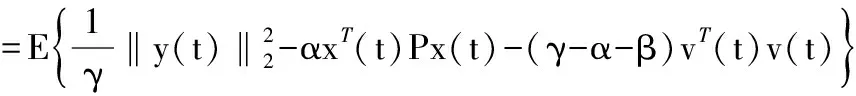
(16)
根据式(9)和Schur补定理可知,m(t)<0,则有:
E{yT(t)y(t)} (17) 在定理1的基础上,笔者进一步给出了鲁棒L1控制器的求解方法,并以线性矩阵不等式的形式给出了其参数化表示形式。 定理2 考虑闭环系统(6),给定标量α>0、β>0、δ>0、h>0,若存在正定矩阵X∈Rn×n、M∈Rn×n、N∈Rn×n和标量ε1∈R、ε2∈R、ε3∈R使如下不等式成立,则闭环系统(6)为均方渐近有界且满足干扰抑制水平为γ的L1性能: (18) αM-(1-αh)N<0 (19) (20) (21) 证明在定理1成立的基础上,经过分离不确定项和应用Schur补引理,式(7)可等价为: (22) 对式(22)进行全等变换,左右乘对角阵diag(P-1,P-1,I,I,I,I,I),定义变量X=P-1,M=P-1QP-1,N=P-1RP-1,Y=KX,δ=c-1,则式(22)可化简为: (23) 由此可以得到状态反馈控制器的参数矩阵K=YX-1。同理,对式(8)、(9)两边分别左右乘X、矩阵diag(X,I,I)及其转置,则定理2得证。 考虑闭环系统(6),其相关参数为: 取利普希茨常数c=1,通过对α线性搜索得到参数α=0.4,在非线性函数f(x(t),t)=sin(t)x(t)的基础上,根据定理2可得干扰抑制度γ=0.9066,则所求控制器为: u(t)=[-13.1032 -36.6474]x(t) 选取初始状态x(0)=[-1 2],设峰值有界的外部干扰v(t)=sin(t),通过数值仿真分别得到开环和闭环系统的输出信号y(t)响应曲线如图1所示。可以看出,开环系统(无控制器)输出曲线是发散的,而带有鲁棒L1控制器的闭环系统输出曲线是收敛的,且满足给定的L1干扰抑制水平,表明笔者设计的控制器是有效的。 图1 开环/闭环系统的输出响应曲线 针对一类带有混合噪声的非线性随机时滞系统,通过Lyapunov稳定性理论、LMI技术和积分不等式,研究了该系统的鲁棒L1控制问题。所设计的鲁棒L1控制器能够保证所研究系统均方意义下渐近有界,且满足指定的L1噪声抑制水平。仿真结果证明,笔者设计的状态反馈控制器是有效的。 [1] He S,Liu F.Robust Peak-to-Peak Filtering for Markov Jump Systems[J].Signal Processing,2010,90(2):513~522. [2] Hasegawa T,Yamaguchi R,Nagasaki M,et al.Inference of Gene Regulatory Networks Incorporating Multi-Source Biological Knowledge via a State Space Model withL1Regularization[J].Plos One,2014,9(8):e105942. [3] 李艳辉,周秀杰,刘俊丽.基于T-S模糊模型的不确定时滞系统鲁棒L1滤波[J].控制与决策,2016,31(5):895~900. [4] 齐迹,李艳辉.倒立摆扰动系统的L1/H∞滤波器设计[J].控制工程,2016,23(8):1267~1271. [5] George J.A Robust Estimator for Stochastic Systems under Unknown Persistent Excitation[J].Automatica,2016,63(s1): 156~161. [6] Liu L,Li X,Wang H,et al.Global Asymptotic Stabilization of Stochastic Feedforward Nonlinear Systems with Input Time-delay[J].Nonlinear Dynamics,2016,83(3):1503~1510. [7] 伍友利,方洋旺,王洪强,等.乘性加性噪声Markov跳变系统线性均方最优控制[J].空军工程大学学报(自然科学版),2009, 10(5):32~36. [8] Wei X J,Wu Z J,Karimi H R.Disturbance Observer-based Disturbance Attenuation Control for a Class of Stochastic Systems[J].Automatica,2016,63(s1):21~25. [9] Yue D,Han Q L.Delayed Feedback Control of Uncertain Systems with Time-varying Input Delay[J].Automatica,2005, 41(2):233~240. RobustL1ControllerforNonlinearStochasticTime-delaySystemwithMixedNoises LI Yan-hui1, LI Xing-shuo1, ZHANG Yong-feng2 TH865 A 1000-3932(2017)07-0619-06 2017-01-13, 2017-05-02) (Continued on Page 647) 国家自然科学基金项目(61673102);中国高等教育机构博士基金项目(20132322120003);黑龙江省博士后科学研究发展基金项目(LBH-Q13177);黑龙江省自然科学基金项目(F201403);东北石油大学培育基金项目(XN2014112)。 李艳辉(1970-),教授,从事鲁棒控制、滤波和智能控制的研究,LY_hui@hotmail.com。
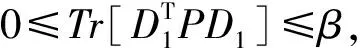
3 鲁棒L1控制器设计

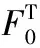
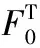
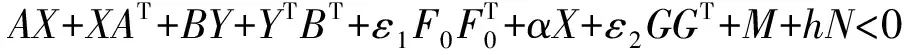
4 数值分析
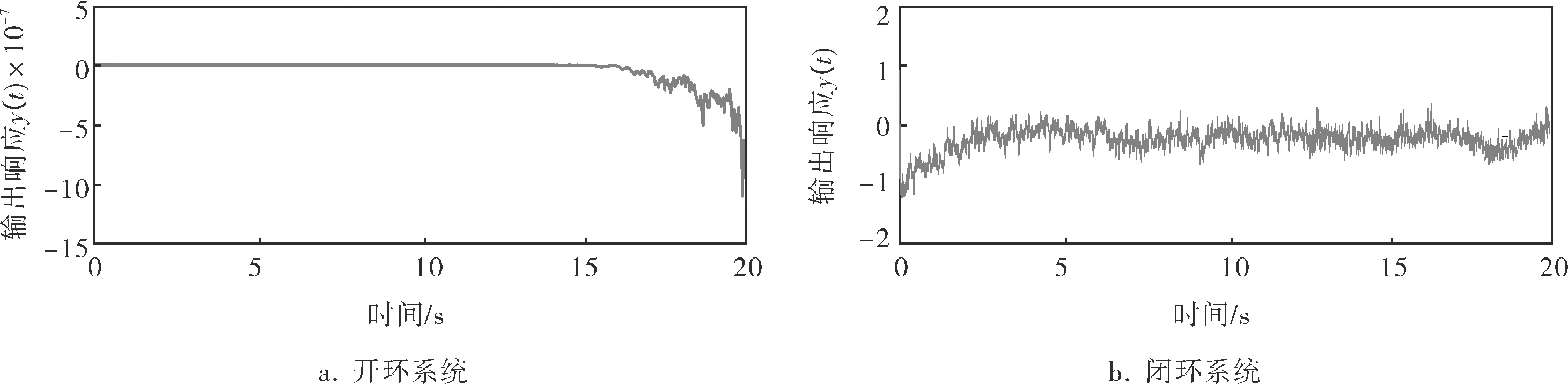
5 结束语

