加热炉炉温的模糊广义预测控制仿真研究

薛美盛 刘 波 孟 俊 杨 猛 秦宇海

(1.中国科学技术大学信息科学技术学院；2.江苏庞景节能科技有限公司)

加热炉炉温的模糊广义预测控制仿真研究

薛美盛1刘 波1孟 俊1杨 猛1秦宇海2

(1.中国科学技术大学信息科学技术学院；2.江苏庞景节能科技有限公司)

针对加热炉炉温的大惯性、大滞后及非线性等特点，提出一种基于T-S模糊模型的模糊广义预测控制策略。T-S模糊模型的前件和后件参数分别采用粒子群优化的模糊C-均值算法和递推最小二乘法辨识，根据输入变量更新模型隶属度并将T-S模糊模型等价转换为线性模型，以此作为预测模型应用于广义预测控制。仿真结果表明：该方法在不同工况下均具有较短的调节时间，在扰动作用下有很强的鲁棒性。

模糊广义预测控制 加热炉炉温 T-S模糊模型

加热炉是轧钢生产线的主要能耗设备，其控制目标是在获得满足轧机开轧所要求的钢坯温度分布的前提下，实现最小的钢坯表面烧损和能耗经济指标[1,2]。加热炉本质上是一个大惯性、大滞后且多变量的非线性系统，当炉内工况发生变化或出现大的扰动时，模型参数将会发生变化。预测控制算法具有工程背景强、设计简单及鲁棒性强等特点，在过程控制领域应用广泛[3]。而Takagi-Sugeon(T-S)模糊模型[4]本质是一种非线性模型，在工业过程系统的建模与控制中优势明显。将模糊模型作为非线性预测控制的预测模型已经成为研究热点。模糊预测控制已经有许多研究成果[5～8]，张化光等提出了模糊广义预测控制算法[5]；邢宗义等提出一种新的基于T-S模型多步线性化的模糊预测控制策略，并用pH中和过程的仿真验证了该方法的有效性[6]；而彭玉凤和王辉已将该控制策略应用于pH中和过程[7]。模糊C-值聚类(Fuzzy C-Means，FCM)算法常用于T-S模糊模型结构的划分，以避免多变量带来的“维数灾难”[9,10]。但FCM对初始值敏感且易于陷入局部最优，为解决上述问题，王纵虎等将初始聚类中心和模糊加权指数同时进行粒子群优化搜索[11]，宋娇和葛临东将采用遗传算法得到的聚类中心作为FCM聚类算法的初值，其仿真结果证明了算法的有效性[12]。

为改善加热炉炉温预测控制中模型失配的问题，提升控制品质，笔者提出加热炉炉温的模糊预测控制策略。

1 加热炉炉温的模糊预测控制策略

加热炉炉温的模糊预测控制策略控制框图如图1所示，控制器采用广义预测控制(Generalize Predictive Control，GPC)，预测模型选择T-S模糊模型，前件结构和参数采用PSO-FCM辨识，后件参数采用递推最小二乘法辨识。

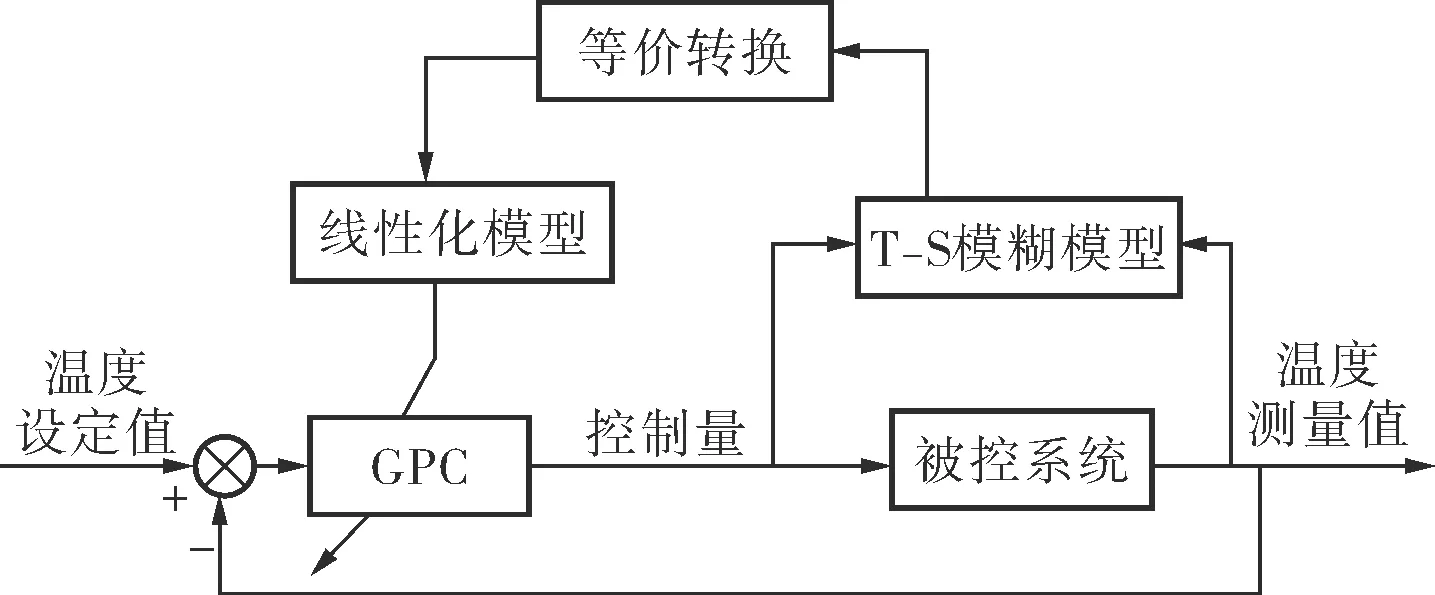
图1 模糊预测控制策略控制框图

2 模糊广义预测控制器的设计

2.1 T-S模糊模型辨识

2.1.1 模型定义

T-S模糊模型的本质是一种非线性模型，易于表达复杂系统的动态特性，其结论采用线性方程式描述。此处T-S模糊模型由N条规则组成，规则形式描述为：

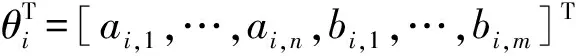
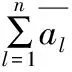
(1)

对于小样本问题，可以找到N条模糊推理规则，保证一个规则对应一个输入输出数据对。但是对于大样本问题，为了避免模糊规则的“维数灾难”，先用模糊聚类算法对样本数据进行分组，再将每一组数据视为一个数据对进行模糊建模。此处的T-S模糊模型前件中采用数据集代替单个变量，后件采用线性方程形式，相应的模糊规则等价为：

Ri:ifx∈Cithenyi=fi(x)

x=(x1,x2,…,xd)

其中Ci为输入空间分割后的部分空间。这样输入变量的隶属度函数不能像直接划分法那样独立地给出，但可以利用模糊聚类求得条件部分输入变量的联合隶属度函数。前件结构和参数用PSO-FCM算法辨识得到，后件参数用最小二乘法辨识。

2.1.2基于PSO的FCM

FCM算法是一种基于目标函数的聚类算法，其目标函数为：

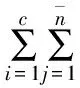
(2)

(3)

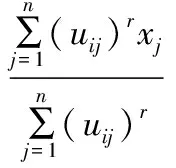
(4)

考虑到加热炉流量数据存在干扰，而FCM聚类结果对初始值和噪声数据敏感，容易陷入局部最优，所以笔者采用基于PSO的FCM对数据集进行聚类。PSO算法是一种基于种群全局搜索的自适应进化算法，初始化一群随机粒子，通过迭代找到最优解。在每一次迭代中，粒子通过跟踪各自的最优值和种群最优值来寻求最优解，在找到这两个最优值后，通过以下公式更新自己的速度和位置：

(5)

(6)

其中，xi表示粒子当前的位置；vi表示粒子当前的速度；pi表示粒子到达过的最好位置；pg表示当前的全局最优点；r1、r2是属于(0，1)的随机数；c1、c2是学习因子；i=1,2,…,M表示粒子数；n=1,2,…,S表示粒子维数。将目标函数(2)作为PSO的适应度函数，FCM中聚类中心迭代式(3)由PSO速度和位置迭代式(5)、(6)替代即可得到基于PSO的FCM。

基于加热炉输入输出数据对的T-S模糊模型的完整辨识步骤如下：

a. 数据的选择和预处理。从历史数据中选择能反映被控对象各种工况的数据，使用相关分析结合专家知识选取输入变量，对输入输出数据进行滤波并做归一化处理。

b. 初始化PSO相关参数，包括种群数M，最大迭代次数J，惯性权重因子η，微粒群的初始位置和速度，全局最优位置；FCM中以所有聚类中心坐标构造聚类中心集X=(x1,x2,…,xN)作为PSO的一个粒子，目标函数(2)作为适应度函数，根据速度和位置更新式(5)、(6)进行全局寻优，然后利用FCM算法中的隶属度函数计算式(3)计算每一簇中输入向量的隶属度。

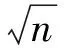
d. 递推最小二乘法辨识后件参数。

至此，T-S模糊模型参数全部辨识得到。方程式(1)中的各项系数是时变参数，但是在采样周期内假设每条规则的联合隶属度不变，可以等价转换为受控自回归积分滑动平均模型(CARIMA)[13]。

2.2 广义预测控制器

广义预测控制采用CARIMA模型，当C(q-1)=1时其增量模型如下：

A(q-1)Δy(t)=B(q-1)Δu(t-k)+ζ(t)

其中y(t)、u(t)和ζ(t)分别为系统的输出、输入和零均值白噪声；q-1为后移算子，且有差分算子Δ=1-q-1；k表示系统最小时延。且有：

A(q-1)=1+a1q-1+a2q-2+…+anaq-na

B(q-1)=b0+b1q-1+b2q-2+…+bnbq-nb

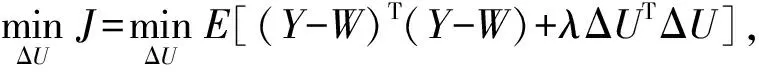
3 仿真

唐山某带钢厂，钢坯从推钢口进入加热炉，以煤气为燃料经一加热段、二加热段和均热段加热至钢坯要求的轧制温度后由出钢口送往轧线。其中二加热段作为主要加热段，温度和流量变化范围广，控制难度大，所以此处重点研究二加热段。基于CARIMA模型的GPC已在现场投运，但正常工作时会因为工作点变化致使模型失配导致炉温升降不及时，为此笔者提出将炉温GPC中的CARIMA模型用非线性T-S模糊模型替代。

此处T-S模糊模型基于加热炉历史数据建立，煤气流量是影响炉温的最主要因素，选择煤气流量为输入变量，炉温为输出变量，建模原始数据共7 200组，相关性分析得系统滞后时间180s，采样间隔20s，数据预处理后共340组数据。FCM算法中模糊加权指数r=2，粒子群体M=20，最大迭代次数J=50，学习因子c1=c2=2，惯性权重ηmax=0.9、ηmin=0.4，模糊规则选择范围[2,20]，由聚类有效性指标得到的模糊规则数c=2，聚类中心V=[0.8264,0.8032；0.2774,0.2656]，辨识得T-S模糊模型为：

R1: ifX∈A1theny(k)=0.0804u(k-10)+0.9161y(k-1)

R2: ifX∈A2theny(k)=0.1245u(k-10)+0.9190y(k-1)

其中X=[u(k-10),y(k-1)]为输入变量；A为模糊划分，其联合隶属度由式(3)计算可得。T-S模糊模型辨识结果如图2a所示，误差曲线如图2b所示。

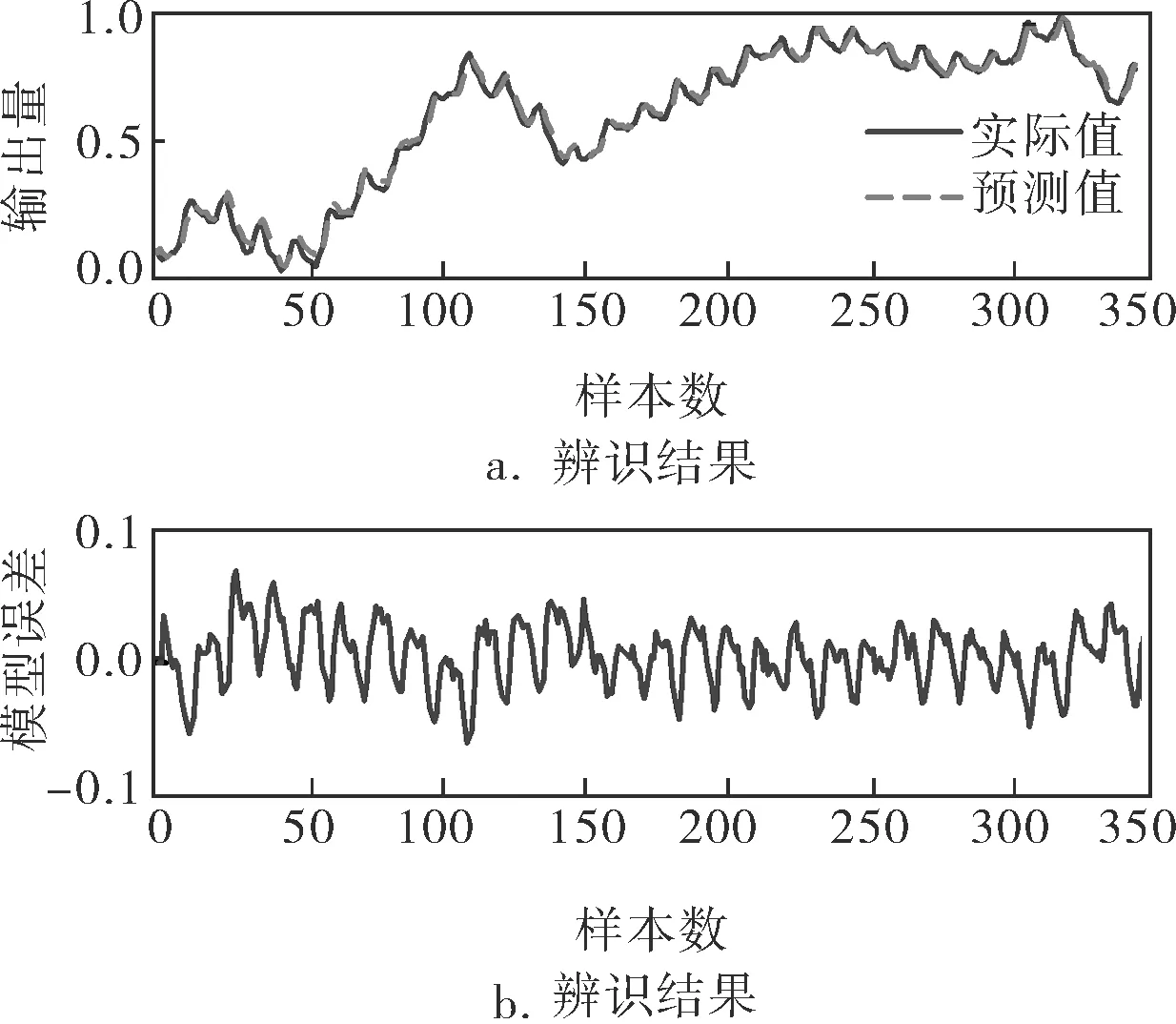
图2 T-S模糊模型辨识

用同样的数据集辨识CARIMA模型y(k)=0.0807u(k-10)+0.9208y(k-1)。

系统模型选用T-S模糊模型。GPC中预测步长P=60，控制步长Pu=15，柔化因子α=0.9，控制量变化量权重λ=4。假设在每一个采样时刻联合隶属度函数保持不变，根据文献[11]将T-S模糊模型等价转换为线性模型并用于GPC，并与基于CARIMA模型的GPC仿真结果进行对比(图3)。仿真中设定值阶跃变化对应实际加热炉的实际炉况，结合实际情况，分别在第4 000、7 000、11 000、14 000s加入8%的干扰以验证算法的鲁棒性。

仿真结果表明，T-S模糊模型对加热炉加热过程有很好的逼近特性；基于T-S模糊模型的GPC在不同设定值下均有较快的上升时间、调节时间和有较小的超调量，在扰动作用下均能很快跟踪到设定值，具有很强的鲁棒性。而基于CARIMA模型的GPC在设定值0.5以上时响应速度快、调节时间短且鲁棒性强，但设定值在0.5以下时响应曲线超调量大、调节时间长且抗干扰能力弱，出现模型失配的概率较大。

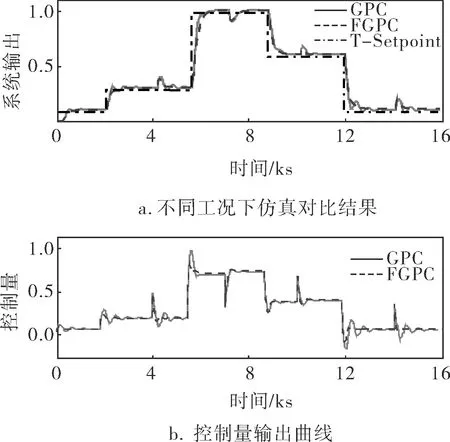
图3 两种控制策略仿真结果

4 结束语

为了提升加热炉的炉温控制品质，提出基于T-S模糊模型的GPC控制策略，T-S模糊模型根据加热炉历史数据集，前件采用PSO-FCM辨识，提升了聚类效果，后件参数采用递推最小二乘法辨识。仿真结果证实T-S模糊模型对加热过程有很好的逼近特性。由于该模型无需考虑对象的具体结构，通用性强，易于和预测控制结合，故将T-S模糊模型作为GPC的预测模型，并与基于CARIMA模型的GPC做仿真对比，结果表明前者在不同的工况下均具有较快的上升时间、较短的调节时间和较强的鲁棒性。仿真结果对实际应用有一定的指导意义。

[1] 荣莉,柴天佑,钱晓龙.加热炉过程控制技术的新策略——智能控制[J].控制与决策,2000,15(3):269～273.

[2] 唐桂华,庄正宁.炼油厂加热炉节能方案分析[J].化工机械,2000,27(6):352～355.

[3] 薛美盛,袁鑫,薛生辉,等.溶解氧的广义预测控制仿真研究[J].化工自动化及仪表,2016,43(4):359～362.

[4] Takagi T,Sugeno M.Fuzzy Identification of Systems and Its Applications to Modeling and Control[J].IEEE Transactions on Systems,Man,and Cybernetics,1985,SMC-15(1):116～132.

[5] 张化光,吕剑虹,陈来九.模糊广义预测控制及其应用[J].自动化学报,1993,19(1):9～17.

[6] 邢宗义,胡维礼,贾利民.基于T-S模型的模糊预测控制研究[J].控制与决策,2005,20(5):495～499.

[7] 彭玉凤,王辉.模糊预测控制在pH中和过程中的应用[J].控制工程,2006,(z1):61～64,157.

[8] Rastegar S,Araújo R,Mendes J,et al.Self-adaptive Takagi-Sugeno Model Identification Methodology for Industrial Control Processes[C].IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society.Piscataway,NJ:IEEE,2014:281～287.

[9] 薛美盛,孙胜杰,袁鑫,等.一种基于历史数据的加热炉温度模糊控制规则提取方法[J].化工自动化及仪表,2016,43(9):940～944.

[10] Pang L,Xiao K,Liang A,et al.A Improved Clustering Analysis Method Based on Fuzzy C-means Algorithm by Adding PSO Algorithm[C].International Conference on Hybrid Artificial Intelligence Systems.Berlin:Springer Berlin Heidelberg,2012:231～242.

[11] 王纵虎,刘志镜,陈东辉.基于粒子群优化的模糊C-均值聚类算法研究[J].计算机科学,2012,39(9):166～169.

[12] 宋娇,葛临东.一种遗传模糊聚类算法及其应用[J].计算机应用,2008,28(5):1197～1199.

[13] 张化光,何希勤.模糊自适应控制理论及其应用[M].北京:北京航空航天大学出版社,2002.

SimulationStudyofFuzzyGeneralizedPredictiveControlforReheatingFurnaceTemperature

XUE Mei-sheng1, LIU Bo1, MENG Jun1, YANG Meng1, QIN Yu-hai2
(1.CollegeofElectronicsScienceandTechnology,UniversityofScienceandTechnologyofChina; 2.JiangsuPanvieoEnergySavingTechnologyCo.,Ltd.)

TH862+.6

A

1000-3932(2017)07-0624-05

2017-01-20,

2017-04-24)

(Continued on Page 642)

薛美盛(1969-)，副教授，从事工业自动控制的研究。

联系人刘波(1990-)，硕士研究生，从事过程控制与优化的研究，boliu@mail.ustc.edu.cn。