基于蓄电池储能的直流微网惯性控制

任亚钊 于 明

(1.国网电动汽车服务有限公司；2.北京林业大学工学院)

基于蓄电池储能的直流微网惯性控制

任亚钊1于 明2

(1.国网电动汽车服务有限公司；2.北京林业大学工学院)

为提高直流微网抗干扰能力，改善系统暂态运行特性，提出了一种基于自适应下垂系数的储能变流器惯性控制方法。基于Matlab/Simulink仿真平台对所提方法进行了对比仿真分析，结果表明：在该控制策略下，直流微网具有较强的抗扰动能力，储能单元能够及时进行功率补给避免了负荷减载，系统供电可靠性和运行稳定性得到了提高。

惯性控制 直流微网 蓄电池储能 自适应下垂系数

近年来，微网的提出增加了分布式能源消纳的灵活性与稳定性。在各种形式的微网中，基于电力电子变流器并网的直流微网，因其高效性、灵活性及不存在交流系统频率与功角稳定性等问题而备受关注[1]。尽管储能元件的配置在一定程度上能够降低新能源波动性对系统的不利影响，然而对于本身为小惯性系统的直流微网而言，扰动下功率和直流电压的波动不可避免。因此，提高系统运行稳定性，满足负荷对高质量电能的需求成为亟待解决的问题。

目前，许多学者围绕微网中储能单元控制方案的选取开展了大量研究[2,3]，如采用基于直流电压偏差的比例积分控制方法进行储能电流调节，但难以避免调节的滞后性。而对提高系统惯性方法的研究仅限于通过超级电容来增加等效惯性，缺乏对系统运行经济性的考量[4,5]。因此，笔者通过改进微网中的储能单元控制方案，将反映系统功率状态的直流电压变化趋势引入储能单元控制，使储能系统具有对直流电压快速响应的特性，抑制系统扰动，达到提高微网惯性和运行稳定性的目的。

1 直流微网基本控制方法

1.1 典型结构

图1为直流微网的典型结构——简单的辐射型拓扑。其中，分布式电源采用永磁风电机组，通过相应的变流器W-VSC并入直流网络，为系统提供绿色能源。采用能量密度较大的蓄电池作为储能元件，经变流器Bi-DC与直流侧进行双向能量交换，达到平抑功率波动的目的。并网单元通过变流器G-VSC与主网间实现能量双向传输，在系统联网运行时，既能消纳直流侧富余功率，又能补充微网能量缺口。此外，系统中交流与直流负荷分别通过变流器L-VSC和L-DC实现并网。图1中，PWTi、PB、PG、PDC_L、PAC_L分别表示第i(i=1，…，n)个风电系统输出功率、储能单元输出功率、交流电网提供功率、系统内直流负荷和交流负荷；Udc_WTi、Udc_B、Udc_G、Udc_L1、Udc_L2分别表示第i个风电单元直流侧电压、储能、并网单元直流侧电压、直流负荷与交流负荷直流侧电压。

1.2 基于直流电压的微网分散控制方法

直流微网协调控制方法一般分为集中控制、分散控制与分布式控制3种。集中控制通过中央控制器和通信网络实现多种复杂控制目标，使系统运行经济、高效。但多种目标的实现影响了该方法的实时性，且单点通信故障会导致控制系统崩溃。分布式控制在通信延时和存在测量误差的状态下，系统稳定裕度、收敛速度等性能较差。由于基于直流电压的分散控制方法简单高效、易于功率协调控制且具备即插即用的特性，因而在微网控制中应用广泛。

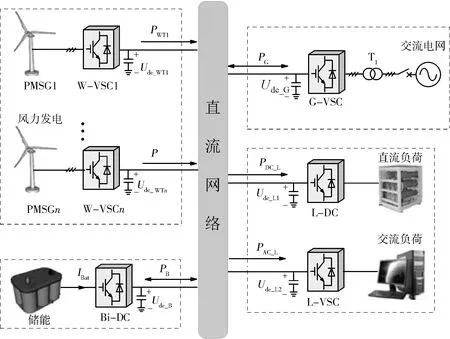
图1 直流微网的典型结构

在分散控制方法中，各单元依据直流电压数值确定相应控制模式。在联网运行状态下，当直流电压偏离额定值小于设定切换阈值时，由交流主网通过并网变流器维持微网功率平衡；当联网变流器输出到达极限值或系统故障导致输出功率受限时，联网单元输出功率为固定值，储能单元切换至直流电压控制模式以维持电压稳定；当风电系统输出功率较大而系统轻载时，将导致直流电压抬升至高限切换阈值，此时需对风电系统进行降功率控制；而当系统功率严重缺失、直流电压下降至低限切换阈值时，为保障重要负荷供电不中断，需按照预设优先级对负荷进行减载调节以稳定系统直流电压。图2为基于直流电压的微网分散协调控制曲线[1]。

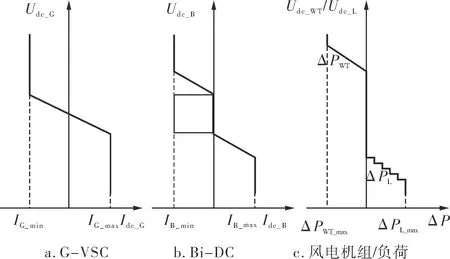
图2 基于直流电压的微网分散协调控制曲线

然而在分散控制方法中，控制模式切换阈值的选取会对系统的控制性能产生较大影响。较大的切换阈值带宽会降低系统控制精度，造成直流电压偏差增大；而较小的切换阈值间隔则有可能导致系统模式频繁切换，引起直流电压波动。提高系统等效惯性是降低直流电压偏差、抑制功率波动的有效方法。对于本质小惯性的直流微网系统，既可以采用超级电容器为系统提供快速功率支撑，也可以采用控制手段增加系统等效惯性。相比之下，前者经济性较差，因此，对储能系统控制策略进行改进以提高系统惯性、降低系统功率波动不失为一种两全的方法。

2 储能变流器控制方法

2.1 拓扑结构

直流微网中，双向储能变流器Bi-DC采用图3所示的拓扑结构，可工作于Boost模式或Buck模式，开关V1与V2互补运行。当直流微网存在功率缺口且无法完全依靠联网单元得到补充时，直流微网电压降低至相应控制模式切换阈值，储能单元向系统释放功率，维持直流侧功率平衡，双向变流器Bi-DC处于Boost工作模式；反之，当系统功率富余时，储能单元将暂存多余功率，储能变流器切换至Buck运行模式[6]。

图3 双向储能变流器Bi-DC拓扑结构

2.2 基本控制方法

如图4所示，当双向储能变流器Bi-DC工作于Boost模式时， V1一直维持截止状态。假设变流器开关周期为Ts，在开关V2导通期间(Ton)，蓄电池经V2构成回路将能量存储于电感L中；而V2关断期间(Toff)，L中存储的电磁能经二极管D1馈送至直流侧。因此，直流侧电压可通过调节开关V2的占空比DBoost与相应工作周期来控制。

图4 Boost工作模式

当变流器处于Boost工作模式时，开关管V2导通与关断时的回路方程为：

(1)

由于Ton=DBoostTs，Toff=(1-DBoost)Ts，则可以得到单个开关周期内电压平均值方程：

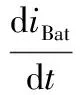
(2)

式中UBat、iBat——蓄电池电压、电流；

Udc_B——储能变流器直流母线电压。

由式(2)可知，当变流器工作在Boost模式时，通过调节占空比DBoost即可对蓄电池的放电电流进行控制，从而维持直流电压稳定。占空比DBoost的计算式为：

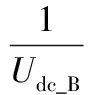
(3)

当储能变流器处于放电工况时，其控制结构如图5所示。其中，外环为直流电压控制，实现直流电压跟踪反馈调节；内环为电流控制，采用比例积分调节以消除电流稳态误差，且其参考值由外环输出给定。

图5 蓄电池放电时储能变流器的控制结构

如图6所示，当双向储能变流器Bi-DC工作于Buck模式时，V2一直维持截止状态。在开关V1导通期间(Ton)，蓄电池两端电压低于直流电压Udc_B，微网富余功率经电感L对蓄电池充电；在V1关断期间(Toff)，L存储的电磁能通过二极管D2续流，对蓄电池继续充电。因此，调节开关V1的占空比DBuck与工作周期便可以控制充电电流，进而调节直流电压。

图6 Buck工作模式

当变流器处于Buck工作模式时，开关管V1导通和关断期间的回路方程为：

(4)

由于Ton=DBuckTs，Toff=(1-DBuck)Ts，则可以得到单个开关周期内电压平均值方程：

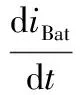
(5)

由式(5)可知，通过调整占空比DBuck即可实现蓄电池充电电流的调节。占空比DBuck的计算式为：

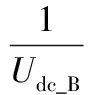
(6)

当储能变流器Bi-DC运行于Buck模式时，仍采用双闭环控制，其结构如图7所示。

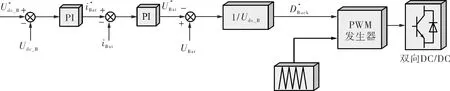
图7 蓄电池充电时储能变流器的控制结构

2.3 改进的惯性控制方法

在直流微网中，系统快速功率扰动直接表现为直流母线电压的快速变化。上述控制方法中外环采用固定的下垂系数，控制响应无法反映系统功率状态，导致控制相对滞后，直流电压调节效果不佳。直流电压Udc_B的计算式为：

(7)

式中ki——下垂系数；

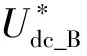
为使储能单元对微网扰动做出快速响应，对系统提供惯性支撑，以保持直流电压稳定，笔者提出了微网储能惯性控制策略。在该控制策略中，将储能单元变流器的下垂系数ki与直流电压变化率进行关联。当直流电压变化率大于设定参考阈值，即系统受到快速功率扰动时，采用自适应下垂系数，以增强储能单元响应速率，快速调整直流电压，为系统提供惯性支撑。自适应下垂系数的计算式为：

(8)

其中，kn_i为变流器固定下垂系数，m1、m2为与变流器额定容量、最大允许偏差等有关的常量。由式(8)可知，当系统电压变化率大于设定参考阈值C时，下垂系数进行自适应调整。m1可由下式求得：

(9)

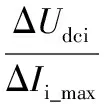
(10)

其中，ki_min为最小下垂系数；ΔUdci为储能变流单元最大电流(ΔIi_max)所对应的电压变化量，用于设置变流单元出口直流电压偏差允许值。由式(9)可知，m1的值取决于电压变化速率最大值|dUdc/dt|max和代表变流单元输出能力的ki_min。

当采用笔者所提出的自适应下垂系数惯性控制方法时，储能单元内环电流参考值的生成如图8所示。其中，Cj表示第j个变流单元的直流电压变化参考阈值。当微网处于稳定运行状态时，系统电压平稳且其变化率未达到设定参考阈值，经比较器运算输出数值0，即采用预设固定下垂系数；而当较大系统扰动引起快速电压变化，且大于设定参考阈值时，比较器切换输出至1，变流单元下垂系数进行自适应调整，迅速调节功率输出，避免直流电压扰动，为系统提供惯性支撑。随着扰动的减小，变流单元惯性响应能力随着m1的减小而减弱。

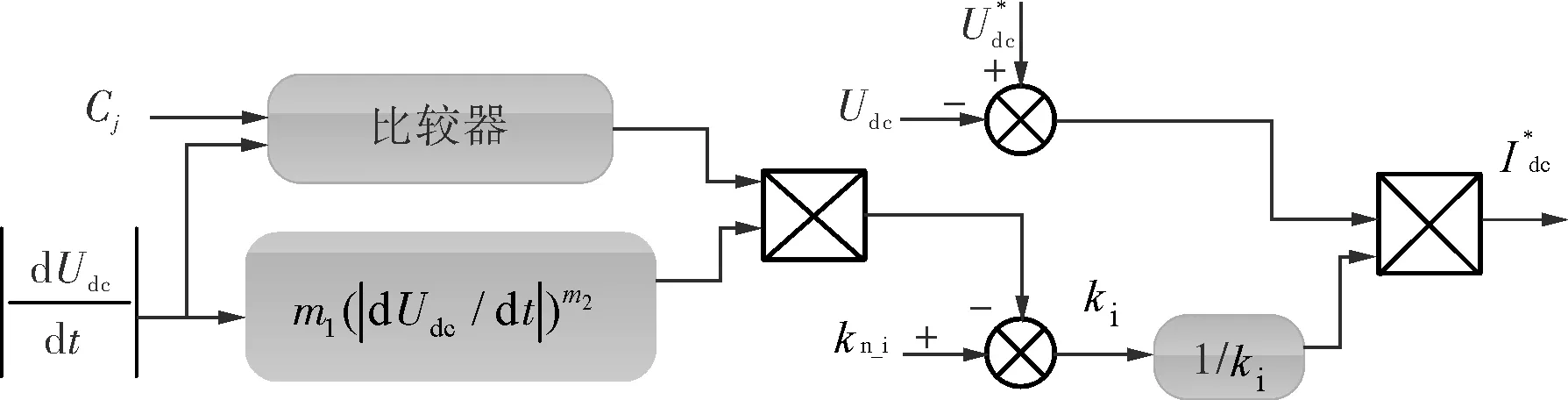
图8 自适应惯性下垂控制方法原理

3 仿真分析

3.1 仿真系统

为验证笔者所提出的储能单元惯性控制方法对系统的功率支撑作用，基于Matlab/Simulink仿真系统建立了含蓄电池储能的新能源直流微网仿真模型，其参数如下：

风电单元额定容量PWN50kW

联网单元额定容量PGN50kW

储能单元额定容量PBN50kW

直流母线额定电压UdcN400V

电网频率f50Hz

采样时间Tsp50μs

在交流主网故障、联网变流器限流运行的情况下，对比分析采用传统固定下垂系数与调节惯性的自适应下垂系数时，储能变流器的运行输出特性和对直流电压的调节效果。

3.2 暂时性孤岛工况仿真分析

仿真前5s，系统处于稳定运行工况，风电单元、蓄电池储能单元和交流电网向微网输出功率，保障负荷平稳供电。仿真第5s，交流侧发生故障致使联网变流器进行闭锁控制，直流微网暂时处于孤岛运行状态。

暂时孤岛运行时系统仿真特性如图9所示，可以看出，当不采用自适应下垂系数的惯性控制策略时，由于微网突陷孤岛运行模式，功率骤降，储能单元无法实现快速功率补给，导致直流电压迅速降低至368V。该电压数值已达到微网控制模式切换阈值，按照系统分散控制原理，系统将对非重要负荷进行减载，直至电压重新提升至反向电压参考阈值。而采用笔者所提出的控制策略时，在系统功率突降瞬间，较大的直流电压变化率触发惯性控制单元，储能变流器采用与直流电压变化相适应的下垂系数，在原功率输出的基础上增加了惯性功率输出，及时补偿了系统功率缺口，因而减小了直流电压的扰动，使之维持在380V左右，避免了甩负荷工况的发生，保障了供电的可靠性，提升了微网运行的稳定性。

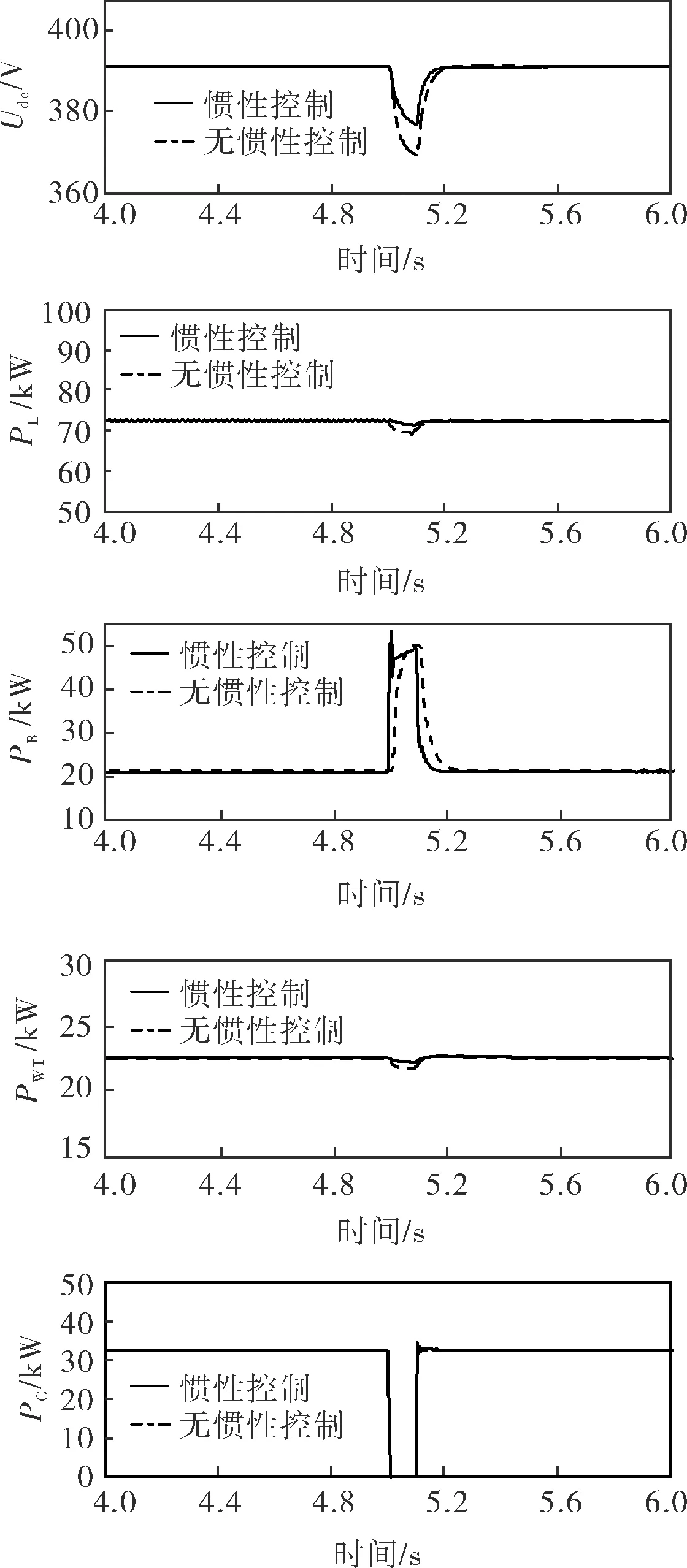
图9 暂时孤岛运行时系统仿真特性

4 结束语

笔者提出了一种直流微网蓄电池储能系统惯性控制策略。在该控制策略中，储能单元变流器下垂系数不再为固定值，而是与直流电压扰动相适应的可变参数。由于改进的下垂系统能够间接反映系统功率扰动状态，为微网提供及时高效的功率补给，因而避免了直流电压的大幅变动，提高了系统的有效惯性。通过Matlab仿真分析验证了所提控制策略的有效性，在系统暂时孤岛运行时，该控制策略能够为直流电压提供惯性支撑，避免了负荷减载运行，保障了直流系统的供电稳定性。

[1] 王毅,于明,李永刚.基于模型预测控制方法的风电直流微网集散控制[J].电工技术学报,2016,31(21):57～66.

[2] Ahmadi R,Ferdowsi M.Improving the Performance of a Line Regulating Converter in a Converter-Dominated DC Microgrid System[J].IEEE Transactions on Smart Grid,2014,5(5):2553～2563.

[3] Majumder R.Some Aspects of Stability in Microgrids[J].IEEE Transactions on Power Systems,2013,28(3):3243～3252.

[4] Braid J.Conceptual Design of a Liquid-Based Variable Inertia Flywheel for Microgrid Applications[C].IEEE International Energy Conference.Piscataway,NJ:IEEE,2014:1291～1296.

[5] Inthamoussou F A,Pegueroles-Queralt J,Bianchi F D.Control of a Supercapacitor Energy Storage System for Microgrid Applications[J].IEEE Transactions on Energy Conversion,2013,28(3):690～697.

[6] 张丽荣.风电直流微网的控制与保护技术研究[D].北京:华北电力大学,2015.

InertiaControlofDCMicrogridBasedonBatteryEnergyStorage

REN Ya-zhao1, YU Ming2
(1.StateGridElectricVehicleServiceCo.,Ltd.; 2.CollegeofEngineering,BeijingUniversityofForestry)

In order to enhance DC microgrid’s anti-interference ability and improve transient operation characteristics of the system, an inertia control method for the energy storage converter based on adaptive droop coefficient was proposed. Having Matlab/Simulink simulation platform based to compare and analyze the method proposed shows that, under the proposed control strategy, the DC microgrid has strong anti-disturbance ability and the energy storage unit supplies the power timely and the system’s service ability and operation stability can be improved.

inertia control, DC microgrid, battery storage, adaptive droop coefficient

TH862+.78

A

1000-3932(2017)07-0656-06

2017-02-24，

2017-05-16)

任亚钊(1986-)，工程师，从事新能源电动汽车的相关工作。

联系人于明(1987-)，博士研究生，从事新能源并网和直流微网的相关工作，ming_yu1987@163.com。