“三数”求解大揭秘
陈 刚
“三数”求解大揭秘
陈 刚
通过学习,我们知道“三数”指平均数、中位数、众数,分别反映了数据的平均水平、居中水平、集中水平,是人们对数据分析后做出合理决策的依据.确定一组数据的“三数”是中考的必考内容,根据它们各自的不同含义,其确定方法也不一样.同时,掌握其中的数学思想,更能助力同学们在数学的大海上远航.
方法篇
一、公式“算”出平均数
平均数是“算”出来的.由于n个数据x1,x2,…,xn的平均数x与每个数据大小都有关,因此,确定一组数据的平均数需要通过公式x1+x2+…+xn)进行计算.
例1 下表是对某学校男子足球队队员的年龄统计,则他们的平均年龄是____.
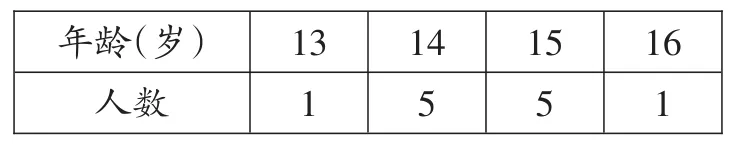
【解析】根据平均数的求法,用所有年龄的和除以总人数即可.
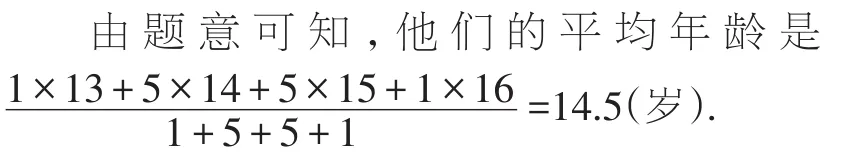
【点评】此题主要考查了平均数的求法,相对简单,细心计算即可得出答案.要注意当一组数据中有较多数重复出现时,应用加权平均数公式计算.
二、大小“排”出中位数
中位数是“排”出来的.由于一组数据的中位数与最大、最小的数据无关,因此确定一组数据的中位数只要将这组数据按照顺序(由小到大或由大到小)排列.此时,位于最中间的数据若只有一个,则该数即为这组数据的中位数;若有两个,则中位数是这两个数据的平均数.
例2 佳和中学生物兴趣小组调查了本地区几棵古树的生长时间,记录数据如下(单位:年):200,220,240,210,200,这组数据的中位数是____.
【解析】将这5个数按由小到大的顺序排列为:200,200,210,220,240,处于最中间位置的是210,所以这组数据的中位数是210.
【点评】确定n个数据的中位数时,先按大小将各数据依次排列,然后确定位于最中间的一个或两个数据.当n为奇数时,最中间一个数是第个;当n为偶数时,最中间两个数分别是第和第(+1)个.
三、抛头露面“数”众数
众数是“数”出来的.由于众数是指某组数据中出现次数最多的数,所以确定众数时,只要数一数每个数据出现的次数,保留出现次数最多的数即可.
例3 数据1,6,8,5,8,6,0的众数是____.【解析】该组数据中0、1、5均出现一次,6、
8均出现两次.
由于6、8出现次数最多,所以该组数据的众数是6和8.
【点评】确定众数时要注意两点:①不要错将数据出现的次数当成众数;②众数有时不止一个,不要数漏.
思想篇
一、方程思想
例1 一组数据4、x、5、10、11的平均数为7,则这组数据的众数是 .
【解析】由题意得4+x+5+10+11=7×5,解得x=5,所以这组数据为4、5、5、10、11,其众数为5.
二、整体思想
例2 有从小到大依次排列的9个数,其平均数为30,若其前5个数的平均数为20,后5个数的平均数为41,试求这组数据的中位数.
【解析】显然根据题目中的三个条件要直接求出这九个数是不可能的,但如果把前4个数看作一个整体,后4个数也看作一个整体,可设前4个数的和为a,后4个数的和为b,中位数(即中间数)为x.
由题意可得a+x=20×5,b+x=41×5,
则a=100-x,b=205-x.
因为a+x+b=30×9,
所以100-x+x+205-x=270,x=35.
即中位数为35.
三、分类思想
例3 陈老师想对同学们的打字能力进行测试,他将全班同学分为4个小组.经统计,这4个小组平均每分钟打字的个数如下:100,80,x,100.已知这组数据的中位数与平均数相等,那么x的值为____.
【解析】要确定中位数,就要先把这4个数进行排序,而我们不知道x处于什么位置,因此要利用分类思想.
(1)当x≥100时,这组数据为80,100,100,x,中位数是100.
根据中位数与平均数相等,得80+100+x+100=100×4,解得x=120.

综上所述,x的值为120或80.
四、数形结合思想
例4 某射击小组有20人,教练根据他们某次射击的数据绘制成条形统计图,则这组数据的众数是____.
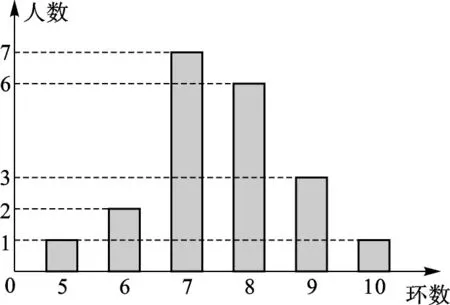
【解析】根据条形统计图可知,环数为5,6,7,8,9,10的人数依次为:1,2,7,6,3,1,其中环数7出现了7次,次数最多,即为这组数据的众数.
(作者单位:江苏省宿迁市泗洪县第一实验学校)

