轮胎胎压和车速对无悬架拖拉机横向乘坐振动特性的影响

薛金林，汪珍珍，李毅念，丁启朔，林相泽



轮胎胎压和车速对无悬架拖拉机横向乘坐振动特性的影响

薛金林，汪珍珍，李毅念，丁启朔，林相泽

（1. 南京农业大学工学院，南京210031；2. 江苏省智能化农业装备重点实验室，南京210031）

为研究轮胎胎压和行驶速度对驾驶员横向乘坐振动特性的影响，该文以两轮驱动式无悬架国产拖拉机为研究对象，建立无悬架拖拉机横向-垂向平面三自由度模型，通过仿真和试验相结合，分别获取不同轮胎胎压和行驶速度下拖拉机座椅处横向加速度功率谱密度、横向加速度均方值以及总加权加速度均方根值，并分析各自的影响规律。结果表明：拖拉机座椅处横向固有频率试验值与理论计算值的最大相对误差为4.67%，座椅处横向加速度均方根试验值随后轮胎胎压和速度的变化规律与仿真是一致的，且试验值比仿真值要小，其相对误差最大值为5.26%，误差均在可接受范围内，表明建立的理论和仿真模型是可行的；前轮胎压的变化对两轮驱动式拖拉机乘坐横向振动特性的影响不大；当轮胎胎压不变时，试验获取的拖拉机座椅处总加权加速度均方根值随行驶速度的增大而增大；当行驶速度不变时，总加权加速度均方根值随后轮胎压的增大而波浪式增大。该研究为拖拉机多维减振悬架系统的设计提供参考。

拖拉机；轮胎；胎压；行驶速度；振动特性

0 引 言

驾驶员长期在高强度低频全身振动的环境下工作，不仅会引起脊柱畸形、劳损扭伤、关节疼痛、胃下垂、神经衰弱等职业病变，还会促使噪声性耳聋、前列腺炎、痔疮、高血压等疾病的加剧[1-5]。因此拖拉机乘坐振动特性的研究一直是国内外学者和企业关注的重点[6-7]。

Langer等对悬挂打捆机的四轮驱动Vattra 8550型拖拉机进行了上下坡行驶时整车纵向振动动态响应特性测试与分析[8]。Zeinab等对ITM399型拖拉机在犁耕、旋耕、干草打捆和运输4种不同作业状况下的驾驶员乘坐舒适性进行了试验研究，分析了拖拉机驾驶员线振动方向（垂向、横向和纵向）的加速度功率谱密度，试验结果表明，除了拖拉机运输工况，其余3种工况下，通过座椅传递给驾驶员全身振动能量最大幅值都发生在低频5 Hz以下[9]。Kabir等基于ISO标准分别在4类路面上以不同的速度测试前后桥与驾驶室都无减振系统的DK470型拖拉机座椅处的振动特性[10]。Servadio等研究了2类轮胎和2种行驶速度对有驾驶室减振系统的中型拖拉机乘坐振动特性的影响，结果表明驾驶员的总加权加速度均方值均受轮胎类型和行驶速度的影响[11]。Cuong等分析了行驶速度、轮胎胎压和土壤含水率这三个因素对无悬架拖拉机前桥、后桥和机身振动特性的影响规律，研究结果表明，拖拉机前桥、后桥和机身振动加速度均方值随着速度和轮胎胎压的减小都明显减小，且更受后轮胎压的影响[12]。

迄今为止，国内外学者已经从轮胎、座椅、驾驶室、前后悬架等方面进行了减振研究，但关于拖拉机的横向乘坐振动特性较少，如Gomez-Gil等研究了座椅安装的离地高度对驾驶员横向振动特性的影响[13]。课题组前期已经对国产拖拉机振动系统的横向固有频率进行了研究，提出了振动系统的横向固有频率理论计算方法[14]。而本文在前期研究基础上基于轮胎胎压和行驶速度两个影响因素进一步研究驾驶员的横向乘坐舒适性。仍以典型的无悬架两轮驱动式国产CF700型拖拉机为试验对象，建立拖拉机横向-垂向（-）平面三自由度横向振动模型，用仿真和试验相结合的方法，分析轮胎胎压和行驶速度对两轮驱动式无悬架拖拉机横向乘坐振动特性的影响，以期为国产拖拉机多维减振悬架系统的设计提供参考，从而进一步地提高拖拉机驾驶员的乘坐舒适性。

1 乘坐横向振动微分方程的建立

目前国内拖拉机普遍没有悬架减振装置，轮胎是唯一的减振元件。本文选用两轮驱动式常发集团CF700型拖拉机作为研究对象。为研究方便和提高研究结果的可靠性，作如下假设：1）拖拉机采用刚性悬架结构，轮胎作为车辆与地面间唯一的弹性支撑元件，将其简化为线性弹簧—阻尼器元件[15-16]；2）拖拉机结构关于中心面左右对称[17]；3）拖拉机前进过程中前、后轮所受到的路面激励高度差忽略不计，而只考虑左、右轮所受到路面激励的不同；4）左、右轮所受路面激励引起的车辆侧倾角很小，且绕后轴中心侧倾；5）驾驶员座椅安装于后桥上方，前桥对横向振动的影响很小[13]。故不考虑前轮胎模型。因此，建立如图1所示的无悬架拖拉机横向-垂向（-）平面三自由度横向振动模型。

注：O为拖拉机质心；Os为拖拉机座椅与驾驶员一体的质心；O′为拖拉机后轮车轴中心；ms为拖拉机后轴载荷质量，kg；Jy为拖拉机绕纵向中心轴的转动惯量，kg·m2；θ为拖拉机侧倾振动角位移，rad；ky为后轮横向刚度系数，N·m-1；kz为后轮径向刚度系数，N·m-1；cy为后轮横向阻尼系数，N·s·m-1；cz为后轮径向阻尼系数，N·s·m-1；h为质心Os距后轴高度，m；b为后轮轮半距，m；zs为质心Os处垂向位移，m；ys为质心Os处横向位移，m；y0为拖拉机轮胎受路面激励产生的横向位移，m；hl为拖拉机左后轮受路面激励产生的垂向位移，m；hr为拖拉机右后轮受路面激励产生的垂向位移，m。

基于图1所示拖拉机-平面三自由度横向振动模型，得振动微分方程如式（1）～式（3）

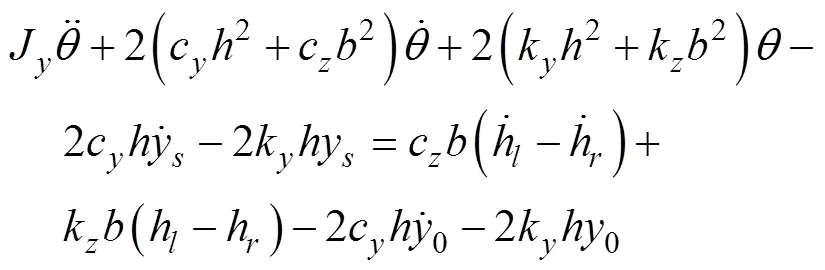
将式（3）改写成状态空间表达式

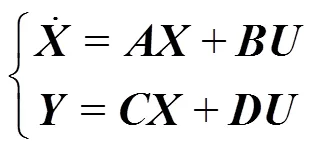
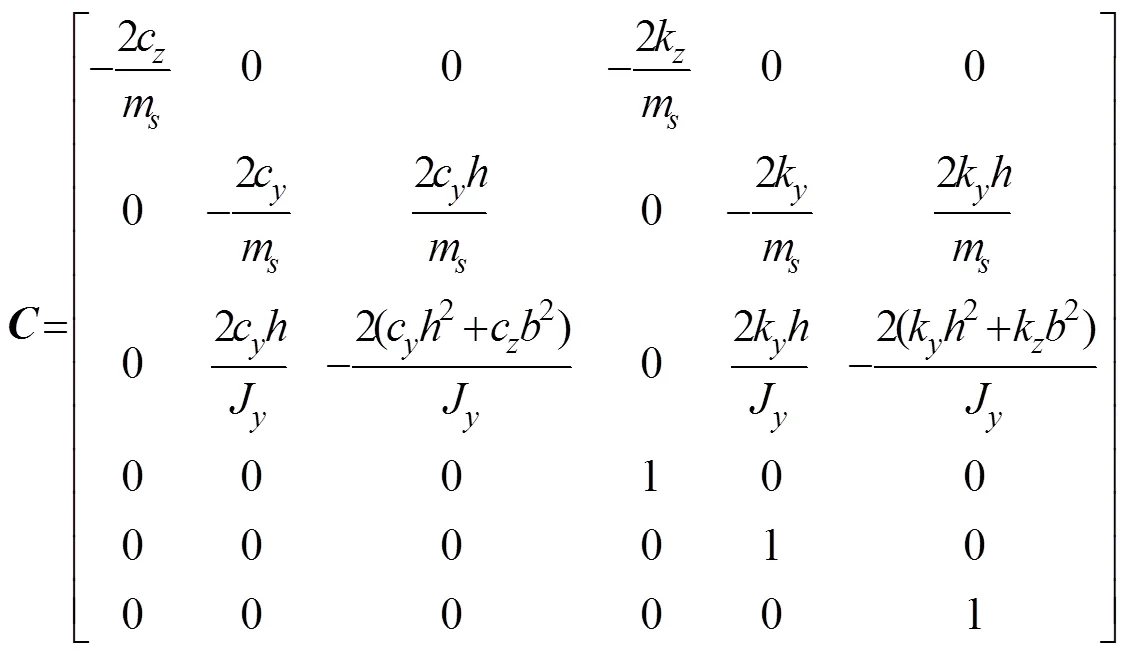
2 横向振动系统参数的获取

课题组前期已经对常发集团CF700型拖拉机进行了相关振动技术参数的获取[18-21]。本文所用到的有关参数见表1与前期研究文献[14]。

表1 CF700型拖拉机部分参数

3 仿真与试验方案设计

3.1 仿真方案

基于MATLAB/SIMULINK软件建立拖拉机座椅处振动系统三自由度仿真振动模型[22]，如图2所示。该仿真振动模型中的输入为作用在左、右后轮胎上的100 m长较平滑的试验跑道路面垂向激励和相对横向激励及其微分[23]；状态空间方程由式（4）表示，该式中矩阵各元素值可由CF700拖拉机振动系统相关参数及公式计算求得；输出矢量由拖拉机座椅处振动的垂向加速度、横向加速度、侧倾角加速度及相应的位移量组成。后轮胎压变化范围为60～180 kPa，胎压变化差值为30 kPa；行驶速度取值为3.5、6、9和12 km/h。然后进行不同轮胎胎压和不同车速对驾驶员座椅处横向振动加速度影响的仿真与分析。

注：simin1、simin2和simin3分别为作用在左、右后轮胎上的100 m长较平滑的试验跑道路面垂向激励和相对横向激励；du/dt 为一阶微分；zacc、yacc和citaacc分别为拖拉机座椅处振动的垂向加速度、横向加速度和侧倾角加速度；zdis、ydis和citadis分别为垂向位移、横向位移和侧倾角位移。

3.2 试验设备与方案

选择在江苏省农机试验鉴定站的双辙较平滑100 m国家标准跑道上[24]，对CF700拖拉机进行整车振动测试，改变轮胎胎压和行驶速度，从而获取驾驶员座椅处三个方向的振动加速度。由于上文中所建立的横向振动理论和仿真模型都未考虑前轮轮胎，因此在试验验证时将前轮胎胎压纳入考虑，以验证未考虑前轮轮胎而所建立的振动理论模型和仿真模型是否合适。

本试验中所需要的主要仪器设备有：1）比利时LMS公司生产的SCM05型SCADAS Mobile便捷式动态信号测量仪1台，可同时测量40个通道的信号，安装有LMS Test.Xpress软件的笔记本一台和网线一根；2）江苏联能电子科技有限公司生产的CA-YD-152A型压电式三向加速度传感器和一个装有三向加速度传感器的圆盘和若干个与仪器和传感器连接的导线；3）将直流电压12 V转换为交流电压220 V的逆变器一个；4）小型轮胎充气泵1台和气压表1只。

试验获取拖拉机的前、后轮胎压、车速和座椅处的加速度。利用充气泵和气压表对轮胎胎压进行调节和测量；车速的测量采用固定距离测速法；加速度的获取采用LMS振动测试分析仪。CF700型拖拉机前轮轮胎的推荐工作压力为210 kPa，其允许充气压力范围为120～240 kPa，后轮轮胎推荐工作压力为120 kPa，其允许充气压力范围为60～180 kPa。

方案步骤：1）拖拉机前轮胎压值设定为210 kPa，改变后轮胎压值，间隔30 kPa，拖拉机分别以3.5、6、9和12 km/h的速度行驶，且每种速度下重复试验3次；2）拖拉机后轮胎压值设定为120 kPa，改变前轮胎压值，间隔30 kPa。同样以四种速度行驶，且每种速度下重复试验3次。图3为拖拉机乘坐振动测试仪器和现场，安装有三向加速度传感器的圆盘安装于座椅椅面上，并位于驾驶员臀部之下。

1. 驾驶员 2. CF700拖拉机 3. 100 m较平滑GB跑道 4. 轮胎充气泵和气压表 5. 安装有三向加速度传感器的圆盘6. LMS测试系统

4 仿真与试验结果分析

为了提高数据分析的准确性，只选取所测得的离散数据中间部分，并进行五点三次平滑处理[25]，将处理后的数据进行傅里叶变换和相关的计算，得到拖拉机振动系统座椅处的横向加速度功率谱密度和横向加速度均方值以及座椅椅面处总加权加速度均方值。

4.1 座椅处横向加速度功率谱密度

将试验获取的横向加速度时域数据进行快速傅里叶变换得其加速度功率谱密度，功率谱密度峰值所对应的频率即为横向振动固有频率[26-28]。

4.1.1 轮胎胎压的影响分析

拖拉机行驶速度为9 km/h，先后改变前、后轮胎胎压，分析前、后轮胎压对拖拉机乘坐横向加速度功率谱密度的影响。图4为后轮胎压120 kPa时改变前轮胎压值所获取的横向加速度频域图。图5为前轮胎压210 kPa时改变后轮胎压值所获取的横向加速度频域图。

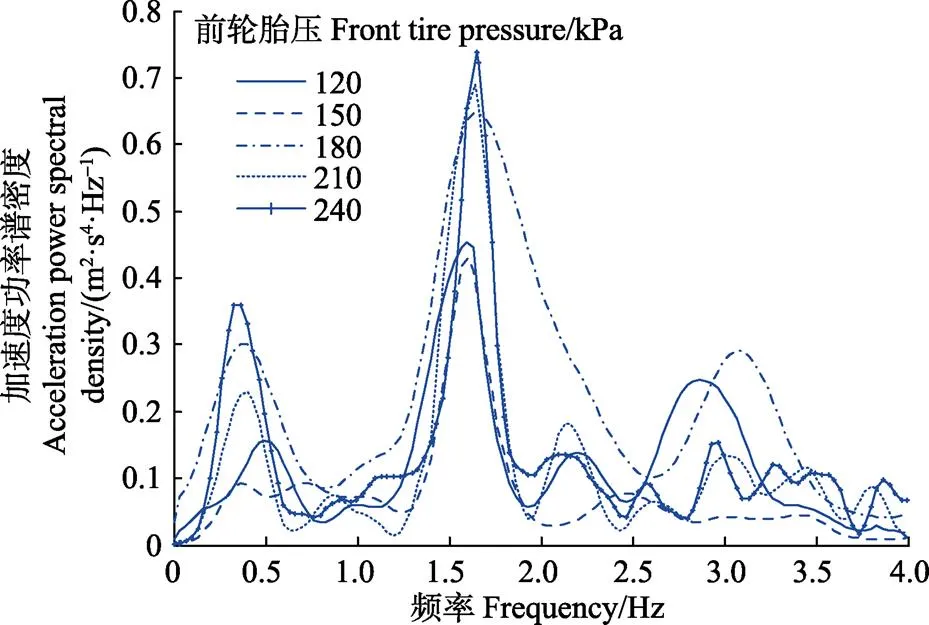
注：后轮胎压为120 kPa，行驶速度为9 km·h-1。

注：前轮胎压为210 kPa，行驶速度为9 km·h-1。

从图4中可以发现，无论前轮胎压值如何变化，拖拉机座椅处的横向固有频率都处在人体横向敏感频率1~2 Hz范围内，且拖拉机座椅处横向固有频率变化幅度不大。当前轮胎压为180 kPa时，座椅处横向振动强度明显增大，但之后横向振动强度变化不大。

从图5中可以看出，无论后轮胎压如何变化，拖拉机座椅处横向固有频率亦处于人体水平敏感频率1～2 Hz范围内，但随着后轮胎压值的增大，拖拉机座椅处横向固有频率逐渐增大。除了后轮胎压为150 kPa时座椅处横向振动强度有所减小之外，横向振动强度总体上呈现增大趋势，表明随着后轮胎压的增大，后轮胎对于横向方向的减振效果越来越小，驾驶员感受到的横向振动将会越来越明显。通过与图4对比，后轮胎压对座椅处横向固有频率与横向振动强度的影响要比前轮胎压的影响大得多。

表2为行驶速度为9 km/h、前轮胎压210 kPa时，改变后轮胎压所获取的座椅处横向固有频率理论值与试验值比较结果。在60、90、120、150、180 kPa后轮胎压下拖拉机座椅处横向固有频率理论计算值与试验值的相对误差分别为4.67%、0.31%、0.43%、0.91%和0.06%，最大相对误差为4.67%，表明本文建立的无悬架拖拉机－平面横向振动理论和仿真模型是可行的。当后轮胎压为60 kPa时相对误差最大，这是由于后轮胎压越小时，试验时滚动轮胎的非线性特性将越明显，而建立的理论和仿真模型中的轮胎模型选取的是线性弹簧-阻尼模型；当后轮胎压为180 kPa时相对误差最小，此时试验所得横向振动强度最大，这是由于随着后轮胎压的逐渐增大，轮胎的横向减振效果越来越小的缘故。

表2 座椅处横向固有频率仿真与试验结果比较

4.1.2 车速的影响分析

拖拉机前、后轮胎压分别为210和120 kPa，车速分别为3.5、6、9和12 km/h时，试验所获取的座椅处横向加速度功率谱密度如图6所示。可知，座椅处横向固有频率随着速度增大而缓慢增大，但座椅处横向振动强度随速度增大而快速增大。当速度为12 km/h时，座椅处横向加速度功率谱第二波峰猛然增大，表明此时横向振动和侧倾振动有明显的耦合现象，这样座椅处横向振动传递给驾驶员的强度会更为强烈。

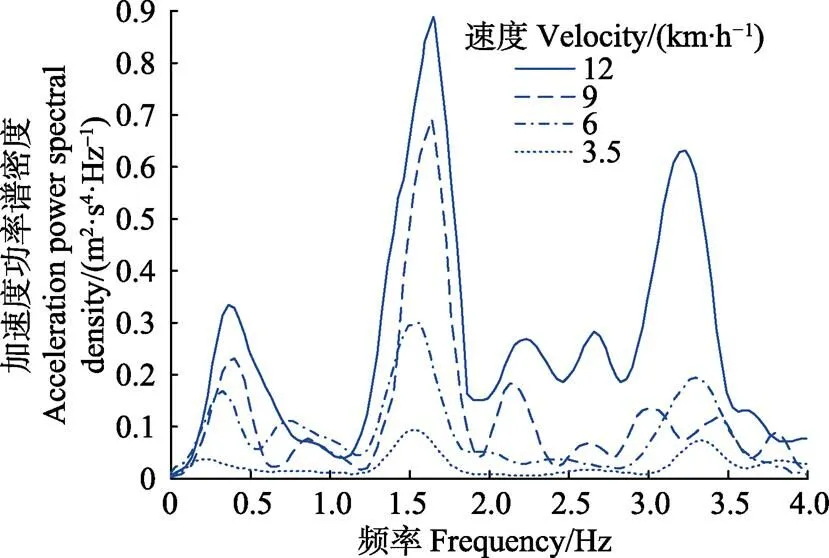
注：前轮胎压为210 kPa，后轮胎压为120 kPa。

4.2 座椅处横向加速度均方值

4.2.1 前轮胎压和车速对加速度均方值的影响

拖拉机后轮胎压设定推荐胎压值120 kPa，分别以3.5、6、9和12 km/h的速度行驶，改变前轮胎压值所获取的拖拉机座椅处横向加速度均方根试验值如图7所示。当拖拉机行驶速度不超过6 km/h时，试验所获取的横向加速度均方根值变化不大，可以说是在某一值上下波动，此时前轮胎压的变化对其影响不大；当拖拉机行驶速度不小于9 km/h时，在前轮胎压为180 kPa时，所获取的座椅处横向加速度试验值突然剧增，且随着行驶速度的增大，这种骤增幅度会明显减小，出现该现象是由于此时轮胎某阶固有频率处于驾驶员座椅处固有频率附近，从而导致振动加速度均方值波动很大。若去除前轮胎压为180 kPa的异常情况，则座椅处横向加速度试验值也几乎保持不变。

图7 前轮胎压和速度对座椅处横向加速度均方根值的影响

拖拉机行驶速度为3.5和6 km/h时，不同前轮胎压时座椅处横向加速度均方值分别在0.885和0.98 m/s2上下波动。在前轮胎压为180 kPa时，当行驶速度为9 km/h，横向加速度均方值陡然增大；当行驶速度为12 km/h，亦出现类似现象，引起此现象的原因是当前轮胎压为180 kPa时，随着行驶速度的增大，轮胎某阶固有频率接近拖拉机座椅处的固有频率引起共振而使得横向加速值突然增大。因此，除了180 kPa之外，前轮胎压对拖拉机座椅处横向加速度均方值的影响不大。

不论前轮胎压如何变化，对两轮驱动式拖拉机乘坐横向振动特性影响都不大，这进一步验证了未考虑前轮轮胎而建立的振动理论模型和仿真模型的可行性。

4.2.2 后轮胎压和车速对加速度均方值的影响

拖拉机前轮胎压设定为210 kPa，改变后轮胎压值和行驶速度所获取的横向加速度均方根试验值与仿真值的比较如表3所示。可以看出，试验和仿真所得到的拖拉机座椅处横向振动加速度均方根值的变化规律是一致的，即在同一轮胎胎压下，横向加速度均方根值随行驶速度的增大而增大，仿真值变化趋势比较平稳，而试验值变化起伏较大，这主要是由于实际整车试验过程中环境因素变化引起。

仿真结果与试验结果相对误差最大值为5.26%，最小值为0.61%，较好地反映了拖拉机座椅处横向加速度均方值变化规律。当行驶速度不小于6 km/h时，拖拉机座椅处横向加速度的试验值和仿真值均随后轮胎压的增大而增大；当行驶速度为3.5 km/h时，拖拉机座椅处横向加速度试验值在0.911 2 m/s2之间波动，而仿真值则随后轮胎压的增大缓慢增大，这是因为在实车试验中，拖拉机低速行驶时的轮胎非线性特性更加明显。当拖拉机行驶速度为12 km/h时，座椅处横向加速度试验值与仿真值的相对误差要比其他速度下普遍大，这是因为当行驶速度大于10 km/h时，滚动轮胎刚度将逐渐趋于稳定，而仿真中轮胎是线性弹簧—阻尼模型。

表3 改变后轮胎压和车速拖拉机座椅横向加速度试验与仿真结果对比

利用MATLAB对试验值进行最小二乘法拟合[29]，改变后轮胎压和车速获取的横向加速度均方根试验值拟合曲线如图8所示。可以看出，随着后轮胎压的增大，不同速度下，拖拉机座椅处横向加速度均方根值都呈现增大趋势，且拖拉机前进速度越大，横向加速度增加幅度也越大。4种速度下座椅处横向加速度均方根值随后轮胎压变化的拟合曲线方程分别为

式中a为拖拉机座椅处横向加速度均方根值，m/s2；为后轮胎压，kPa；为行驶速度，km/h。

4个回归方程曲线的拟合度2都很高，分别为0.984、0.968、0.964和0.978，其中拟合度2的最大值为0.984，说明在不同行驶速度下，拖拉机座椅处横向加速度均方根值与后轮胎压的关系可以用对数函数表示。

图8 后轮胎压和车速对横向加速度的拟合曲线

4.3 座椅处总加权加速度均方值

对于人体振动的评价参数除了单轴向加速度均方根值之外，还有总加权加速度均方根值，即3个线振动轴向加速度均方根值的矢量和[30]。拖拉机前轮胎压设定为推荐胎压值210 kPa，改变后轮胎压值和行驶速度，试验获取的总加权加速度均方根值如图9所示。当拖拉机前轮胎压不变时，座椅处总加权加速度均方根值随行驶速度的增大而增大；当行驶速度不变时，总加权加速度随后轮胎压的增大而有波动，但总体上呈现出增大趋势。当拖拉机行驶速度为12 km/h，后轮胎压变化为150 kPa时，试验获取的总加权加速度均方根值最大为3.685 m/s2，远远超过了国际标准给出的最大界限值[31]，而其最小值1.398 m/s2出现在行驶速度为3.5 km/h，后轮胎压为120 kPa处，此时人的主观感觉程度亦处于很不舒服状态。

表4为CF700型拖拉机前、后轮胎压均为推荐工作压力时，随着行驶速度的增大，该拖拉机驾驶员的主观感觉与座椅处横向加速度均方值和其等效均值一一对应关系。将表5中的结果与国际推荐的评判标准表[32]4进行对照可以得出，该CF700型拖拉机作业时会严重危害人的身心健康，就其单轴横向方向的振动，即使行驶速度为3.5 km/h，其产生的横向振动强度也使人的主观感觉处于相当不舒适和不舒适之间；而当拖拉机以12 km/h的速度行驶时，人的主观感觉程度则为很不舒适。因此，需要安装减振悬架系统以降低传递给驾驶员的振动。

图9 拖拉机座椅处总加权加速度均方根值与后轮胎压关系曲线

表4 等效均值和加速度均方根值与人的主观感觉之间的关系

表5 试验获取横向振动方向的等效均值和加速度均方根值与人的主观感觉之间的关系

5 结 论

本文用仿真和试验相结合的方法，分析了前、后轮胎胎压和行驶速度对两轮驱动式拖拉机乘坐横向振动特性的影响，得到如下结论：

1）随着前、后轮胎压值的变化，拖拉机座椅处横向固有频率都处在人体横向敏感频率1～2 Hz范围内；前轮胎压的变化对横向固有频率影响不大，而随着后轮胎压值的增大，横向固有频率逐渐增大。横向固有频率试验值与理论计算值的最大相对误差出现在后轮胎压为60 kPa时，其值为4.67%，若剔除后轮胎压为60 kPa时的试验值，则最大相对误差为0.91%，表明建立的理论和仿真模型用来估算拖拉机座椅处横向固有频率是可行的。

2）同一速度下，前轮胎压的变化对座椅处横向加速度均方根值影响不大，而增大后轮胎压，横向加速度均方根值则逐渐增大。这验证了未考虑前轮轮胎而建立的振动理论模型和仿真模型的可行性。

3）拖拉机行驶速度的变化，对座椅处横向固有频率影响较小，但随着速度的增大，座椅处横向振动强度和横向加速度均方根值都逐渐增大。

4）拖拉机座椅处总加权加速度均方根值随行驶速度的增大而增大，随后轮胎压的增大呈现增大趋势。另外，拖拉机即使以最低速度行驶，驾驶员的主观感觉仍为不舒适。因此，需要安装悬架系统以减小传递给驾驶员的横向振动。

研究结论可为拖拉机多维减振系统的设计提供了重要参考。

[1] 刘娟. 全身振动对人体身心健康影响的研究进展[C]//白云. 2016年全国声学设计与演艺建筑工程学术会议论文集，2016：162－165. Liu Juan. The progress of the research on whole body vibration impacts on the physical and mental health of human beings[C]//Bai Yun, Proceedings of 2016 Academic Conference on acoustical design and Performing Arts in China, 2016: 162－165. (in Chinese with English abstract)

[2] Cutini M, Costa C, Bisaglia C. Development of a simplified method for evaluating agricultural tractor’s operator whole body vibration[J]. Journal of Terramechanics, 2016, 63: 23－32.

[3] Park M S, Fukuda T, Kim T G, et al. Health risk evaluation of whole-body vibration by ISO 2631-5 and ISO 2631-1 for operators of agricultural tractors and recreational vehicles[J]. Industrial Health, 2013, 51(3): 364－370.

[4] 赵健业，杨宜谦. 人体承受全身振动响应研究综述[J]. 土木建筑与环境工程，2016，38(2)：44－53. Zhao Jianye, Yang Yiqian. Review of human body response to whole-body vibration[J]. Journal of Civil, Architectural and Environmental Engineering, 2016, 38(2): 44－53. (in Chinese with English abstract)

[5] Morioka M，Griffin M J. Magnitude dependence of equivalent comfort contours for fore-and-aft, lateral, and vertical vibration at the foot for seated persons[J]. Journal of Sound and Vibration, 2010, 329(14): 2939－2952.

[6] Subashi G，Nawayseh N，Matsumoto Y，et al. Nonlinear subjective and dynamic responses of seated subjects exposed to horizontal whole-body vibration[J]. Journal of Sound and Vibration, 2009, 321(1/2): 416－434.

[7] 王凯. 基于LabVIEW的农业轮式拖拉机驾驶员全身振动测评系统的研究[D]. 呼和浩特：内蒙古农业大学，2013. Wang Kai. LabVIEW Based Research on Whole Body Vibration Measurement and Evaluation System Specific to Agricultural Wheeled Tractor Operators[D]. Hohhot: Inner Mongolia Agricultural University, 2013. (in Chinese with English abstract)

[8] Langer T H, Ebbesen M K, Kordestani A. Experimental analysis of occupational whole-body vibration exposure of agricultural tractor with large square baler[J]. International Journal of Industrial Ergonomics, 2015, 47: 79－83.

[9] Zeinab K, Hojjat A, Seyed Saeid M. Whole body vibration analysis of tractor operators using power spectral density[J]. Journal of Mechanical Engineering and Technology, 2013, 1(1): 6－12.

[10] Kabir M S N, Chung S, Kim Y. Measurement and evaluation of whole body vibration of agricultural tractor operator[J]. International Journal of Agricultural & Biological Engineering, 2017, 10(1): 248－255.

[11] Servadio P, Belfiore N P. Influence of tyres characteristics and travelling speed on ride vibrations of a modern medium powered tractor part 1: Analysis of the driving seat vibration [J]. Agricultural Engineering International: The CIGR e- journal, 2013, 15(4): 119－131.

[12] Cuong D M, Zhu S, Zhu Y. Effects of tyre inflation pressure and forward speed on vibration of an unsuspended tractor[J]. Journal of Terramechanics, 2013, 50(3): 185－198.

[13] Gomez-Gil J, Gomez-Gil J F, Martin-de-Leon R. The influence of tractor-seat height above the ground on lateral vibration[J]. Sensors, 2014, 14: 19713－19730.

[14] 薛金林，汪珍珍，伊力达尔·伊力亚斯，等. 轮式拖拉机振动系统横向固有频率研究[J]. 农业工程学报，2016，32(19)：51－56. Xue Jinlin, Wang Zhenzhen, Yilidaer Yiyasi, et al. Lateral natural frequency modeling and verification for vibration systems of wheeled tractors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(19): 51－56. (in Chinese with English abstract)

[15] 刘大维，刘伟，陈焕明，等. 基于多体模型的重型车辆对路面动载特性[J]. 农业机械学报，2009，40(11)：7－12. Liu Dawei, Liu Wei, Chen Huanming, et al. Dynamic load characteristics of heavy vehicle based on multi-body dynamic model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(11): 7－12. (in Chinese with English abstract)

[16] 徐刚. 拖拉机+悬挂农具系统振动特性及悬挂农具吸振技术研究[D]. 南京：南京农业大学，2015. Xu Gang. Research on Vibration Characteristic of Tractor- implement System and Implement Absorption Technology[D]. Nanjing: Nanjing Agricultural University, 2015. (in Chinese with English abstract)

[17] 伊利达尔•伊力亚斯，朱思洪，徐刚，等.拖拉机前桥悬架参数匹配及其对振动特性的影响[J].农业工程学报，2015, 31（10）：29－36.

Yilidaer×Yiliyasi, Zhu Sihong, Xu Gang, et al. Front axle suspension parameters match and its impact on vibration characteristics of tractor[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(10): 29－36.(in Chinese with English abstract)

[18] 江苏常发集团. CF700轮式拖拉机技术参数与使用说明[Z].

[19] 聂信天，史立新，顾浩，等. 基于质量反应法的拖拉机质心高度测量方法[J]. 农业工程学报，2011，27(13)：336－339. Nie Xintian, Shi Lixin, Gu Hao, et al. Determination method of the height of tractors gravity center based on mass- response[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2011, 27(13): 336－339. (in Chinese with English abstract)

[20] 聂信天，史庆春，朱思洪，等. 拖拉机转动惯量测量及误差分析[J]. 机械科学与技术，2012，31(8): 1325－1328. Nie Xintian, Shi Qingchun, Zhu Sihong, et al. Method of measuring the moment of inertia of tractors and the error analysis[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(8): 1325－1328. (in Chinese with English abstract)

[21] 聂信天，史立新，顾浩，等. 农用轮胎径向刚度和阻尼系数试验研究[J]. 南京农业大学学报，2011，34(5)：139－143. Nie Xintian, Shi Lixin, Gu Hao, et al. Research on the radial stiffness and damping of tractor coefficient tires through test[J]. Journal of Nanjing Agricultural University, 2011, 34(5): 139－143. (in Chinese with English abstract)

[22] 张春红. 基于MATLAB 的汽车振动系统仿真[J]. 机械工程与自动化，2008，147(2)：83－84. Zhang Chunhong. Study on automobile vibration system based on MATLAB[J]. Mechanical Engineering & Automation, 2008, 147(2): 83－84. (in Chinese with English abstract)

[23] 陈杰平，陈无畏，祝辉, 等. 基于Matlab-Simulink 的随机路面建模与不平度仿真[J]. 农业机械学报，2010，41(3)：11－15. Chen Jieping, Chen Wuwei, Zhu Hui, et al. Modeling and simulation on stochastic road surface irregularity based on Matlab/Simulink[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 11－15. (in Chinese with English abstract)

[24] GB/T 10910－2004，农业轮式拖拉机和田间作业机械驾驶员全身振动的测量[S].

[25] 朱思洪，徐刚，袁加奇，等. 农具质量对拖拉机悬挂农具系统振动特性的影响[J]. 农业工程学报，2014，30(24)：30－37.

Zhu Sihong, Xu Gang, Yuan Jiaqi, et al. Influence of implement’s mass on vibration characteristics of tractor- implement system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(24): 30－37. (in Chinese with English abstract)

[26] Dave C，喻凡. 车辆动力学及其控制[M]. 北京：人民交通出版社，2004.

[27] 叶元瑜. 拖拉机乘坐振动理论分析[J]. 农业机械学报，1982，13(1)：19－31. Ye Yuanyu. Theoretical analysis of tractor ride vibration[J]. Transactions of the Chinese Society for Agricultural Machinery, 1982, 13(1): 19－31. (in Chinese with English abstract)

[28] 黄俊明，周孔亢，徐兴，等. 空气悬架固有频率试验研究及理论分析[J]. 机械工程学报，2011，47(14): 114－120.

Huang Junming, Zhou Kongkang, Xu Xing, et al. Theoretical analysis and test research of eigen-frequency of air suspension[J]. Journal of Mechanical Engineering, 2011, 47(14): 114－120. (in Chinese with English abstract)

[29] 张德丰. MATLAB数值分析：第2版[M]. 北京：机械工业出版社，2012.

[30] 唐传茵，张天侠，李华，等. 汽车振动舒适性评价研究[J]. 振动与冲击，2008，27(9): 158－161. Tang Chuanyin, Zhang Tianxia, Li Hua, et al. Evaluation of ride comfort of a vehicle[J]. Journal of Vibration and Shock, 2008, 27(9): 158－161. (in Chinese with English abstract)

[31] ISO2631《人体承受全身振动的评价指南》[S].

[32] ISO2631-1：1997(E)《人体承受全身振动评价第一部分：一般要求》[S].

薛金林，汪珍珍，李毅念，丁启朔，林相泽. 轮胎胎压和车速对无悬架拖拉机横向乘坐振动特性的影响[J]. 农业工程学报，2017，33(19)：94－101. doi：10.11975/j.issn.1002-6819.2017.19.012 http://www.tcsae.org

Xue Jinlin, Wang Zhenzhen, Li Yinian, Ding Qishuo, Lin Xiangze. Influence of tire pressure and forward speed on lateral ride vibration characteristics for unsuspended tractor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 94－101. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.19.012 http://www.tcsae.org

Influence of tire pressure and forward speed on lateral ride vibration characteristics for unsuspended tractor

Xue Jinlin, Wang Zhenzhen, Li Yinian, Ding Qishuo, Lin Xiangze

(1.210031,;2.210031,)

The operators of agricultural tractors experience whole-body vibration when they drive tractors, and the main influence factors to ride vibrations of the operators are terrain roughness, tractor speed, tire type, pressure, and so on. In this paper, the effects of tire pressure and forward speed on lateral ride vibration characteristics of a two-wheel drive unsuspended tractor was studied by means of a theoretical simulation and experimental analysis. A CF700 tractor without suspensions from Changfa Group was chosen as the research object, and a new theoretical vibration model was constructed for the two-wheel drive unsuspended tractor with 3 degrees of freedom including the lateral and roll and vertical directions of ride vibration in Y-Z plane. Simulation and real tractor experiments were conducted respectively to obtain the natural frequencies of lateral vibration, root mean square (RMS) of lateral acceleration and RMS of total weighted acceleration on the tractor seat under different tire pressures and forward speeds of the tractor, and thus to analyze their respective influence laws. Simulation model was built up on the basis of the constructed state space equation of tractor seat vibration system by using MATLAB/Simulink software, and then simulation was performed when rear tire pressures varied from 60 to 180 kPa with the increment of 30 kPa and 4 forward speeds of 3.5, 6, 9 and 12 km/h were chosen. Meanwhile, driving experiments of the CF700 tractor were carried out on an ISO-5008 standard trial track with 100 m length under the same conditions of rear tire pressures and forward speeds, while front tire pressures were considered from 120 to 240 kPa with the increment of 30 kPa. Firstly, the tests were repeated 3 times at the different forward speeds, when the front tire pressure was fixed to 210 kPa, while the rear tire pressure was changed from 60 to 180 kPa with the increment of 30 kPa. Then, the tests were repeated 3 times at the different forward speeds, when the rear tire pressure was fixed to 120 kPa, while the front tire pressure was changed from 120 to 240 kPa with the increment of 30 kPa. The experimental values were obtained mainly with the LMS test system and the on-board strain-gage-based transducers and triaxial accelerometers. The discrete time series of the measured data were resolved and reconstructed by wavelet and Fourier analysis. Results were obtained in light of the measurement of both the RMS of acceleration and the frequency, for any axis on the tractor operator seat. The results showed that the maximum relative error between the test value and the calculated value of lateral natural frequency was 4.67%, and the error was within the acceptable range, indicating that it is feasible for the established theoretical and simulation model to estimate the lateral ride natural frequency. The change of the tire pressure and velocity in the experiment was consistent with that in the simulation, and the test value was smaller than the simulation value; the maximum value of the relative error was 5.26%, and the minimum relative error was 0.61%. The change of the front tire pressure had little effect on the lateral vibration characteristics of the two-wheel drive tractor, which could verify that it is appropriate to establish the theoretical model and simulation model without considering the front tire. When the tire pressure is constant, the RMS value of the total weighted acceleration on the tractor seat is increased with the increase of the forward speed. When the forward speed is constant, the RMS value of total weighted acceleration is increased with a wave pattern with the increase of the rear tire pressure. This study provides an important reference for the design of multi-dimension vibration reduction suspension system for an unsuspended agricultural tractor.

tractors; tires; tire pressure; forward speed;vibration characteristics

10.11975/j.issn.1002-6819.2017.19.0012

S219.1

A

1002-6819(2017)-19-0094-08

2017-05-02

2017-09-14

国家自然科学基金资助项目（51275249）；江苏省自然科学基金（BK20151436）

薛金林，江苏涟水人，教授，主要从事农业车辆测控技术和智能化研究。南京 南京农业大学工学院，210031。Email：xuejinlin@njau.edu.cn