筒装料管道水力输送动边界环状缝隙流水力特性数值模拟
张春晋,孙西欢,2※,李永业,张学琴
筒装料管道水力输送动边界环状缝隙流水力特性数值模拟
张春晋1,孙西欢1,2※,李永业1,张学琴3
(1. 太原理工大学水利科学与工程学院,太原 030024;2. 晋中学院,晋中 030600;3. 章丘黄河河务局,济南 250200)
针对农产品长距离输送中存在的运输效率低和输送成本高等问题,提出了一种具有应用前景的农业机械运输方式—筒装料管道水力输送技术。该文基于Fluent软件,采用RNG-湍流模型、6DoF耦合模型以及PISO算法对动边界环状缝隙流进行数值模拟,分析不同环状缝隙宽度对动边界环状缝隙流场水力特性的影响。同时,对不同环状缝隙宽度条件下管道车在平直管道的运移进行模型试验,并将试验结果与模拟结果进行对比。结果表明:模拟结果和试验结果基本一致,最大相对误差不超过5.3%;动边界环状缝隙流中管道静边界区域压强呈现出进口区域压强降低,中间区域压强升高以及出口区域压强再次急剧降低的变化趋势;动边界环状缝隙流的水力特性不仅受到管道车动边界结构参数的影响,而且还受到管道车动边界上、下游管道内部流场的影响。该研究不仅完善了动边界环状缝隙流的相关理论,而且为进一步探究筒装料管道水力输送中动边界环状缝隙流水力特性提供了一种切实可行的研究手段。
CFD; 压强;流速;筒装料管道水力输送;环状缝隙流;水力特性;管道车
0 引 言
目前,中国农产品在长距离运输过程中存在着运输效率低与输送成本高等问题。针对上述弊端,本文提出了一种适用于长距离运输农产品的新型农业机械运输方式—筒装料管道水力输送技术。筒装料管道水力输送技术的原理是将农产品盛装并密封在圆柱状的管道车内部,并借助流体的推力实现管道车在有压管道内进行长距离运输[1]。该技术凭借其输送效率高、环境污染小以及运行稳定等优势逐渐发展成为了现代农业中最具有发展潜力的新型交通运输方式[2]。动边界环状缝隙流的水力特性是筒装料管道水力输送的一个重要研究方向,该项研究一方面可以完善动边界环状缝隙流的相关理论,另一方面也促进了管道车的动力学机理特性的研究。为此,国内外许多学者对筒装料管道水力输送的动边界环状缝隙流展开了大量的研究。
目前,对于筒装料管道水力输送动边界环状缝隙流主要采取了理论分析与模型试验相结合的研究思路。理论分析方面:Kroonenberg[3]建立了动边界环状缝隙流的数学模型,研究了动边界环状缝隙流的平均流速、动边界运移速度以及环状缝隙流压降三者之间的关系。Sud等[4]采用紊流关系与Von Karman相似性假设,分析了动边界环状缝隙区域内部充分发展的紊流模型。Azouz等[5]提出了一种用于求解动边界环状缝隙区域内部牛顿流体、非牛顿流体以及减阻流体等水力特性的单层涡流黏度模型。Khalil等[6]采用3种紊流模型分析了二维求解模型条件下动边界环状缝隙流沿程压降以及环形缝隙流断面轴向流速的分布规律。Polderman等[7-8]结合牛顿内摩擦定理,得出了动边界环状缝隙内部润滑流体的运动微分方程。Tomita等[9]提出了3种不连续动边界环状缝隙区域的绕流模型,并且采用特征线法求解了动边界环状缝隙流的水力特性。Ulusarslan等[10]采用量纲分析法预测了球状载体列车近壁面区域环状缝隙流的流体雷诺数与壁面摩擦阻力之间的变化关系。李永业等[11]假设环状缝隙流动工况为恒定流,并且提出了动边界环状缝隙区域内沿管道直径方向的轴向流速分布计算公式。许贤良等[12]结合黏性流体力学N-S方程,分析了同心环状缝隙区域的压降与流量之间的方程。上述理论分析中所建立的动边界环状缝隙流数学模型均忽略了动边界的运移阻力以及动边界上、下游端部对环状缝隙流水力特性的影响。模型试验方面:Yanaida[13]结合圆柱状和球状结构的载体,对比分析了在同心与非同心的动边界环状缝隙区域内部层流和紊流的流动特性。张雪兰等[14-15]探讨了3个典型的动边界环状缝隙断面的压强与流速的分布特性。井元昊等[16]比较了不同管道雷诺数条件下动边界环状缝隙断面的3维流速分布规律,为进一步选择最佳的管道输送雷诺数提供了重要的理论基础。孙蕾等[17]研究了管道车车中断面位置处的环状缝隙流场的径向流速与压强的分布规律。杨小妮等[18]结合封闭容器水力输送技术和螺旋流水力输送技术的相关思想,探究了动边界起旋器在运移过程中管道流场的水力特性。张琪琦等[19]采用模型试验的方法,对不同流量及环隙比条件下绕流圆柱体所形成的环隙流场进行了系统研究。模型试验虽然考虑了动边界上、下游端部对环状缝隙流水力特性的影响,但是测量中受到流场流动复杂、环状缝隙狭窄以及试验仪器落后等诸多因素的限制,使得试验结果不能全面反映动边界环状缝隙流场的水力特性。
数值模拟具有计算成本低与运算效率高等诸多优势,随着计算机性能的提高以及计算流体力学软件(computational fluid dynamics,CFD)研发技术的日益成熟,数值模拟已广泛用于求解多种复杂的水力学问题[20]。
本文的研究目的是采用Fluent 12.0软件对不同环状缝隙宽度条件下筒装料管道水力输送技术中动边界环状缝隙流的水力特性进行了数值模拟,既完善了动边界环状缝隙流的相关理论,又为进一步研究筒装料管道水力力输送的动边界环状缝隙流水力特性提供了一种切实可行的研究手段。
1 材料与方法
1.1 试验平台与管道车结构
为了更好地验证Fluent数值模拟结果的可靠性,本文对不同环状缝隙宽度条件下筒装料管道水力输送的动边界环状缝隙流水力特性进行了试验研究。本试验平台位于太原理工大学的水流试验大厅,试验平台是由动力装置、调节装置、输送装置以及投放与回收装置4个部分所组成[17],试验平台布置如图1所示。动力装置包括离心泵与水箱,其中水箱内部采用密度为1.05 g/cm3,且熔点为240℃的Polystyrene材质的示踪粒子。调节装置是由涡流流量计、调节阀以及管道车制动装置3部分所组成。输送装置为有机玻璃圆形管道,管道全长为28.62 m,管道内径为100 mm,管道壁厚为5 mm,而且不同管段之间采用圆形有机玻璃法兰密封连接。在有机玻璃管道内距管道车制动装置7.2 m的位置处布置了水槽,主要是用来防止激光在管道流场内部发生折射。投放与回收装置为管道车投放口、PVC稳流板以及塑料集车箱3个部分[14]。试验过程中,先通过离心泵将水流从水箱抽至钢管段,再通过涡流流量计与调节阀对管道流量进行调节,随后将水流注入有机玻璃管道。待管道内水流流动稳定,再将管道车通过投放口注入到试验输送管道系统,管道车在流体的作用下沿管道长距离运输,当到达试验测试断面设定位置时,对流场的水力特性进行测量,并将数据传输至计算机。运移结束后,管道车将到达塑料集车箱离开试验管道系统,此时管道内的流体将再次流回水箱。上述过程将形成一个闭合的循环系统[21]。
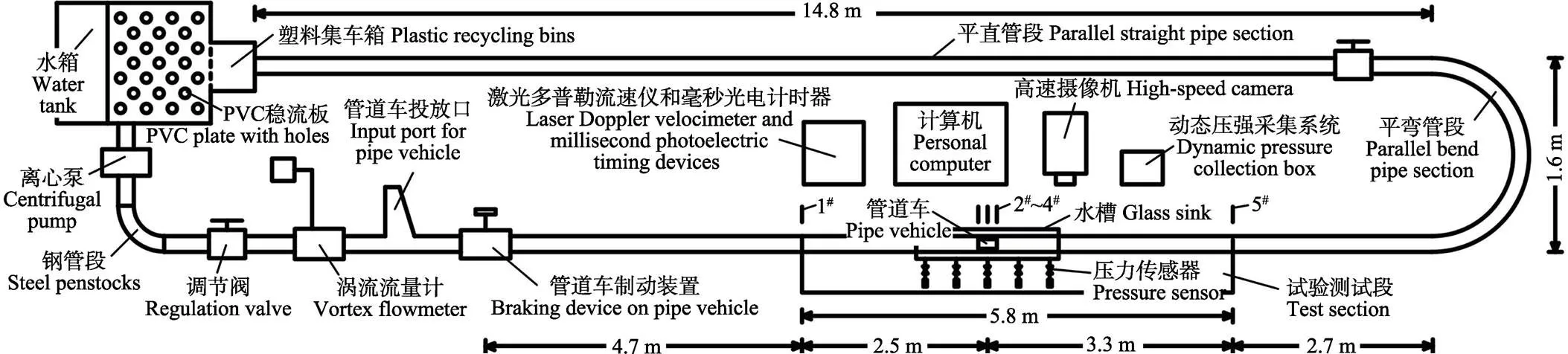
注:1#表示试验测试段进口断面,2#~4#表示3个试验测试断面,5#表示试验测试段出口断面。
管道车结构由料筒、支撑体及万向滚珠3部分所组成[2]。料筒为密闭的空心圆柱体结构。支撑体呈120°角等间隔呈放射状安装在管道车料筒的前后端面位置,该结构可以使管道车在管道内保持同心运动,从而提高管道车在管道内运移的稳定性。万向滚珠安装在靠近管道壁面处的支撑体的末端位置,可以有效地减小管道车与输送管道之间的摩擦阻力,在一定程度上起到了节能的目的[11]。
1.2 试验测试系统与数据分析
采用美国TSI公司的多普勒激光流速仪(laser doppler velocimeter,LDV,)和江苏扬泰光电公司的毫秒光电计时器(millisecond photoelectric timing device,PTD)协同测定动边界环状缝隙流的3维流速分布。采用苏州轩胜仪表公司的压力传感器与成都泰斯特电子公司的动态压强采集系统测量了动边界环状缝隙流管道壁面的沿程压强分布。日本活图隆公司的高速摄像机测量管道车在试验测试段任意位置的瞬时运动速度。各试验测量装置如图1所示。
用Microsoft Office Excel 2013对试验测量得到的动边界环状缝隙区域的流速和压强数据进行处理,并且采用 Suffer 11.0、Origin 9.0、SPSS 21.0等软件对所采集数据进行统计分析。
1.3 试验方案与测点布置
筒装料管道水力输送动边界环状缝隙流的几何参数包括管道输送流量、管道车荷载、环状缝隙长度与环状缝隙宽度等[22]。本文选择了4种动边界环状缝隙宽度作为主控制因子,即0.025、0.02、0.015以及0.01 m,环状缝隙长度为0.1 m,管道车荷载为800 g,管道内部输送流量为50 m3/h。根据动边界环状缝隙的宽度值,本文所选择的管道车的料筒直径对应为0.05、0.06、0.07以及0.08 m,管道车料筒长度为0.1 m。
动边界环状缝隙区域的边界包括管道车动边界与管道静边界2部分。本文所研究的管道车动边界对管道车的真实边界进行了一定的简化,管道车动边界是指管道车圆柱侧壁面,不包括管道车支撑体和万向滚珠。管道静边界为管道车料筒动边界所对应的管道壁面局部区域。根据本文对环状缝隙区域边界的定义,可以得到动边界环状缝隙区域的整体结构为环形柱状体。
本文的试验测试段位于管道试验平台平直管段的中间位置,全长为5.8 m,其距离下游平弯管段的进口断面为2.7 m,且距离上游的管道车制动装置为4.7 m。试验测量时环状缝隙区域的中心距管道车的制动装置为7.2 m,如图1所示。


注:1¢~7¢表示7个压强测点位置,2#~4#表示3个流速测试断面。
2 数值模拟方法
2.1 控制方程与紊流模型
将流体假设为不可压缩的黏性流体,则时均连续方程和Reynolds方程[23]如下:


RNG-紊流模型对于分离流、二次流以及旋流等复杂的流场计算具有显著的优势[24],为此本文采用了由Yakhot和Orzag所提出的RNG-紊流模型对筒装料管道水力输送技术中动边界环状缝隙流的水力特性进行计算。RNG-紊流模型中湍动能方程和湍动耗散率方程[25]如下:


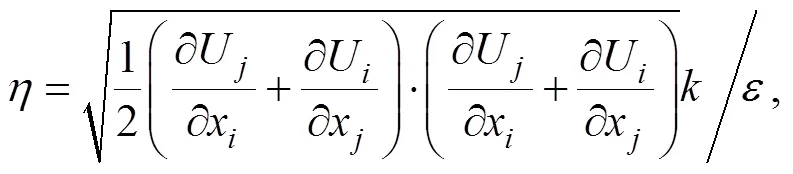
。
计算环境压力为1个标准大气压,流体密度为 1 000 kg/m3,流体动力黏度为0.001 031 9 Pa·s,计算中考虑重力对管道流体的影响。
2.2 几何模型创建与网格划分
本文采用Gambit 2.4.6软件创建了筒装料管道水力输送动边界环状缝隙流的几何模型。几何模型是由管道车与平直输送管道2部分所组成,几何模型结构如图3所示。

注:AB表示几何模型的进口断面,CD表示几何模型的出口断面,E表示管道车模型。
平直输送管道几何模型的全长为5.8 m,模型直径为0.1 m,该模型与图1中试验平台的试验测试段完全一致。为了提高数值模拟的计算准确度,本文将平直输送管道又分成了3个直管段部分,进口管段0.5 m(考虑到紊流的充分发展)、运动管段4.8 m(管道车中心的运移长度)以及出口管段0.5 m(考虑到管道车动边界运移对几何模型出口压力的影响)[26]。管道车几何模型与管道车实体模型一致,管道车料筒直径分别为0.05、0.06、0.07以及0.08 m,管道车料筒长度为0.1 m。管道车支撑体结构是由细圆柱体、薄六面体所组成,支撑体直径为0.01 m,支撑体高度为0.02 m,薄六面体的尺寸为0.01 m´0.015 m´0.001 m。万向滚珠的结构为半球形结构,该结构安装在靠近平直输送管道的一侧的支撑体末端。本文以几何模型进口边界的中心作为几何模型的坐标原点,为此管道车运移的初始位置中心坐标为(0.0 m,0.0 m,0.5 m)。
考虑到管道车外观结构的复杂性,本文采用了非结构化的四面体网格对几何模型进行了体网格加密。一般而言,计算域的内部网格划分的尺寸越小,其计算结果就越精确,但是计算量将会增大。为了获得理想的体网格尺寸,本文对4种动边界环状缝隙宽度的几何模型计算域的内部体网格尺寸进行网格无关性检验[27],如表1所示。
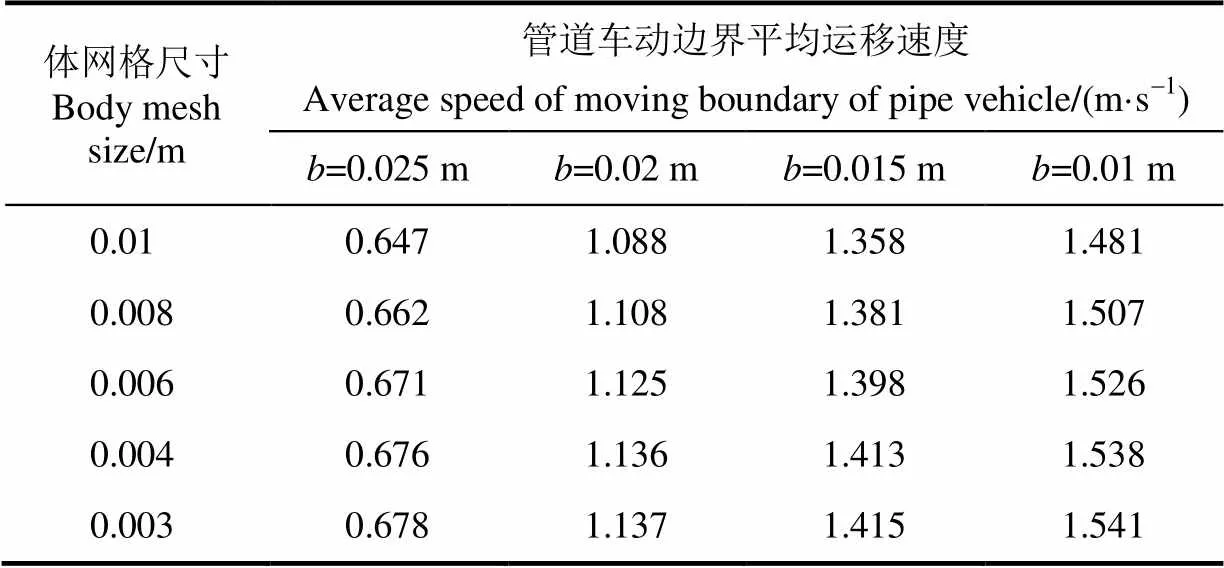
表1 网格无关性检验
注:表示动边界环状缝隙宽度。
Note:represents width of cyclical slit flow with moving boundary.
根据表1的网格独立性检验结果,可以得出由0.003 m体网格尺寸与0.004 m体网格尺寸所计算得到的4种环状缝隙宽度条件下管道车动边界平均运移速度的相对误差分别不超过0.32%、0.11%、0.14%和0.21%。当体网格尺寸小于0.004 m时,体网格尺寸对于管道车动边界平均运移速度的影响效果基本可以忽略不计。为此,在综合考虑计算机计算效率以及流场求解精度的前提下,本文选择的几何模型体网格尺寸设置为 0.004 m。为了提高输送管道和管道车的近壁面区域流场的计算精度,本文还采用边界层加密与局部面网格加密相结合的辅助加密方法。考虑到管道车动边界支撑体结构,管道车壁面的局部面网格划分为三角形结构,其具体尺寸为0.001 m。图4是以料筒直径为0.06 m的管道车为例,对管道车动边界在初始时刻的几何模型计算域进行的网格划分。

图4 动边界环状缝隙流几何模型网格划分示意图
2.3 边界条件与数值计算
Fluent数值模拟中所设定的边界条件如下:
1)如图1所示,几何模型进口边界对应试验测试段的1#断面,进口边界()选择流速入口(velocity-inlet)边界条件,其中紊流参数根据试验条件进行计算求解。几何模型输送管道的流量为50 m3/h,实测流体水温19℃,根据雷诺数计算公式得到管道雷诺数为171 367,该数值大于2 320,因此得到管道内为紊流工况。其他紊流参数包括湍流强度为0.035 5,湍流动能为0.005 9 m2/s2,湍流耗散率为0.010 6 m2/s3。为了提高几何模型的求解精度,模拟时根据该断面实际测量的3维流速,编写了相应的UDF(User-Defined Function)函数对几何模型进口边界的3维流速分布进行了定义。
2)如图1所示,几何模型出口断面对应试验测试段的5#断面,出口边界()选择压力出口(pressure-outlet)边界条件,采用该断面的压强实测值对几何模型的出口边界处的压强进行设置,本文中出口断面的压强值为8.1 kPa。
3)平直输送管道边界(、)采用无滑移边界条件,近壁面区域采用标准壁面函数法[28]进行处理。

为了提高动边界环状缝隙流的计算精度,本文还对于管道车动边界作出了如下的处理:


3)管道车在输送管道几何模型起始位置的初始运移速度采用高速摄像机对管道车在该断面处的瞬时速度的实测值进行定义。
本文采用PISO速度—压强耦合算法,该耦合算法对流场中的压强场进行2次校正,提高了瞬态流场的求解精度。由于控制方程各项的离散格式精度对计算结果影响很大,为此本文在已有研究成果的基础上合理的选择了控制方程各项的离散格式[32]。为了减少数值扩散,计算过程中,Reynolds方程、湍动能方程和湍动耗散率方程中的对流项选择二阶迎风离散格式,时均连续性方程中的压力项选择PRESTO!离散格式。本文非稳态模拟采用时间步长为10-5s,并且控制方程各项的离散格式收敛残差设置为10-4。
3 结果与分析
3.1 管道车动边界运移速度模拟与验证
图5为不同环状缝隙宽度条件下,管道车动边界在平直管段内部运移过程中瞬时速度的模拟值与试验值的对照图。

图5 管道车动边界瞬时运移速度的模拟值与试验值
从图5中可以得到:
1)模拟值与试验值一致,相对误差不超过1.3%。
2)管道车动边界在运移过程中瞬时运移速度基本围绕某一恒定速度以微小的幅度波动变化,可以认为管道车动边界在平直管段内的运移为恒定运动。
3)管道车动边界瞬时速度呈无规则变化趋势。原因是流体脉动压强的无规则波动将引起管道内部流体对管道车动边界的瞬时荷载产生波动变化,从而引起管道车动边界的瞬时加速度发生变化。
4)随着环状缝隙宽度的减小,管道车动边界的平均运移速度将逐渐增大。原因是环状缝隙宽度越小,表明管道车料筒直径越大,管道车动边界受到的流体的作用力越大,因此平均运移速度也就越大。
由于管道车动边界在平直管段的运移为恒定运动,因此可以近似将动边界环状缝隙流视为恒定流,即动边界环状缝隙区域的流动参数不随时间发生变化。为此,不需要研究管道车动边界在不同运动位置时的环状缝隙流水力特性,可以研究某一个典型瞬时运移位置即可。因此,本文着重选择了环状缝隙中心距管道车制动装置7.2 m位置处的环状缝隙流,从而进一步分析动边界环状缝隙流的水力特性。
3.2 环状缝隙流平均轴向速度模拟结果与验证
图6为不同环状缝隙宽度条件下,动边界环状缝隙流的平均轴向流速模拟值与试验值的对照图。从图6中可以得到:1)模拟值与试验值基本一致,最大相对误差不超过0.52%。2)当动边界环状缝隙宽度为0.015 m时,动边界环状缝隙流的平均轴向流速将达到最小。原因是动边界环状缝隙流的平均轴向流速为环状缝隙断面流量与环状缝隙断面面积之间的比值。当环状缝隙宽度小于0.015 m时,管道车动边界运移速度的降低幅度较大,引起了环状缝隙断面流量的变化率大于环状缝隙断面面积的变化率,使得动边界环状缝隙流的平均轴向流速呈现降低趋势。当环状缝隙宽度大于0.015 m时,管道车动边界运移速度的变化幅度较小,引起环状缝隙流量的变化率小于环状缝隙断面面积的变化率,使得动边界环状缝隙流的平均轴向流速将呈现增大趋势。
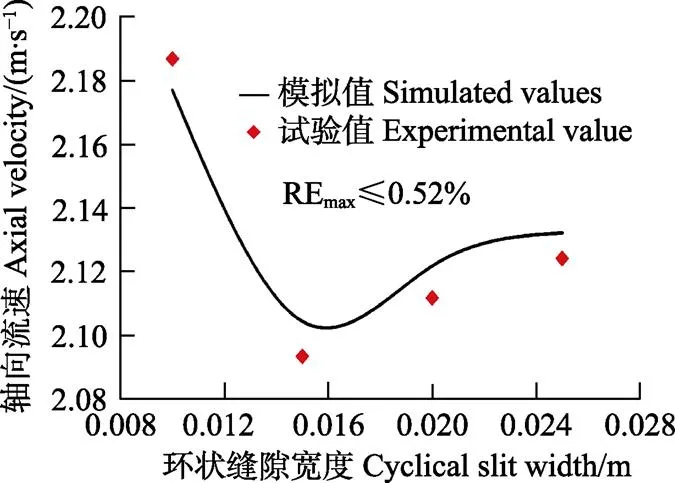
图6 不同环状缝隙宽度下动边界环状缝隙流轴向流速模拟与试验值
3.3 压强模拟结果与验证
图7为不同环状缝隙宽度条件下,管道车动边界中心位置运移到距几何模型进口断面2.5 m位置时的动边界环状缝隙区域管道静边界壁面处沿程压强的模拟值与试验值的对照图。
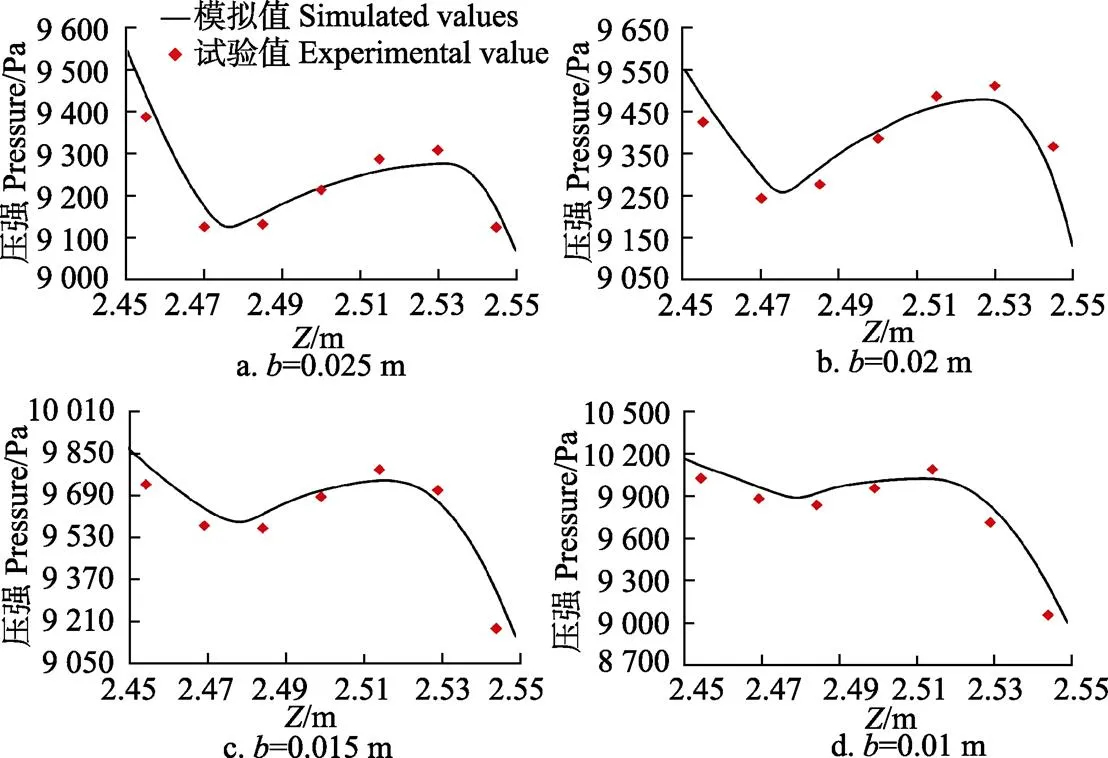
图7 不同宽度环状缝隙宽度下管道静边界壁面处沿程压强模拟值与试验值
从图7中可以得到:
1)模拟值与试验值基本一致,最大相对误差不超过1.3%。
2)动边界环状缝隙区域管道静边界沿程压强呈现出进口区域压强降低,中部区域压强升高,出口区域压强急剧降低的变化趋势。原因是在环状缝隙进口区域,管道车动边界的“直角凸起”引起环状缝隙流产生了边界层分离,而下游流体随即填补空腔区域,形成了旋涡能耗损失。在环状缝隙中部区域,环状缝隙流的发展逐渐稳定,引起环状缝隙的中间区域压强逐渐回升。在环状缝隙出口区域,环状缝隙流与管道车下游流体发生相互作用,导致环状缝隙流将能量传递给管道车下游流体,使得动边界环状缝隙区域的流体压强急剧降低。
3)随着动边界环状缝隙宽度的减小,环状缝隙进口区域压降幅度逐渐减小。原因是当环状缝隙宽度大于0.015 m时,随着环状缝隙宽度的减小,环状缝隙流轴向流速降低,引起环状缝隙流所形成的边界层分离区域减小,进而导致了旋涡能耗损失也随之减小。而当环状缝隙宽度小于0.015 m时,环状缝隙流将无法形成明显的边界层分离,使得该区域所产生了较小的旋涡能耗损失。总体分析,随着环状缝隙宽度的减小,环状缝隙进口区域的压降幅度将减小。
4)随着动边界缝隙宽度的逐渐减小,环状缝隙流中部区域的压强明显增加。原因是动边界环状缝隙中部压强反映了断面下游区域的管道车局部水头损失与管道车下游流体的沿程水头损失之和。随着环状缝隙宽度的减小,动边界环状缝隙流出口区域所引起的局部水头损失将逐渐增加,使得环状缝隙流中部断面区域压强将逐渐增大。
图8为不同环状缝隙宽度条件下,管道车动边界中心位置运移到距几何模型进口断面处2.5 m位置时管道车动边界水平断面处压强分布图。
从图8中可以得到:
1)从管道车动边界的上游流场过渡到环状缝隙区域过程中压强将明显降低。原因是环状缝隙区域内的流体平均流速高于管道内平均流速,由此环状缝隙区域的压强降低。
2)管道车动边界的下游流场存在明显的低压区,并且低压区的下游流场压强又再次升高。原因是环状缝隙出口处的边界层分离引起管道车动边界下游出现了旋涡损失,使得管道车动边界近壁面处压强逐渐降低。同时环状缝隙流与下游流体发生碰撞,该过程不但存在能量耗散还存在能量转化,即流体将能量传递给下游流体,因此下游流体的压强出现了再次升高的现象。
3)动边界环状缝隙进口区域的管道车动边界近壁面出现了明显的局部低压区。原因是由于管道车动边界表面存在“直角凸起”,使得环状缝隙流在管道车动边界近壁面产生了边界层分离。流体离开管道车动边界,下游流体随即回填空腔区域,该区域形成旋涡损失,从而导致了管道车动边界近壁面形成局部低压区。
4)环状缝隙中部区域压强分布沿径向基本一致,且管道车动边界近壁面区域压强略高于管道静边界近壁面区域压强。原因是在动边界环状缝隙的进口区域,环状缝隙流体产生了边界层分离现象。随后流体进入环状缝隙的中部区域向管道车动边界方向进行扩散,环状缝隙流与管道车动边界产生相互作用,引起流体的动能逐渐转化为压能,从而导致管道车动边界近壁面区域压强略高于管道静边界近壁面压强。但是由于流体的扩散角度一般较小,使得动边界环状缝隙的中部流场区域压强基本一致。
5)在环状缝隙流出口位置的流场区域,整体压强急剧降低。原因是环状缝隙流向管道车下游流场扩散过程中,环状缝隙流与管道车下游流体发生相互作用,环状缝隙流将动能转化为下游流体的压能,引起环状缝隙流的局部能耗损失。并且环状缝隙流在缝隙区域也产生了沿程水头损失,两者的共同作用促使环状缝隙的出口区域的整体压强急剧降低。
6)在环状缝隙流出口区域管道静边界的近壁面压强较低。原因是动边界环状缝隙流向管道车下游流场扩散的方向是从管道壁面指向管道圆心,因此管道静边界近壁面区域流体的压强较小。

注:a~d图中,左为上游,右为下游;e~h图中,上边界为管道静边界,下边界为管道车动边界。下同。
3.4 流速模拟结果与验证
图9为不同环状缝隙宽度条件下,管道车动边界中心位置运移到距几何模型进口断面处2.5 m位置时动边界环状缝隙2#、3#以及4#环状缝隙断面水平径向位置处轴向流速分布模拟值与试验值的对照图。
从图9中可以得到:
1)模拟值与试验值基本一致,最大相对误差不超过5.3%。
2)在动边界环状缝隙流场的2#断面处,管道车动边界近壁面的轴向流速呈先减小后增大的变化趋势。原因是环状缝隙流在管道车动边界的“直角突起”处产生了边界层分离现象,环状缝隙流离开管道车动边界向下游进行扩散,下游流体向上游方向流动回填空腔区域,使得该区域出现了明显的低流速区。

图9 不同宽度环状缝隙区域的各断面水平径向位置处轴向流速分布模拟值与试验值
3)动边界环状缝隙的2#断面位置处,随着环状缝隙宽度的减小,断面中间区域的轴向流速将从指数分布转变为抛物线型分布。原因是由于流体的黏滞性作用,环状缝隙流在近壁面区域呈现出与边界相同的运移速度,而在远离边界的区域将表现出相同的轴向流速分布。随着环状缝隙宽度的逐渐减小,引起环状缝隙区域仅存在近壁面区域的流场,从而使得在狭窄的环状缝隙宽度条件下形成的断面轴向流速将表现为抛物线形分布。
4)动边界环状缝隙的3#断面和4#断面处轴向流速分布基本一致。原因为在环状缝隙区域的3#断面和4#断面的动边界环状缝隙流进入了稳定发展的阶段,从管道车动边界到管道静边界的轴向流速沿径向呈现出先增加后减小的变化趋势。
图10为不同环状缝隙宽度条件下,管道车动边界中心位置运移到距几何模型进口断面处2.5 m位置时管道车动边界水平断面处轴向流速分布图。

图10 不同环状缝隙宽度条件下管道车动边界水平断面处轴向流速分布
从图10中可以得到:
1)从管道车动边界的上游流场过渡到环状缝隙区域的过程中轴向流速将逐渐升高。原因是环状缝隙区域内的流体平均流速均高于管道内平均流速。
2)管道车动边界的下游流场存在明显的低轴向流速区,而管道车动边界下游管道近壁面区域出现了明显的高流速区。原因是环状缝隙流在管道内扩散过程中与下游流体发生碰撞,从而导致动边界下游流场的出现了局部回流。局部回流在管道车动边界的作用下向管道近壁面区域进行高速扩散,引起了动边界下游流场管道近壁面区域的轴向流速增加。
3)环状缝隙进口区域的动边界近壁面存在明显的低流速区。原因是管道车上游流体进入环状缝隙区域时,在管道车动边界的“直角凸起”处产生了边界层分离现象。环状缝隙流与管道车动边界发生分离,下游流体随即回流填补主流所空出的流场区域,使得在管道车动边界的近壁面区域形成了局部低流速区。
4)环状缝隙宽度越大,环状缝隙流的轴向流速分布越均匀。原因是环状缝隙宽度越大,管道车动边界对环状缝隙流场的影响也越小,因此环状缝隙区域的轴向流速分布也越均匀。
5)随着环状缝隙宽度的减小,动边界近壁面所形成的低流速区的范围逐渐减小,且该区域逐渐偏向环状缝隙的进口区域。原因是当环状缝隙宽度大于0.015 m时,随着环状缝隙宽度的减小,环状缝隙流的平均流速也逐渐减小,从而引起管道车动边界产生的边界层分离程度降低,进而导致管道车动边界近壁面所形成的低流速区面积减小。当环状缝隙宽度小于0.015 m时,环状缝隙区域无法形成明显的边界层分离,因此动边界近壁面低流速区的范围也较小。总体分析,管道车动边界所形成的低流速区范围将随着环状缝隙宽度的减小呈现逐渐变小的变化趋势,并偏向环状缝隙的进口区域。
6)管道车动边界对环状缝隙区域的进口处轴向流速的影响范围约为0.02 m,管道车动边界对环状缝隙出口处的轴向流速的影响较小。因此,对于动边界环状缝隙流轴向流速的研究仅需要考虑进口区域的影响。
4 结 论
本文采用Fluent 12.0软件对不同环状缝隙宽度条件下筒装料管道水力输送的动边界环状缝隙流的水力特性进行了数值模拟与试验研究。结论如下:
1)模拟结果与试验结果基本一致,且最大相对误差不超过5.3%,研究表明采用数值模拟的研究方法分析筒装料管道水力输送技术中动边界环状缝隙流水力特性是可行的。
2)动边界环状缝隙流中管道静边界压强呈现出了进口区域压强降低,中部区域压强升高,出口区域压强再次急剧降低的变化趋势,并且管道车动边界的近壁面压强值略高于管道静边界的近壁面压强值。
3)随着环状缝隙宽度的逐渐增大,环状缝隙进口区域动边界近壁面所形成的低流速区的范围逐渐增大。并且随着环状缝隙宽度的逐渐增大,环状缝隙进口区域压降幅度将逐渐增大,而环状缝隙流中间区域的压强将明显降低。
4)动边界环状缝隙流的水力特性不仅受到管道车动边界相关结构参数的影响,而且还受到动边界上、下游管道流场的影响。
[1] 张春晋. 不同直径的管道车在平直管段内运移时的水力特性模拟研究[D]. 太原:太原理工大学,2015. Zhang Chunjin. The Simulation Resrarch on Hydraulic Characteristics of Moving Piped Carriage with Different Diameter at Horizontal Pipeline[D]. Taiyuan: Taiyuan University of Technology, 2015. (in Chinese with English abstract)
[2] 李永业,孙西欢,延耀兴. 管道车不同荷重时筒装料管道水力输送特性[J]. 农业机械学报,2008,39(12):93-96. Li Yongye, Sun Xihuan, Yan Yaoxing. Hydraulic characteristics of tube-contained raw material hydraulic transportation under the different loads on the piped carriage[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(12): 93-96. (in Chinese with English abstract)
[3] Kroonenberg H H. Mathematical model for concentric horizontal capsule transport[J]. Canadian Journal of Chemical Engineering, 1978, 56(5): 538-543.
[4] Sud I, Chaddock J B. Drag calculations for vehicles in very long tubes from turbulent flow theory[J]. Journal of Fluids Engineering, Transactions of the ASME, 1981, 103(2): 361-366.
[5] Azouz I, Shirazi S A. Numerical simulation of drag reducing turbulent flow in annular conduits[J]. Journal of Fluids Engineering, Transactions of the ASME, 1997, 119(4): 838-846.
[6] Khalil M F, Kassab S Z, Adam I G, et al. Turbulent flow around single concentric long capsule in a pipe[J]. Applied Mathematical Modelling, 2010, 34(8): 2000-2017.
[7] Polderman H G, Velraeds G, Knol W. Turbulent lubrication flow in an annular channel[J]. Journal of Fluids Engineering, Transactions of the ASME, 1986, 108(2): 185-192.
[8] Polderman H G. Design rules for hydraulic capsule transport systems[J]. Journal of pipelines, 1982, 3(2): 123-136.
[9] Tomita Y, Okubo T, Funatsu K, et al. Freight Pipelines: Proceedings of the 6th International Symposium on Freight Pipelines[M]. New York: Hemisphere Public Corporation, 1990: 273—278.
[10] Ulusarslan D, Teke I. Relation between the friction coefficient and re number for spherical capsule train-water flow in horizontal pipes[J]. Particulate Science and Technology, 2009, 27(5): 488-495.
[11] 李永业,孙西欢,李飞,等. 动边界同心环状缝隙流研究[J]. 农业机械学报,2009,43(3):230-234. Li Yongye, Sun Xihuan, Li Fei, et al. Cyclical slit flow of concentricity under the moving boundary condition[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 43(3): 230-234. (in Chinese with English abstract)
[12] 许贤良,朱兵,张军,等. 同心环形缝隙流理论研究[J]. 安徽理工大学学报:自然科学版,2004,24(3):40-42. Xu Xianliang, Zhu Bing, Zhang Jun, et al. The research of the concentric ring slit flow[J]. Journal of Anhui University of Science and Technology: Natural science, 2004, 24(3): 40-42. (in Chinese with English abstract)
[13] Yanaida K. Drag coefficient of capsules in turbulent flow inside a vertical pipe[J]. Journal of Pipelines, 1987, 6(3): 297-306.
[14] 张雪兰,孙西欢,李永业. 筒装料管道水力输送环隙流场特性试验研究[J]. 重庆交通大学学报:自然科学版,2014,33(2):75-78. Zhang Xuelan, Sun Xihuan, Li Yongye. Annulus flow field characteristics of the barreled material pipe hydraulic transportation[J]. Journal of Chongqing Jiaotong University: Natural Science, 2014, 33(2): 75-78. (in Chinese with English abstract)
[15] Zhang Xuelan, Sun Xihuan, Li Yongye. 3-D numerical investigation of the wall-bounded concentric annulus flow around a cylindrical body with a special array of cylinders[J]. Journal of Hydrodynamics, 2015, 27(1):120-130.
[16] 井元昊,郭向红,孙西欢,等. 管道车环状缝隙流水力特性[J]. 水电能源科学,2014,32(7):151-155. Jing Yuanhao, Guo Xianghong, Sun Xihuan, et al. Hydraulic characteristics of cyclical slit flow for piped carriage[J]. Water Resources and Power, 2014, 32(7): 151-155. (in Chinese with English abstract)
[17] 孙蕾,孙西欢,李永业,等. 不同直径比条件下同心环状缝隙流的水力特性[J]. 人民黄河,2014,36(11):110-113. Sun Lei, Sun Xihuan, Li Yongye, et al. Cyclical slit flow of concentricity under different diameter ratios[J]. Yellow River, 2014, 36(11): 110-113. (in Chinese with English abstract)
[18] 杨小妮,李永业,孙西欢. 旋流器在平直管道运行时的水力特性研究[J]. 水力发电学报,2015,34(2):98-102.Yang Xiaoni, Li Yongye, Sun Xihuan. Analysis on hydraulic characteristics of hydrocyclone in horizontal straight pipeline under operation[J]. Journal of Hydroelectric Engineering, 2015, 34(2): 98-102. (in Chinese with English abstract)
[19] 张琪琦,孙西欢,李永业. 圆柱体绕流环隙流场轴向流速及水力损失试验研究[J]. 长江科学院院报,2015,32(4):51-54,58. Zhang Qiqi, Sun Xihuan, Li Yongye. Experimental research on axial flow velocity and hydraulic energy consumption in annulus flow field around cylinder[J]. Journal of Yangtze River Scientific Research Institute, 2015, 32(4): 51-54, 58. (in Chinese with English abstract)
[20] 田济扬,白丹,于福亮,等. 基于Fluent软件的滴灌双向流流道灌水器水力性能数值模拟[J]. 农业工程学报,2014,30(20):65-71. Tian Jiyang, Bai Dan, Yu Fuliang, et al. Numerical simulation of hydraulic performance on bidirectional flow channel of drip irrigation emitter using Fluent[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 65-71. (in Chinese with English abstract)
[21] 李永业,孙西欢,李飞,等. 不同型号的管道车在管道中运移的水力特性[J]. 排灌机械工程学报,2010,28(2): 174-178. Li Yongye, Sun Xihuan, Li Fei, et al. Hydraulic characteristics of transportation of different piped carriages in pipe[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(2): 174-178. (in Chinese with English abstract)
[22] 王锐,孙西欢,李永业. 管道车在不同雷诺数条件下的输送特性[J]. 排灌机械工程学报,2011,29(4):343-346,358. Wang Rui, Sun Xihuan, Li Yongye. Transportation characteristics of piped carriage with different Reynolds numbers[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(4): 343-346, 358. (in Chinese with English abstract)
[23] 李贝贝,刘秀梅,龙正,等. 基于Fluent的节流阀油液空化流场数值分析[J]. 振动与冲击,2015,34(21):54-58. Li Beibei, Liu Xiumei, Long Zheng, et al. Simulation and analysis for cavitation flow field in a throttle valve based on Fluent[J]. Journal of Vibration and Shock, 2015, 34(21): 54-58. (in Chinese with English abstract)
[24] 张春晋,李永业,孙西欢. 明流泄洪洞水力特性的二维数值模拟与试验研究[J]. 长江科学院院报,2016,33(1): 54-60. Zhang Chunjin, Li Yongye, Sun Xihuan. Two-dimensional numerical simulation and experimental research of hydraulic characteristics in spillway tunnel with free water surface[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(1): 54-60. (in Chinese with English abstract)
[25] 柴博森,项玥,马文星,等. 制动工况下液力偶合器流场湍流模型分析与验证[J]. 农业工程学报,2016,32(3): 34-40. Chai Bosen, Xiang Yue, Ma Wenxing, et al. Analysis and experimental verification of turbulence models in flow simulation for hydrodynamic coupling under braking condition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(3): 34-40. (in Chinese with English abstract)
[26] Asim T, Mishra R, Abushaala S, et al. Development of a design methodology for hydraulic pipelines carrying rectangular capsules[J]. International Journal of Pressure Vessels and Piping, 2016, 146: 111-128.
[27] 梁东,弓志强,陈灿平,等. 轴流压气机引气后流场的数值模拟[J]. 航空动力学报,2017,32(2):446-454. Liang Dong, Gong Zhiqiang, Chen Canping, et al. Numerical simulation on flow field of axial compressor after bleeding[J]. Journal of Aerospace Power, 2017, 32(2): 446-454. (in Chinese with English abstract)
[28] 资丹,王福军,姚志峰,等. 大型泵站进水流场组合式导流墩整流效果分析[J]. 农业工程学报,2015,31(16): 71-77. Zi Dan, Wang Fujun, Yao Zhifeng, et al. Effects analysis on rectifying intake flow field for large scale pumping station with combined diversion piers[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 71-77. (in Chinese with English abstract)
[29] 舒敏骅,陈科,尤云祥,等. 动网格方法在螺旋桨非定常轴承力数值计算中的应用[J]. 中国舰船研究,2016,11(3):25-31. Shu Minhua, Chen Ke, You Yunxiang, et al. Application of the dynamic mesh method in the numerical simulation of unsteady bearing forces of a propeller[J]. Chinese Journal of Ship Research, 2016, 11(3): 25-31. (in Chinese with English abstract)
[30] Cao Wanpeng, Bai Wei, Che Rensheng. 6-DOF motion and center of rotation estimation based on stereo vision[J]. Chinese Journal of Mechanical, 2008, 21(2): 87-92.
[31] 黄剑峰,张立翔,杨松,等. 水轮机槽道内导叶动态绕流水力特性大涡模拟分析[J]. 农业工程学报,2017,33(4):125-130. Huang Jianfeng, Zhang Lixiang, Yang Song, et al. Analysis on hydraulic characteristics of dynamic flow around vane in hydro-turbine channel using large eddy simulation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 125-130. (in Chinese with English abstract)
[32] 苏华山,陈从平,赵美云,等. 泵轮轴向振动条件下高速液力耦合器特性[J]. 农业工程学报,2017,33(7):51-57. Su Huashan, Chen Congping, Zhao Meiyun, et al. Characteristics of high speed hydraulic coupler under pump wheel axial vibration conditions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(7): 51-57. (in Chinese with English abstract)
张春晋,孙西欢,李永业,张学琴. 筒装料管道水力输送动边界环状缝隙流水力特性数值模拟[J]. 农业工程学报,2017,33(19):76-85. doi:10.11975/j.issn.1002-6819.2017.19.010 http://www.tcsae.org
Zhang Chunjin, Sun Xihuan, Li Yongye, Zhang Xueqin. Numerical simulation of hydraulic characteristics of cyclical slit flow with moving boundary of tube-contained raw materials pipelines hydraulic transportation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 76-85. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.19.010 http://www.tcsae.org
Numerical simulation of hydraulic characteristics of cyclical slit flow with moving boundary of tube-contained raw materials pipelines hydraulic transportation
Zhang Chunjin1, Sun Xihuan1,2※, Li Yongye1, Zhang Xueqin3
(1.030024,;2.030600,; 3.250200,)
In order to solve effectively the problems of lower transport efficiency and higher utilization cost during the process of the long-distance transportation for the agricultural products, a kind of agricultural mechanical transport mode having a wide and great application prospect is proposed and known as the technique of tube-contained raw materials pipelines hydraulic transportation. The technique of tube-contained raw materials pipelines hydraulic transportation is the freight transportation mode that uses a fluid to suspend (float) and pull (drive) the pipe vehicle filled with the agricultural products from one location to another through a pressurized pipeline. According to the kinetic mechanism of the pipe vehicle, the mathematical models of the cyclical slit flow with the moving boundary under the different cyclical slit widths in the technique of tube-contained raw materials pipelines hydraulic transportation were established in this paper. The mathematical models were solved by adopting the RNG-turbulent model, the 6DoF coupling model and the PISO algorithm of the commercial software Fluent. The effects of the cyclical slit width on the internal hydraulic characteristics of the flow velocity and the pressure in the cyclical slit flow with the moving boundary were obtained. At the same time, through a wide of experimental investigations, the cyclical slit flow with 4 widths of 0.025, 0.02, 0.015, 0.01 m respectively were studied by using the Laser Doppler velocimeter (LDV) when the pipe vehicle moved within the pipelines. The experiment was carried out in the parallel straight pipe section of the test piping system, whose the control flow was 50 m3/h, carrying the loading of 800 g. The flow field characteristics such as the instantaneous velocity of the pipe vehicle with the moving boundary, the average axial velocity of the cyclical slit flow, the pressure distributions through the static wall of the pipeline and the velocity distributions of several typical sections were obtained. Comparing with the numerical results and experimental results, it was shown that the simulated results and the experimental results on the instantaneous velocity of the pipe vehicle with the moving boundary, the pressure distributions and the velocity distributions of the cyclical slit flow in the technique of the tube-contained raw materials pipelines hydraulic transportation were in substantial agreement, and the maximum relative error did not exceed 5.3%, which further indicated that using the commercial software Fluent was feasible for solving the hydraulic characteristics of the cyclical slit flow with the moving boundary in the technique of tube-contained raw materials pipelines hydraulic transportation; The overall pressure of the cyclical slit flow with the moving boundary within the pipelines showed a decreasing trend at the inlet of the cyclical slit areas, an increasing trend in the central location of the cyclical slit areas and a precipitous decline trend again at the outlet of the cyclical slit areas along the static boundary of the pipeline. The near-wall pressure of the moving boundary of the pipe vehicle was slightly higher than that of the static boundary of the pipeline. With the increasing of the cyclical slit width, the range in distributions of the low-velocity areas formed by the near-wall of the moving boundary at the inlet of the cyclical slit space increased gradually. As the cyclical slit width increased, the pressure drop increased gradually at the inlet of the cyclical slit areas while the pressure drop at the central location of the cyclical slit areas decreased significantly. The hydraulic characteristics of the cyclical slit flow with the moving boundary was affected not only by the structural parameters of the pipe vehicle, but also by the flow field of the upstream and the downstream of the pipe vehicle with the moving boundary within the pipelines. The study of this paper not only improved the relevant theories of the cyclical slit flow with the moving boundary, but also provided a feasible method for further study on the hydraulic characteristics of the cyclical slit flow with the moving boundary in the technique of tube-contained raw materials pipelines hydraulic transportation.
computational fluid dynamics; pressure; velocity; tube-contained raw materials pipelines hydraulic transportation; cyclical slit flow; moving boundary; hydraulic characteristics; pipe vehicle
10.11975/j.issn.1002-6819.2017.19.010
S377
A
1002-6819(2017)-19-0076-10
2017-03-26
2017-08-10
国家自然科学基金项目(51179116,50579044,51109155)
张春晋,男,山西平遥人,博士生,主要从事流体力学及流体机械研究。Email:zhangchunjintyut@163.com
※通信作者:孙西欢,男,山西临猗人,教授,博士生导师,主要从事工业水力学研究。Email:sunxihuan@tyut.edu.cn

