固定直径树的距离平方和问题
赵红锦,耿显亚
(安徽理工大学 数学与大数据学院,安徽 淮南 231001)
固定直径树的距离平方和问题
赵红锦,耿显亚*
(安徽理工大学 数学与大数据学院,安徽 淮南 231001)
定义图G中所有点对间的距离的平方和为,其中dG(u,v)为图G中任意顶点u,v之间的距离,LG(v)表示图G中点v到其它点的距离的平方和。在所有直径为d的n顶点树中分别确定使S(G)最小和第二小的树。
树;悬挂点;直径
1947年Harold Wiener引入了第一个化学指标(现称为Wiener指标)并发表了一系列的文章力证了有机化合物分子图的Wiener指标与分子化合物的一系列物理化学指标间有着密切联系。文中的图均为树图,与树的Wiener指标相关文章见文献[1-6]。近来许多学者将研究目标放在寻找具有最小和第二小指标值所对应的图上,并取得了一些成果见文献[1,7,8],且在Wiener指标之后引入了一个新指标S(G),其定义如下:
令S=S(G)为图G中所有点对间距离的平方和,表示为

其中dG(u,v)为图G中任意顶点u,v之间的距离;LG(v)表示图G中点v到其它所有点的距离的平方和。该量是由Mustapha Aouchich和Pierre Hansen在[9]中引入并在专论中得以广泛研究。S(G)被用于距离谱半径的研究,Zhou和Trinajstić利用阶数n证明了距离平方和S(G)的上界,见[10-12];并在只使用S(G)的情况下确定了图的距离谱半径的下界。作为它的延续,该文中确定在集合Tn,d(3≤d≤n-3)中使S(G)最小所对应的树。
文中所有的图都是简单且有限的。G=(VG,EG)表示顶点集为VG边集为EG的图。G-v,G-uv分别表示删除图G中点v以及点v所关联的边和删除边uv(uv∈EG)所得到的图。类似地,G+uv表示在图G上添加边uv(uv∉EG),其中u,v∈VG。图G中与点v相邻的所有顶点的个数称为顶点v的度,表示为d(v)。悬挂点是度为1的顶点。顶点u,v之间的距离d(u,v)为连接顶点u,v之间最短路的边数。图G中任意两顶点之间距离的最大值为G的直径,记为d。距离DG(v()v∈V(G))即为v到其它顶点的所有距离和,而LG(v)为v到其它顶点的所有距离的平方和。文中未定义的符号和术语参见[13]。
树是连通的无圈图,令T是直径为d的n个顶点树。如果d=n-1,那么T≅Pn,即n顶点路;如果d=2,那么T≅K1,n-1,即n顶点星图。因此,在以下内容中,假设3≤d≤n-2。令Tn,d={T:T为直径为d的n顶点树,3≤d≤n-2}。
1 引理
首先给出在结果证明中可能用到的引理。
引理1[14]令H,X,Y是三个连通的,成对的不相交图。假设u,v是H的两个顶点,u′,v′分别是X,Y的一个顶点。分别连接v和v′、u和u′得到图G,连接v,v′,u′得到图,连接u,v′,u′得到图,那么S()<S(G)或S()<S(G)。
通过引理1,可得以下结论。
推论1 图G的任意两点v,u分别连接s,t个悬挂点的图Gs,t见图1,那么

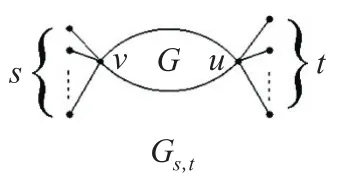
图1 图Gs,t示意图
令H1,H2是两个连通图,V(H1)⋂V(H2)={v},H1vH2是满足条件V(G)=V(H1)⋃V(H2),V(H1)⋂V(H2)={v}和E(G)=E(H1)⋃E(H2)的图。通过S(G)的定义可得以下结论。
引理2H为连通图,Tl是l个顶点的树且V(H)⋂V(Tl)={v}。那么S(HvTl)≥S(HvK1,l-1)
当且仅当HvTl≅HvK1,l-1时等号成立,HvK1,l-1中顶点v为K1,l-1的中心。
引理3G是n顶点图,v是G的一个悬挂点,u是与v相邻的顶点,那么

证明 由S(G)的定义,有

引理4G是连通的非平凡图,v是G中任一顶点。将两条长度分别为k,m(k≥m≥1)的路P=vv1v2…vk和Q=vu1u2…um的末端顶点连接到点v,可得,那么。

证明 利用引理3,可得
引理5 如果P=v0v1v2…vd是一条长度为d的路,那么

其中,1≤j≤d-1。此外,若1≤i<j≤d/2,则DP(vi)>DP(vj),LP(vi)>LP(vj);若d/2≤i<j≤d-1,则DP(vi)<DP(vj),LP(vi)<LP(vj)。
证明 依据D和L的定义,有
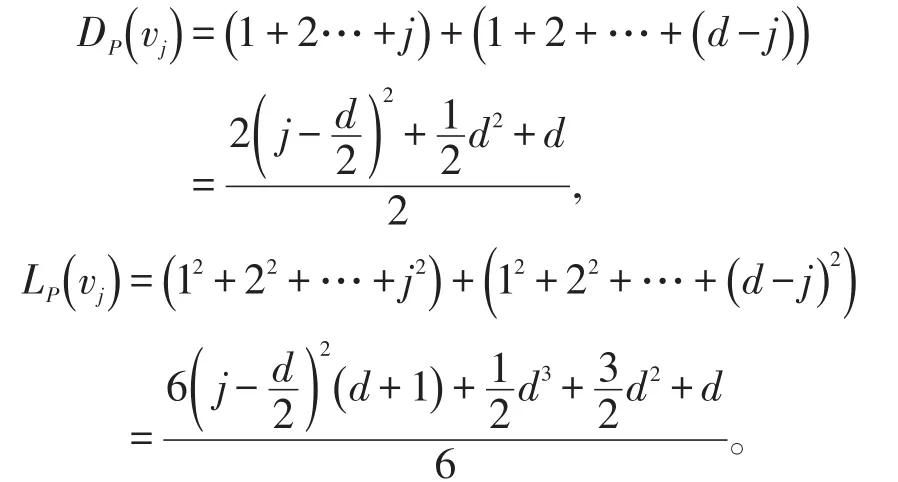
2 结论
该部分给出集类Tn,d(3≤d≤n-2)中最小和第二小的S(G)所对应的的树。为更好地阐述结论,需定义如下一些树,如图2。
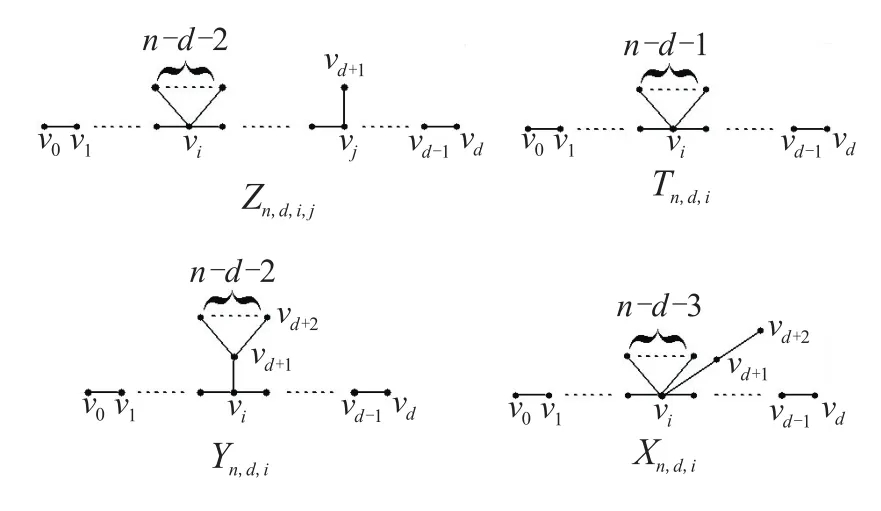
图 2 Zn,d,i,j、Tn,d,i、Yn,d,i、Xn,d,i示意图
Tn,d(p1,…,pd-1) 表示路Pd+1=v0v1…vd-1vd上任一点vi(1≤i≤d-1)连接pi个悬挂点所得n顶点树,且。
定义

那么Tn,d,i=Tn,d,d-i。
Tn-1,d,i的一个悬挂点(v0,vd除外)上连接一个悬挂点到得到Xn,d,i,Tn+2,d,i的一个悬挂点(v0,vd除外)上连接n-d-2个悬挂点到得到Yn,d,i,那么,Xn,d,i=Xn,d,d-i,Yn,d,i=Yn,d,d-i。
定义

证明 只需证明j=i-1的情况。依据引理4取v=vi,两条路分别为P=v0v1…vi,…vd,Q=vivi+1…vd,即可得以上结果。
注意到类似的不等式对于Xn,d,i和Yn,d,i同样成立。因此,当,有,当有。
通过引理6,可得以下结论。
引理7 假设3≤d≤n-3,那么
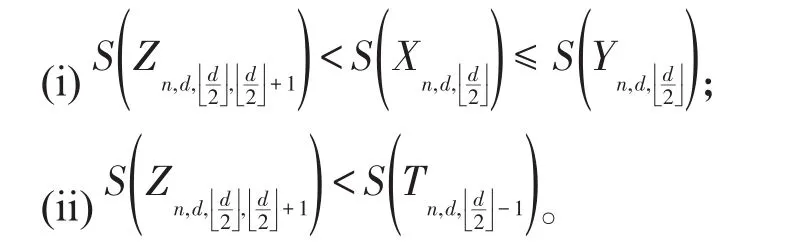
证明 由引理3,得
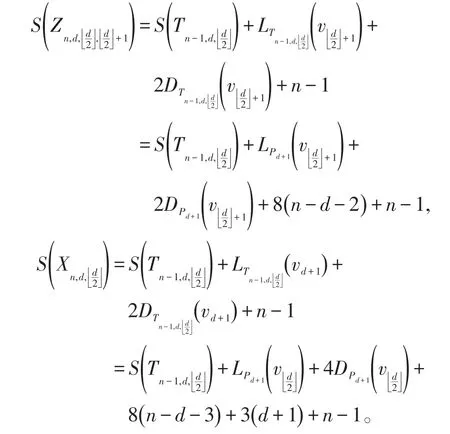
通过引理5,可得,当且仅当


因此,(i)式成立。
由引理5,知
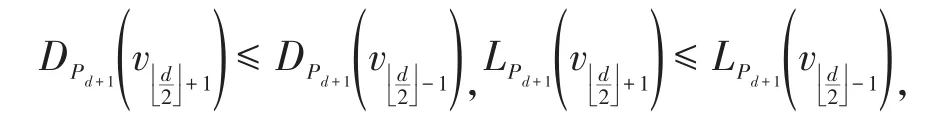
故由引理3,得
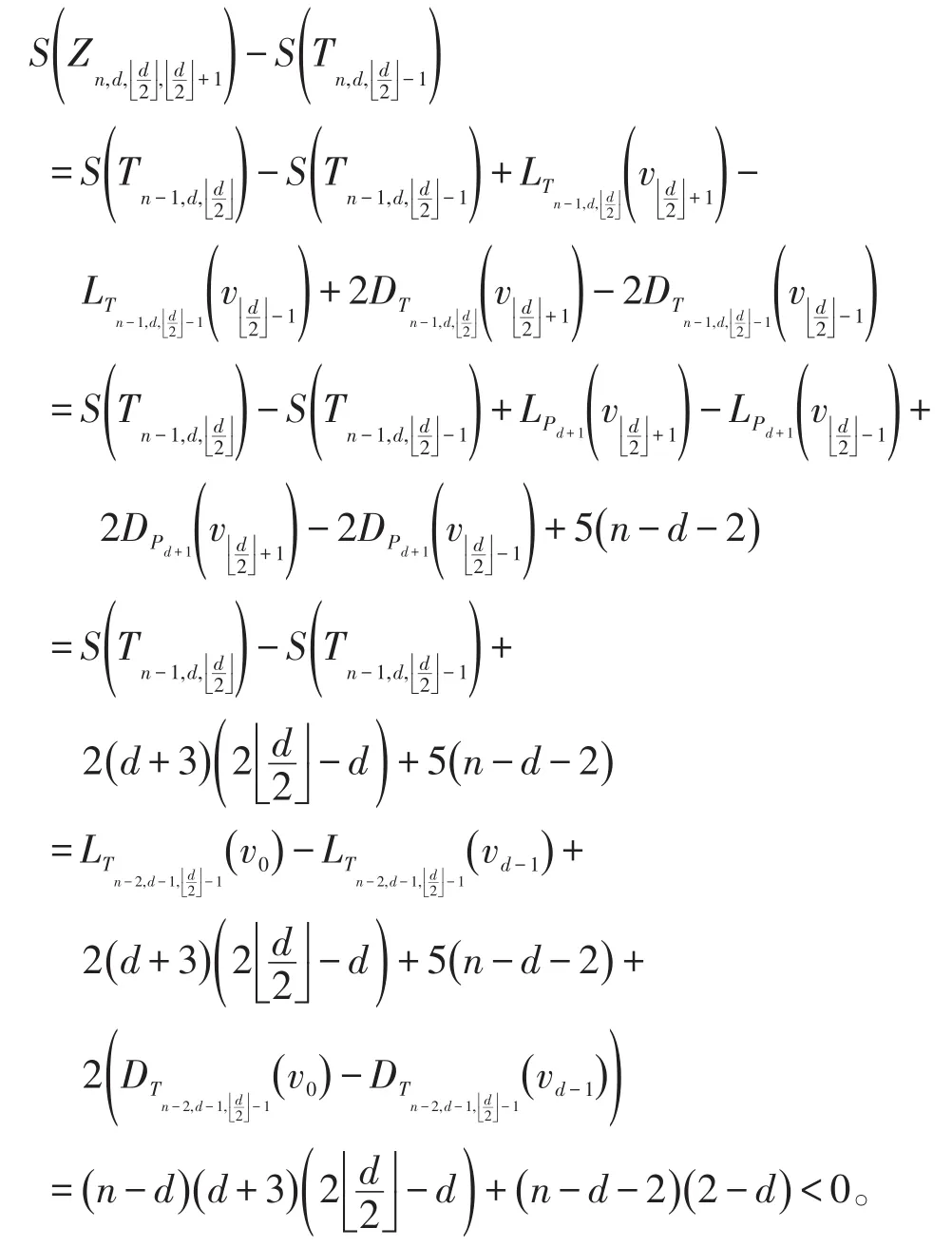
因此,(ii)成立。

证明 令T=Zn,d,i,j,P=v0v1…vd-1vd是一条长为d的路,d(v0)=d(vd)=1,且vd+1是T中与vj相邻的一个悬挂点,所选T是使S(T)最小的树。首先给出以下事实。

证明 注意到Zn,d,i,j-vd+1≅Tn-1,d,i。如果,那么由引理3和5得

证明 注意到Zn,d,i,j-vd+1≅Tn-1,d,i。如果,那么由引理3和6,可知
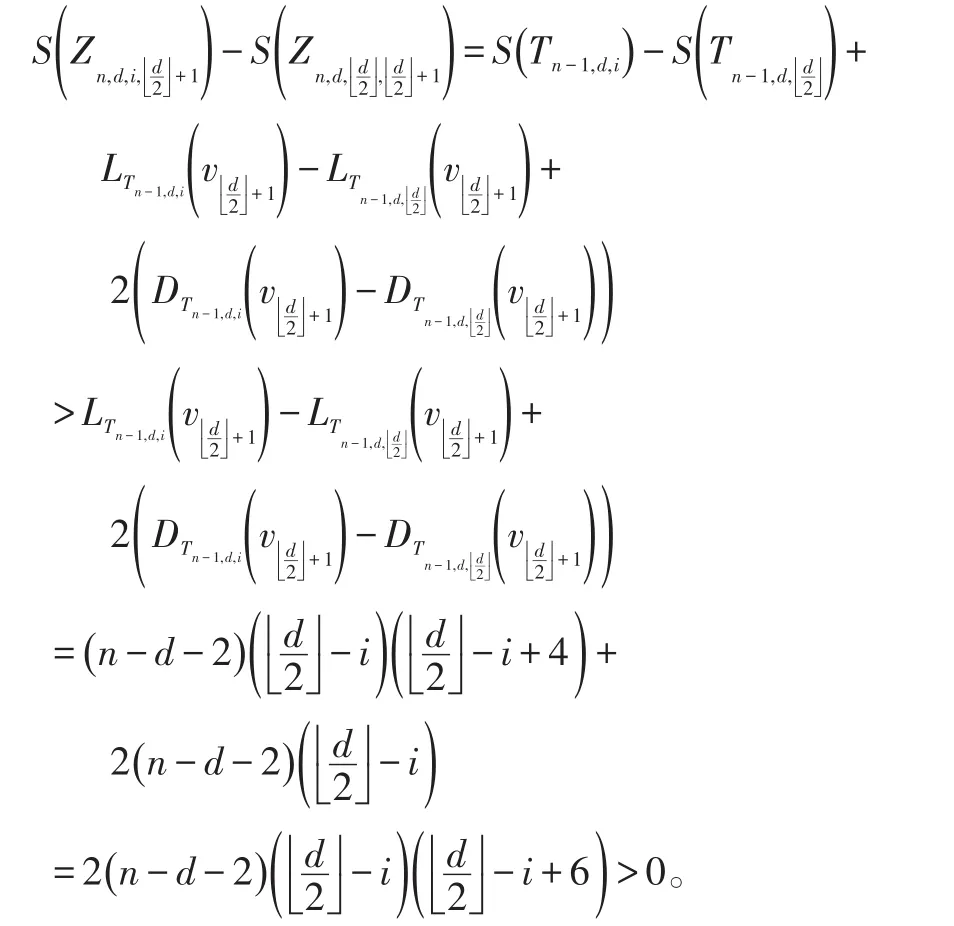
通过事实1,2,3,引理得证。
证明 令Pd+1=v0v1…vd-1vd是T中长为d的路且d(v0)=d(vd)=1,

由于n≥d+3,Vd≠ϕ。考虑如下两种情况。
情况1 |Vd|≥2。
这种情况下,首先得到使S(T)≥S(T1)的树T1,T1≅Tn,d(p1,…,pd-1),由引理2知当且仅当T≅T1时等号成立。又T∉Tn0,d,存在pi,pj≠0,1≤i<j≤d-1。故由推论1可得树T2≅Zn,d,i,j使得S(T1)>S(T2),又由引理8,可得
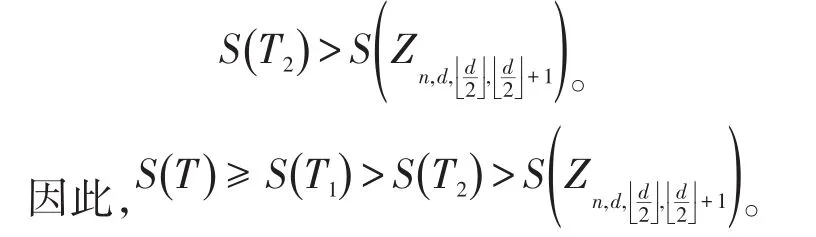
情况2 |Vd|=1。
在这种情况下,假设vi∈Vd,N(vi){vi-1,vi+1}={x1,…,xs},其中d(xj)≥2,1≤j≤r,且d(xr+1)=…=d(xs)=1,那么r≥1。令Ti(xj)是Ti(vi)的子树且包含xj,。由引理2,通过连接sj个悬挂点到xj(1≤j≤s)可由Td+s+1,d,i得到树T3,且S(T)≥S(T3)。通过推论1,可得树使得S(T3)≥S(T4)。如果,那么由引理7可得。如果,那么由引理7可得。
通过引理6,7和9,可得以下结果。
定理1 (i)集合Tn,d(3≤d≤n-2)中使S(G)最小的树为;
(ii)集合Tn,d(3≤d≤n-3)中使S(G)第二小的树为。
3 小结
文章将固定直径d(3≤d≤n-3)的树划分为四种图类,利用指标S(G)的定义和图类间的转化关系,最终得出在固定直径的树中使S(G)最小和第二小的分别对应的树。今后可研究在该条件下使指标S(G)第三小时是否有唯一的树存在。
[1]Dobrynin A A,Entringer R,Gutman I.Wiener index of trees:theory and applications[J].Acta Applicandae Mathematicae,2001,66(3):211-249.
[2]Li S C,Song Y B.On the sum of all distances in bipartite graphs[J].Discrete Applied Mathematics,2014,169(22):176-185.
[3]Liu M H,Liu B L.On the variable Wiener indices of trees with given maximum degree[J].Mathematical and Computer Modelling,2010,52(9/10):1651-1659.
[4]Dobrynin A A,Gutman I,Klavžar S,et al.Wiener index of hexagonal systems[J].Acta Applicandae Mathematica,2002,72(3):247-294.
[5]Fischermann M,Gutman I,Hoffmann A,et al.Extremal chemical trees[J].Zeitschrift Fur Naturforschung Section A-a Journal of Physical Sciences,2002,57(1/2):49-52.
[6]Gutman I,Potgieter J H.Wiener index and intermolecular forces[J].Journal of Serbian Chemical Society,1997,62:185-192.
[7]Ashrafi A R,Yousefi S.Computing the wiener index of a TUC 4 C 8(S)nanotorus[J].Match Communications in Mathematical&in Computer Chemistry,2007,57(2):403-410.
[8]Deng H Y.The trees on n≥9 vertices with the first to seventeenth greatest Wiener indices are chemical trees[J].Match Communications in Mathematical&in Computer Chemistry,2007,57(2):393-402.
[9]Aouchiche M,Hansen P.Distance spectra of graphs:A survey[J].Linear Algebra and Its Applications,2014,458(2):301-386.
[10]Zhou B,Trinajstić N.Mathematical properties of molecular descriptors based on distances[J].Croatica ChemicaActa,2010,83(2):227-242.
[11]Zhou B,Trinajstic N.On the largest eigenvalue of the distance matrix of a connected graph[J].Chemical Physics Letters,2007,447(4/6):384-387.
[12]Zhou B,Trinajstic N.Further results on the largest eigenvalues of the distance matrix and some distance based matrices of connected(molecular)graphs[J].Internet Electronic Journal of Molecular Design,2007,6(12):375-384.
[13]Bondy J A,Murty U S R.Graph Theory with Applications[M].Macmillan,1976:237-238.
[14]Liu H Q,Lu M.A unified approach to extremal cacti for different indices[J].MATCH-Communications in Mathematical and in Computer Chemistry,2007,58(1):183-194.
Sum of the squares of all distances in a tree with fixed diameter
ZHAO Hong-jin,GENG Xian-ya*
(School of Mathematics and Big Data,Anhui University of Science and Technology,Huainan Anhui232001,China)
Denote the sum of the squares of all distances between all pairs of vertices inGbywheredG(u,v)is the distance betweenuandvinGand the sum goes over all the pairs of vertices,LG(v)denotes the sum of the squares of all distances fromuinG.The trees with minimum and second-minimumS(G)among all the trees withnvertices and diameterdare obtained respectively.
tree;pendant vertex;diameter
O157.5
A
1004-4329(2017)03-005-05
10.14096/j.cnki.cn34-1069/n/1004-4329(2017)03-005-05
2017-03-17
国家自然科学基金(11401008,61672001);中国博士后科学基金(2016M592030)资助。
赵红锦(1990- ),女,硕士生,研究方向:图论及其应用。
耿显亚(1981- ),男,博士,副教授,研究方向:代数图论及其应用。Email:gengxianya@sina.com。