小波变换在大学生学业影响因素分析中的应用研究

高 鹏，谢 东，沙 君

（铜陵学院 电气工程学院，安徽 铜陵 244000）

小波变换在大学生学业影响因素分析中的应用研究

高 鹏，谢 东，沙 君

（铜陵学院 电气工程学院，安徽 铜陵 244000）

本文将小波变换应用于大学生学业成绩分析。通过不同班级学业成绩进行问卷调查，运用DB4小波对该数据进行小波变换，从而得到小波细节信号。同时，对该细节信号求方差，对得到的各组细节信号和方差数据进行比较，对不同班级出现的学业差异问题原因进行分析和研判。

小波变换；学业；影响因素；分析

教育的“十三五”规划明确将提高教育质量作为未来高等教育发展的主要方向。在校大学生学业水平高低就成为衡量高等教育质量水平高低的关键。目前较多高校的现状是，几乎相同高招分数进校学习的大学生，在经过学校的学习生活后，毕业时的学业成绩往往差异较大。研究该情况的论文也较多，分别从家庭背景、学校的纪律体系、教师的学术修养、班级文化和教学模式改革等方面进行了探究和分析[1-6]。目前对影响学业因素的分析主要还是用数理统计的方法来分析和研究[7-10]。本文将小波变换用于分析影响大学生学业成绩因素，对处理后的细节信号进行分析研究，从而得出各影响因素在大学生学业差异中的所占比重，为教育管理者更好为学生找准学习思路，帮助大学生提高学业水平提供有力的参考。

1 小波变换原理

小波变换是建立在傅里叶分析基础上的数据分析工具。相较于传统的傅里叶变换，小波变换可以从时域和频域上充分展示被分析对象的局部化特征，可以聚焦细节信号[11-12]。本文正是运用小波分析该特点，具体原理如下。

在不同尺度上，记L2(R)是定义在实数集上平方可积的空间。如φ(t)∈L2(R)满足允许性条件，则φ(t)称为可允许小波函数或基小波函数。通过基小波函数φ(t)的伸缩和平移，由连续小波得到可允许小波函数，其中，a,b∈R，a＞0。对于任意函数f(t)∈L2(R)，其可允许小波函数φa,b(t)的连续小波变换为

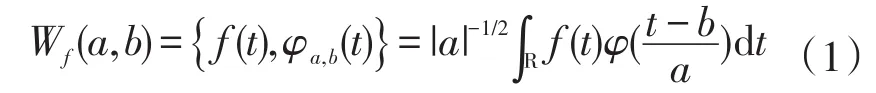
其中a表示伸缩尺度因子，b表示平移尺度因子，Wf(a,b)就成为小波系数，

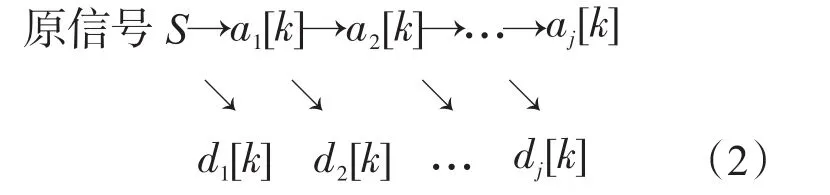
本文对原信号S分解得到细节信号dj[k]进行求方差运算。小波变换得到的细节信号的方差值越大，表明该组信号的离散程度越大和突变信号越多，而突变信号越多则表明该因素对该班级的成绩影响越大。

2 分析

2.1 分析对象

以某所地方性应用型本科高校的2个班级的一个学期的期末综合测评班级排名为分析研究对象，每个班级共有36名学生，其中A班由于整体学习较为优秀，被评为校级优良学风班，而B班则整体成绩一般。本文从班级整体的自觉上自习情况、旷课缺课情况、学习目标明确情况、寝室学习氛围、对本专业感兴趣情况等5个问卷调查方面来探究影响大学生成绩因素以及各影响因素所占的比重。

2.2 分析步骤

首先对这2个班级的同学进行问卷调查，问卷调查的内容为5题，分别是：1、本人是否能经常自觉上自习？能（0）、不能（1）；2、本人是否经常旷课？不是（0）、是（1）；3、本人对本科毕业后是否有明确的目标？有（0）、暂时没有（1）；4、本人所在寝室学习氛围如何？好（0）、一般（1）；5、本人是否对所学专业感兴趣？感兴趣（0）、一般（1）。本文设定出现利于学习的选择项输出为0，否则则输出1认定为个突变信号。问卷调查统计结果如表1、表2所示。

其次，按照班级综合测评的排名从班级从第一名排到最后一名，为了显出每个突变的1信号，在每个同学间均加入0信号，这样每个班级共有71个信号。

再次，将每个班级共得到的6组信号分别用DB4小波进行变换分析，得到每组共12个信号的细节信号。

最后，求出该12组细节信号的方差，对小波方差进行分析研究。

2.3 结果分析

首先对2个班级5个问题的总体问卷情况信号进行小波变换，得到的细节信号分别如图1所示。从图1可看出，对于有较多突变信号“1”的普通班B班经过小波变换得到的细节信号的离散程度较学风优良班的A班更大，具体数值如表3。

各问题小波变换的细节信号如图2～6所示。

图1 总体信号的细节信号

图2 第1个问题的细节信号

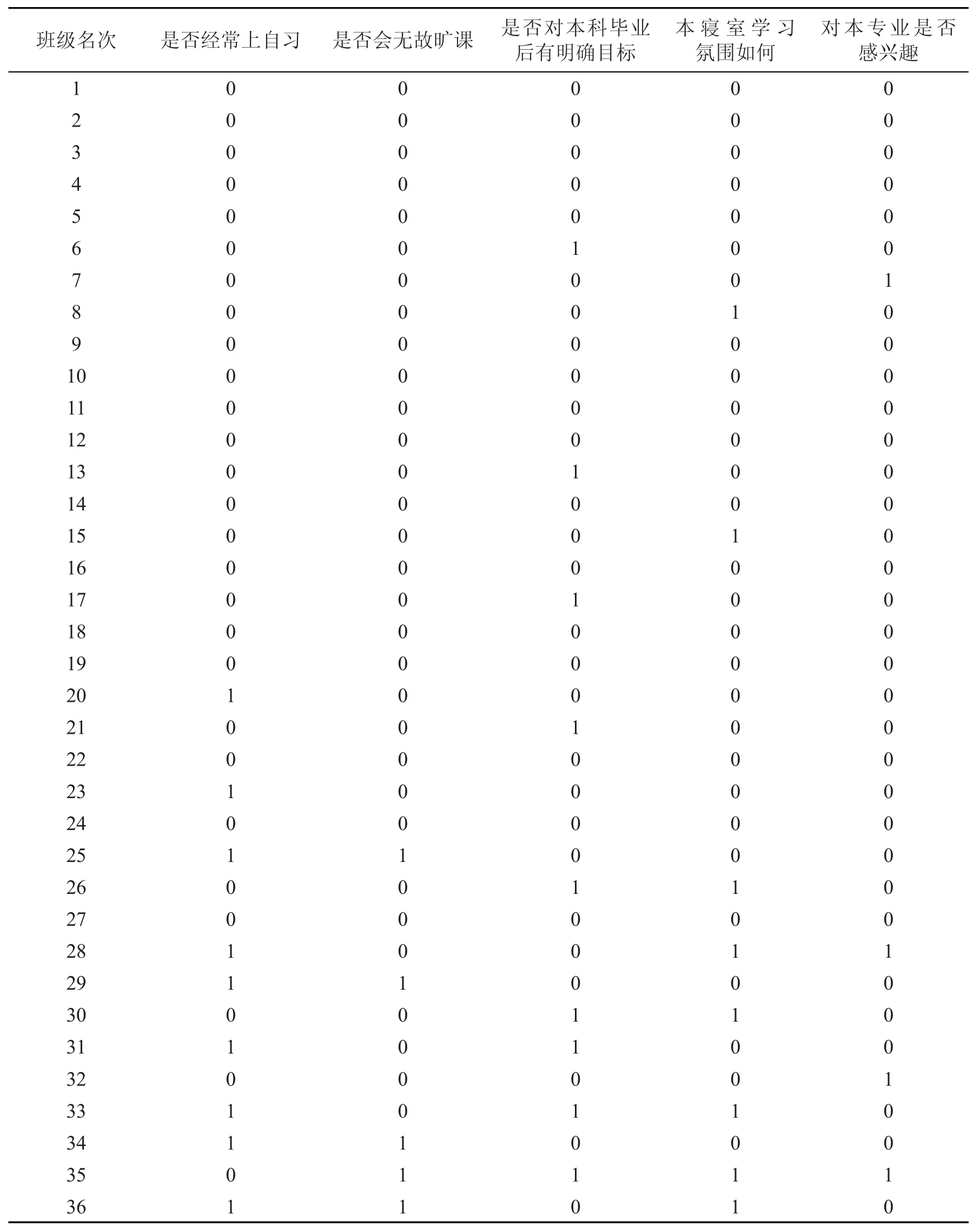
表1 A班问卷调查统计结果

表3和图7中可以看出，小波变换的细节信号的方差值越大，表明该组信号的离散程度越大和突变信号“1”越多，而突变信号越多则表明该因素对该班级的成绩影响越大。

从班级内部来看：对于优良学风班的A班，5个影响学生成绩的因素中的毕业后有无目标和是否能自觉上自习对该班学生影响最大；对于普通班B班毕业后有无目标、是否能自觉上自习和寝室学习氛围如何对该班学生成绩影响最大。从班级之间来看：优良学风班的A班的方差均比普通班的B班小，尤其是在平时是否旷课和对本专业感兴趣程度2个因素差别较大，表明本文列举出的5个影响学生成绩的因素对A班产生的突变信号较小，所以A班整体较之B班要优秀。

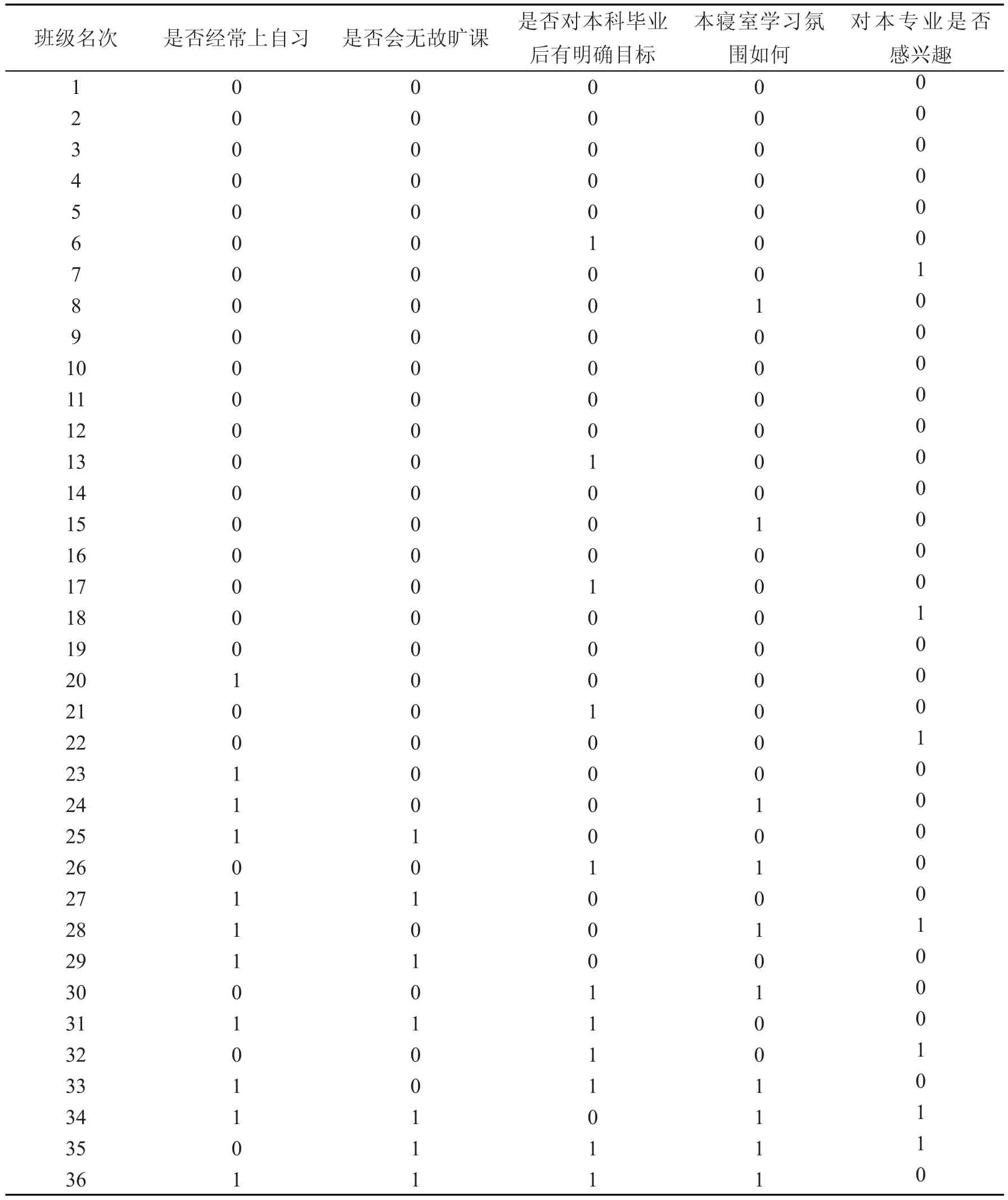
表2 B班问卷调查统计结果

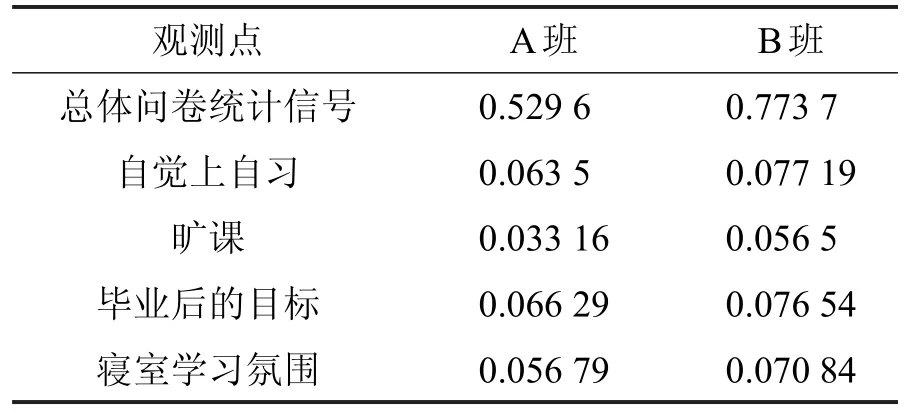
表3 小波细节信号方差表

3 结论

本文将小波变换分析引入到对大学生成绩影响因素的分析和研究。通过问卷调查得到信号数据，通过DB4小波分析处理后得到细节信号，并得出细节信号的小波方差。通过分析研究可以看出，小波分析可以较好的分析出影响班级成绩优劣的因素，可以为班级管理者更好的管理班级，帮助大学生提高学业水平提供有效的依据和支撑。

图3 第2个问题的细节信号

图4 第3个问题的细节信号

图5 第4个问题的细节信号

图6 第5个问题的细节信号

图7 A、B班级问卷5个问题小波细节信号方差图

[1]涂咏梅，徐彦坤.家庭因素对学生成绩影响的实证分析[J].统计与决策，2013,（2）：116-119.

[2]张咏梅，田 一，李美娟.学校背景因素和学生个体因素对学业成绩的影响的研究--基于大规模测试数据的多层线性模型分析[J].教育科学研究，2012,（04）：41-46.

[3]韩晓玲.基于NSSE-CHINA调查的大学生学习投入影响因素分析[D].南京：南京邮电大学，2014：10-12.

[4]张 苗，张 艳，刘 泉，等.在大学物理教学中引入探究型教学模式对学习成绩的影响[J].合肥师范学院学报，2014,32（6）：86-88.

[5]曹春春.家庭资本与大学生学习成绩关系的研究[D].芜湖：安徽师范大学，2013：20-25.

[6]何义芳，孙 侠，许占全.和谐班级文化对大学生行为的影响[J].中国医药导报，2006，3（22）：113-116.

[7]朱海林，宋承祥，刘 宏.基于支持向量机的教育质量评价研究[J].山东师范大学学报（自然科学版），2008，23（4）：4-6.

[8]赵友元.论教育过程中的非线性关系[J].教育探索，2001，（12）：53-54.

[9]李 雪.基于决策树算法的成绩分析系统[D].长春：长春理工大学，2010：14-19.

[10]刘爱萍.数据挖掘技术在高职院校学生成绩分析中的应用[D].泉州：华侨大学，2016：21-23.

[11]高 志.Matlab小波分析及应用[M].北京：国防工业出版社，2007：1-28.

[12]刘明才.小波分析及应用[M].北京：清华大学出版社，2005：1-138.

Application of wavelet transformation in academic factors of college students

GAO Peng,XIE Dong,SHAJun
(School of Electrical Engineering,Tongling University,Tongling Anhui244000,China)

This paper mainly introduces the wavelet transform into the analysis of college students'academic achievement，and questionnaires were obtained by conducting a questionnaire survey of the overall different grades of academic achievement，and the advantages of data detail can be obtained by wavelet transform.Wavelet transform is applied to the data using DB4 wavelet,and the wavelet detail signal is obtained，and the difference between the details of the signal，the comparison of the detailed signal and variance data of each group is carried out to analyze and judge the academic differences in different classes.

wavelet transform;academic achievement;influencing factors;analysis

TP183

A

1004-4329（2017）03-013-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）03-013-05

2017-04-21

安徽省科技厅自然科学基金面上项目（160805ME120）；铜陵学院校级项目（2015tlxy30）资助。

高 鹏（1984- ），男，硕士，讲师，研究方向：现代控制理论与应用。