“一类功能反应的食饵-捕食者两种群模型的定性分析”一文的注记
魏长城,林 记
(1.铜陵学院 数学与计算机学院,安徽 铜陵 244000;2.阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
“一类功能反应的食饵-捕食者两种群模型的定性分析”一文的注记
魏长城1,林 记2
(1.铜陵学院 数学与计算机学院,安徽 铜陵 244000;2.阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
本文对“一类功能反应的食饵-捕食者两种群模型的定性分析”中功能反应的食饵-捕食者系统重新进行了分析,构造了Dulac函数,利用Bendixson-Dulac定理,给出了系统极限环不存在性的结论,纠正了其中关于极限环存在定理。同时分析了系统在第一象限内轨线的拓扑结构。
捕食系统;Dulac函数;极限环;拓扑结构
2002年,文[1]对如下的系统

做了定性分析。经过分析,发现其中有些处理方法和结论值得商榷。

这里b>0,A0>0,A1>0。同时文[1]依据系统(2)的奇点(0,0)为鞍点,自然诱导出系统(1)的奇点是鞍点,进一步构造外境界线,利用Bendixson定理给出了系统极限环存在定理。但是忽略了在x=0处是不可导的。因此系统(1)和(2)仅在区域D={(x,y)|x>0,y∈R}上是等价的。因此,考虑到系统(1)的生物意义,本文限在区域上内研究,对文[1]反应的食饵-捕食者系统重新进行了分析,构造了Dulac函数,利用Bendixson-Dulac定理,给出了系统极限环不存在性的结论,纠正了文[1]中关于极限环存在定理。同时分析了系统在第一象限内轨线的拓扑结构。
1 系统(2)的奇点及性态
(1)有限远奇点分析
基于文[1],经过计算在上有奇点,当A1≥b时,在上有奇点。
引理1 当A1>b时,点为系统(2)的鞍点;当A1<b时,点为稳定结点;当A1=b时,点为高阶奇点,且为鞍结点;当A1>2b时,点为不稳定的结点(或焦点);当b<A1<2b时,点为稳定的结点(或焦点);当A1=2b时,点为中心。
证明 经计算,有

于是,当A1>b时,B1为鞍点;当A1<b时,有detJ1>0,trJ1<0和
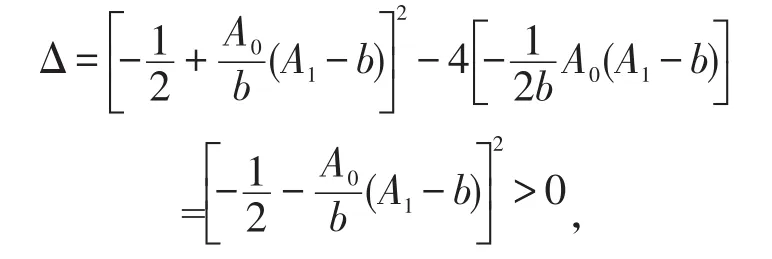
当A1=b时,此时detJ1=0,于是为高阶奇点。此时,对系统(2)做变换。变换以后的仍用x,y记之,于是模型变为
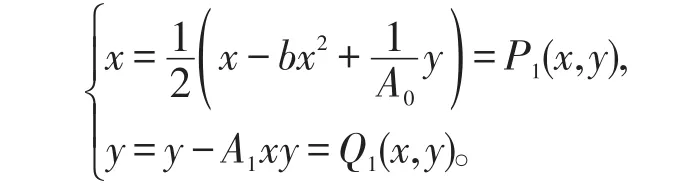




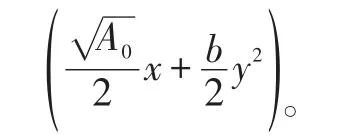
令上式的三次项为零,即

(2)无穷远奇点分析


令z=0,有u=0。故只有奇点C(0,0)。
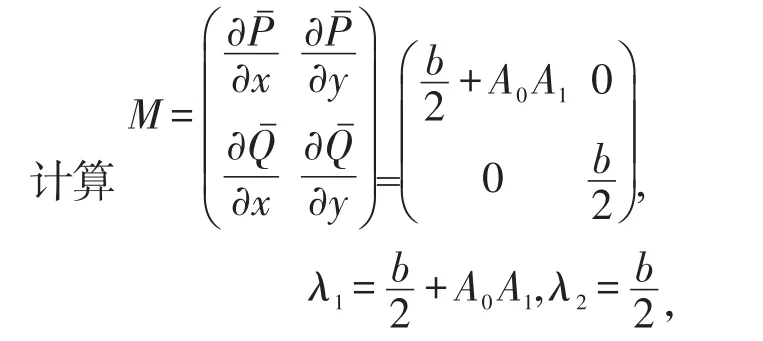
所以C(0,0)是不稳定结点。


研究奇点D(0,0):

做变换T:ξ=v,η=y+P2(x+y),由隐函数存在定理,在D(0,0)的充分小领域内,存在逆变换

计算得
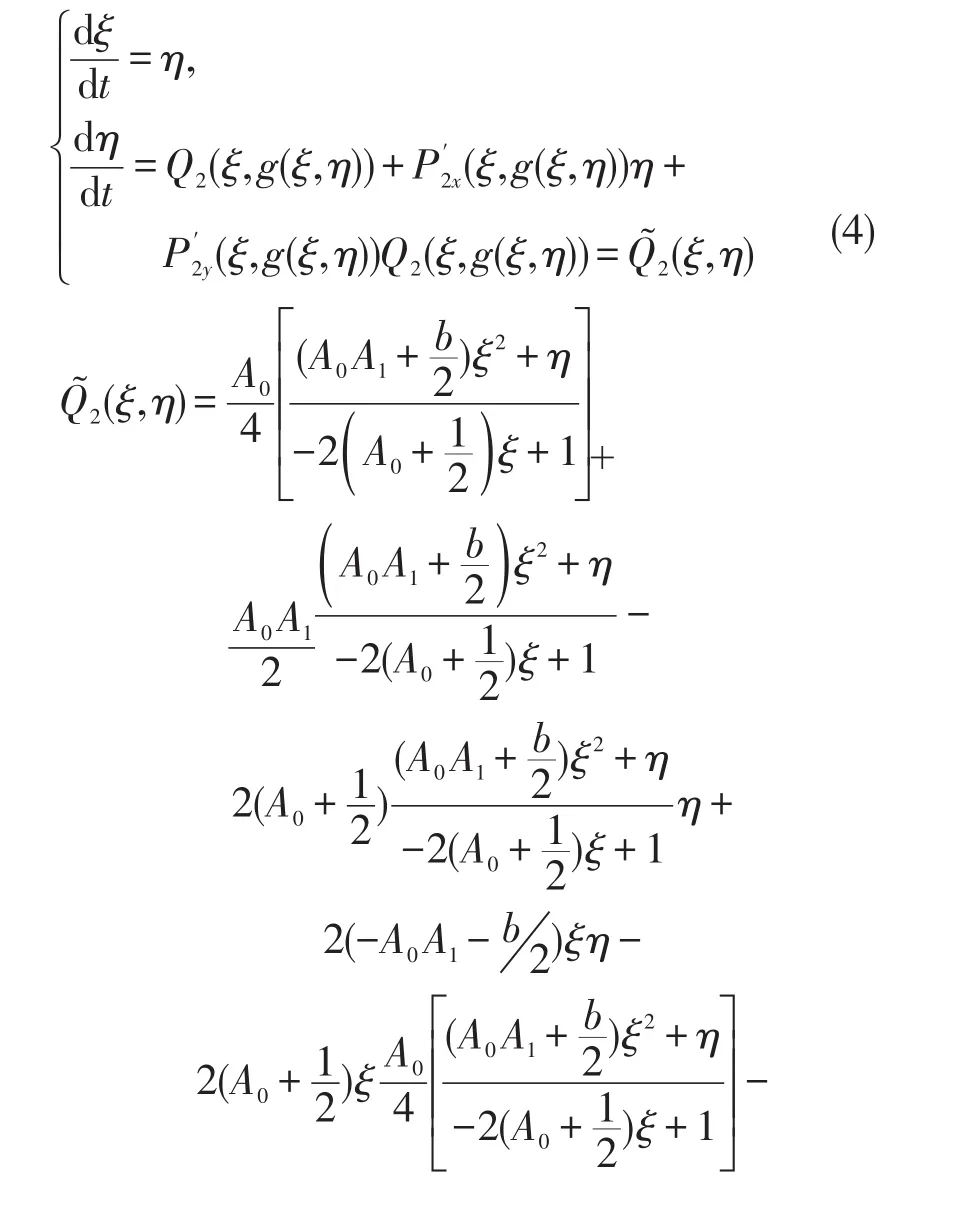

为了简单起见,将(4)式写为
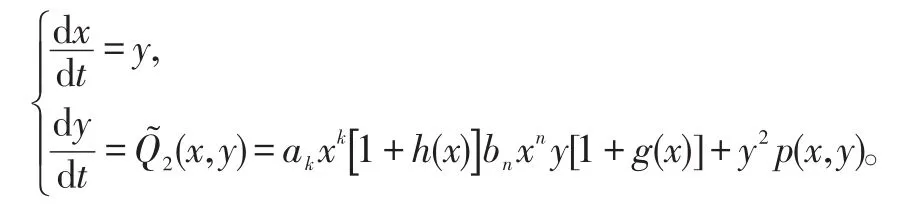
易知k=2,bn≠0,n<m,故是D(0,0)鞍结点。
2 极限环的不存在性定理
考虑方程
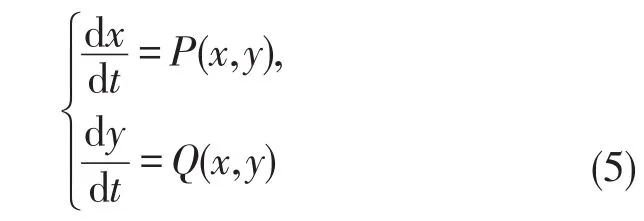
这里P,Q∈C1(G)。

定理 系统(2)在={(x,y)|x>0,y≥0}上不存在极限环。
证明 由于y=0是系统(2)的积分直线,所以仅需在={(x,y)|x>0,y>0}上考虑极限环的存在和不存在问题。
构造Dulac函数,令B(x,y)=xαyβ(x>0,y>0),这里待定α,β。计算
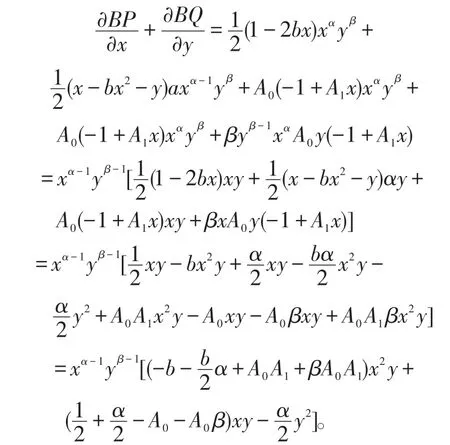
考虑线性代数方程
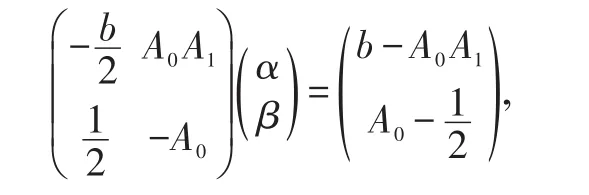

有唯一解。进一步当A1≠2b时,有α≠0,于是有
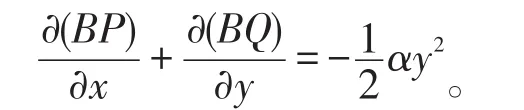
利用引理2知系统(2)在上不存在极限环。
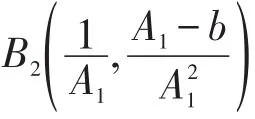

定理得证。
3 旋转向量场
考虑系统(2),易见只有参数A0变动时向量场(X(x,y,A0),Y(x,y,A0))的奇点不变。
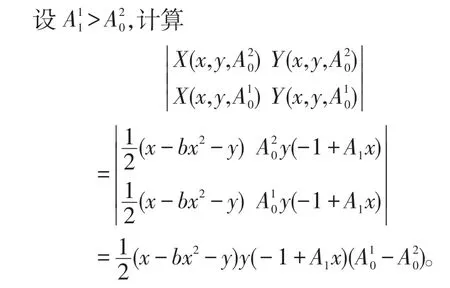
于是对任意点P(x,y)∈,并不能保证上式恒大于0或恒小于0。故系统(2)不是广义旋转向量场。
4 系统(2)的全局结构
基于前面结论,给出了系统(2)的全局结构,如图1所示。
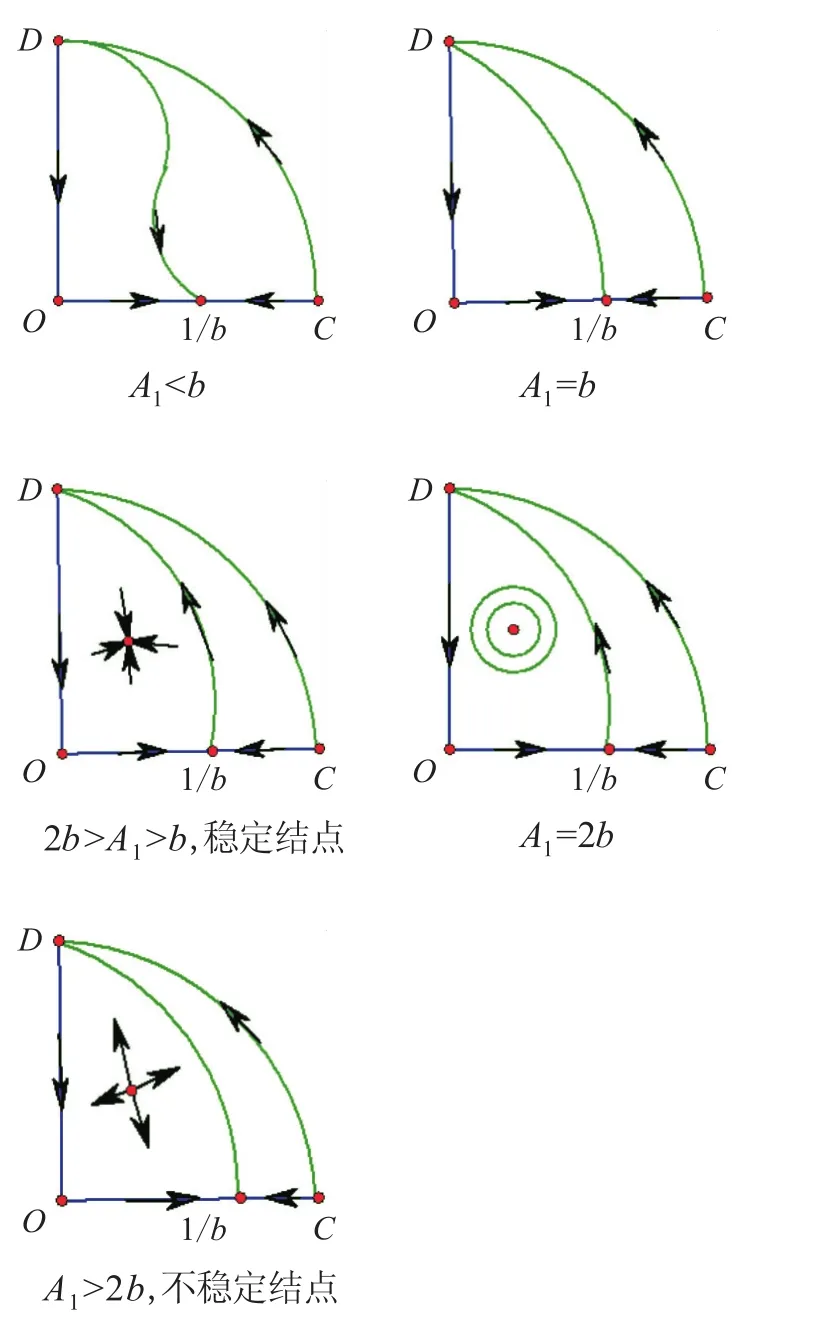
图1 系统(2)的全局结构
5 结束语
本文对文[1]中的功能反应的食饵-捕食者系统重新进行了分析,构造了Dulac函数,利用Bendixson-Dulac定理,给出了系统极限环不存在性的结论,纠正了文[1]中关于极限环存在定理。得出了较为有意义的结果。
[1]程容福,蔡淑文.一类具功能反应的食饵-捕食者两种群模型的定性分析[J].生物数学学报,2002,17(4):406-410.
[2]陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1988:174-198.
[3]张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985:106-110.
[4]张锦炎,冯贝叶.常微分方程几何理论与分支问题[M].北京:北京大学出版社,2000:194-197.
[5]岳宗敏,胡志兴.一类具功能反应的食饵-捕食者两种群模型的极限环的唯一性[J].生物数学学报,2005,20(2):169-172.
[6]吴承强.一类具功能反应的捕食-食饵系统的极限环[J].福州大学学报(自然科学版),2004,32(4):410-412.
[7]颜向平,张存华.一类具功能反应的食饵-捕食者两种群模型的定性分析[J].生物数学学报,2004,19(3):323-327.
A note on the paper“A qualitative of a kind of food with functional response-two group types of predators”
WEI Chang-cheng1,LIN Ji2
(1.School of Mathematics and Computer Science,Tongling University,Tongling Anhui244000,China;2.School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037,China)
In this paper,we consider the kind of food with functional response two-group types of predators again,which has already been studied by article“A qualitative analysis of a food with functional response-two group types of predators”.By structuring Dulac function and using Bendixson-Dulac theorem,we give nonexistence of limit cycles on system(1)and correct the existence of limit cycle of(1).Moreover,we analyze the topological structure of the system(2)in first quadrant.
predator-prey system;Dulac function;limit cycle;topology structure
O175
A
1004-4329(2017)03-018-05
10.14096/j.cnki.cn34-1069/n/1004-4329(2017)03-018-05
2017-05-05
2017年度高校优秀青年人才支持计划项目(gxyq2017081);安徽省质量工程项目(2015jyxm225)资助。
魏长城(1984- ),男,硕士,讲师,研究方向:微分方程稳定性。