几类特殊曲面曲线的法曲率测地曲率和测地挠率的计算

黄 瑞

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

几类特殊曲面曲线的法曲率测地曲率和测地挠率的计算

黄 瑞

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

特殊曲面曲线是曲面论中的一个重要研究对象，坐标曲线、渐近曲线、曲率线和测地线是曲面上常见的几类特殊曲面曲线，而法曲率、测地曲率和测地挠率又是曲面曲线的三个重要的数字特征。本文首先推导出法曲率、测地曲率和测地挠率的性质；其次，列举了三者之间最常见的几种关系；最后，给出上述几类特殊曲面曲线的法曲率、测地曲率和测地挠率的计算公式。

曲面曲线；法曲率；测地曲率；测地挠率

对曲面曲线的研究是经典微分几何中曲面论中非常重要的一部分内容，而特殊的曲面曲线，如坐标曲线、渐近曲线、曲率线和测地线又是我们研究的重中之重，研究内容主要包括它们的曲率、挠率、法曲率、测地曲率、测地挠率等。曲面曲线的测地曲率在曲面的保长对应下是保持不变的，它属于曲面的内蕴几何学研究的内容，其计算公式的推导有许多不同的方法，[1]利用曲面论基本方程进行推导，[2]给出了直接的推导方法，但过程复杂且计算量大，[3-5]给出了曲面在正交坐标曲线网下计算测地曲率的Liouville公式的证明方法。本文列举了法曲率、测地曲率和测地挠率之间最常见的三种关系，并由此得到曲面上的直线、渐近曲线、曲率线和测地线的法曲率、测地曲率、测地挠率的计算公式，而坐标曲线的法曲率、测地曲率、测地挠率的计算公式则由定义推导出来。

1 法曲率、测地曲率和测地挠率的计算与性质

1.1 法曲率

证明 由欧拉公式（1），（2）显然成立，下证（3）。

若P为脐点，则，结论成立。

下设P为非脐点，若为主方向，则结论成立。现设不是P点处的主方向，由（1）不妨假设落在以P为坐标原点，（第一主方向），（第二主方向）为坐标轴的平面直角坐标系的第一象限和第四象限，若记，则，由欧拉公式得

注：在P点的切平面上，以P为坐标原点，（第一主方向），（第二主方向）为坐标轴建立平面直角坐标系，关于对称指的是所在的直线关于对称。

1.2 测地曲率

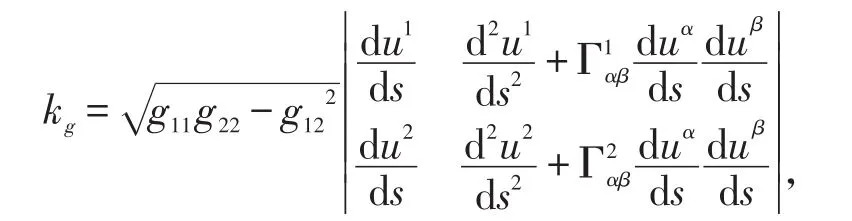
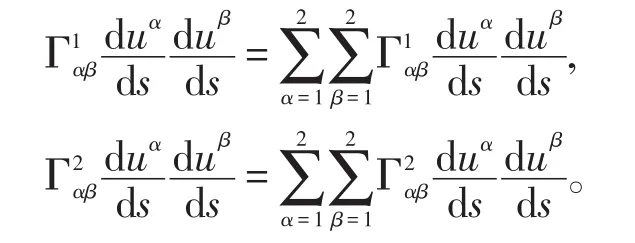
1.3 测地挠率

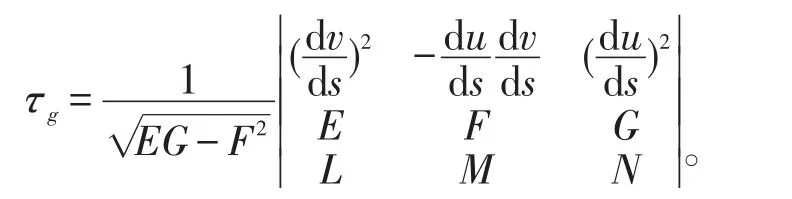
由测地挠率的计算公式知脐点处沿着任意方向的测地挠率都为0，非脐点处沿着主方向的测地挠率为0，即是曲率线的测地挠率恒为0。测地挠率具有类似法曲率的性质。

此定理的证明将在定理5之后给出。

定理3[6]若(c)为曲面上非直线的渐近曲线或测地线，则(c)的挠率等于它的测地挠率。

1.4 法曲率、测地曲率和测地挠率之间的关系

定理4[3]kn2+kg2=k2。

由定理4易见若曲面上存在直线，则直线的法曲率和测地曲率都为0。

特别指出的是，定理5中的θ具有方向性，即从到逆时针转θ为正角，顺时针转θ为负角，而欧拉公式中出现的是sin2θ和cos2θ，因此无需考虑θ的方向性。

证明 若P为脐点，结论显然成立。

在非脐点P的小邻域U内取正交的曲率线网作为参数曲线网，记作(u,v)，且不妨设P点沿u-曲线的切方向为第一主方向，则在P处有，从而

在上述特殊的参数系下，定理5中的θ与Liouville公式中的θ是一致的，根据[3]中Liouville公式的证明过程知

接下来给出定理2的证明。

证明 由定理5知定理2中的（1），（2）显然成立，下证（3）。

若P为脐点，则，结论成立。

下设P为非脐点，若为主方向，则，结论成立。现设不是P点处的主方向，由定理2（1）不妨假设落在以P为坐标原点，（第一主方向），（第二主方向）为坐标轴的平面直角坐标系的第一象限和第四象限，若记从到的角为θ，则从到的角为由定理5,得

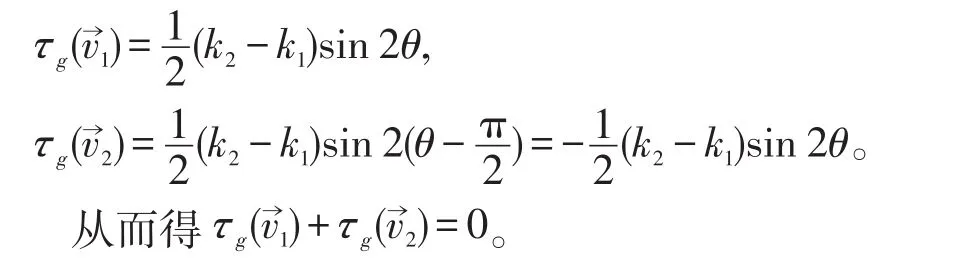
定理6 沿着任意的一条曲面曲线(c)都有成立，其中H,K分别为平均曲率和高斯曲率。

2 特殊曲面曲线的法曲率、测地曲率和测地挠率

2.1 渐近曲线

根据定理3,4，6易得下面的结论。

定理7 设(c)为S上的渐近曲线，若

（1）(c)为直线，则(c)的

（2）(c)不是直线，则(c)的，其中k,τ分别为(c)的曲率和挠率。

由定理7易见可展曲面上的渐近曲线必为平面曲线。

2.2 曲率线

由定理4易得下面的结论。

定理8 设(c)为S上的曲率线，则(c)的法曲率为主曲率，不妨记作，其中k为(c)的曲率。

2.3 测地线

根据定理3,4,6易得下面的结论。

定理9 设(c)为S上的测地线，若

（1）(c)为直线，则(c)的

（2）(c)不是直线，则(c)的kn=±k,kg=0,τg=τ，其中k,τ分别为(c)的曲率和挠率。

由定理9可得曲面上直线的测地挠率未必为零，但平面上的直线以及可展曲面上的直母线都有τg=0，另外若曲面上的测地线为非直线的平面曲线，如球面上的大圆，旋转曲面上的经线等等，则此测地线的测地挠率为0。

2.4 坐标曲线

证明u-曲线(c)的方程还可以写作，由于，从而得到

下求(c)的测地曲率，将测地曲率计算公式中的张量记号转换成高斯记号得到(c)的测地曲率

从而得到(c)的测地曲率

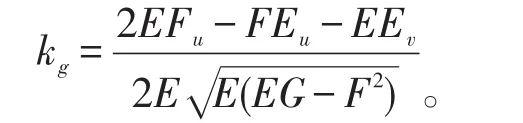
同理可得到下面的定理。

3 结束语

本文首先给出了法曲率、测地曲率和测地挠率的一些“有趣”的性质，如沿着两个共线的切方向，法曲率和测地挠率都相等，而沿着两个正交的切方向，法曲率之和为该点处的主曲率之和，测地挠率之和为零。其次总结了法曲率、测地曲率和测地挠率之间的关系，并由此轻松得到直线、渐近曲线、曲率线和测地线这4类特殊曲面曲线的法曲率、测地曲率和测地挠率的计算公式。最后用最原始的定义法得到任意曲面的坐标曲线的法曲率、测地曲率和测地挠率的计算公式，特别地Liouville公式是本文定理10,11中测地曲率计算公式的特例。

[1]梅向明，黄敬之.微分几何[M].4版.北京：高等教育出版社，2008：146-149.

[2]邢家省，张光照.曲面上曲线的测地曲率向量的注记[J].吉首大学学报(自然科学版)，2013，34（4）：7-10,15.

[3]陈维桓.微分几何[M].北京：北京大学出版社，2006：229-237.

[4]邢家省，白 璐，高建全.曲面正交网下测地曲率计算公式的推导方法[J].四川理工学院学报(自然科学版)，2015，28（4）：75-79.

[5]罗秀华，张光照，邢家省.曲面正交网下测地曲率和高斯曲率的计算公式的推导方法[J].河南科学，2015，33（7）：1081-1086.

[6]黄 瑞.特殊曲面曲线的性质[J].阜阳师范学院学报(自然科学版)，2016，33（3）：8-11.

Calculations of normal curvature,geodesic curvature and geodesic torsion of some special types of curves on surface

HUANG Rui
(School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037，China)

Special curve on surface is an important research object in surface theory.Coordinate curves,asymptotic line,curvature line and geodesic line are some special curves which are common on surface,while normal curvature,geodesic curvature and geodesic torsion are the three important numerical traits.This paper first derives the nature of normal curvature,geodesic curvature and geodesic torsion,then lists some common relations among the three,and lastly provides the calculation formulas of normal curvature,geodesic curvature and geodesic torsion of the special types of normal curvature.

curve on surface;normal curvature;geodesic curvature;geodesic torsion

O186.1

A

1004-4329（2017）03-023-04

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）03-023-04

2017-06-17

安徽省高校自然科学研究重点项目（KJ2017A341）；安徽省质量工程项目（2014zy138，2015gxk149）；阜阳师范学院质量工程项目（2016JYXM23，2016JYXM25）资助。

黄 瑞(1985- )，女，硕士，讲师，研究方向：微分几何。