半正定分块矩阵的几个奇异值不等式
刘俊同
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
半正定分块矩阵的几个奇异值不等式
刘俊同
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
本文应用Hermitian矩阵的性质、矩阵的分块技巧以及矩阵的优超技术,证明了半正定分块矩阵的几个奇异值不等式。
半正定矩阵;优超;奇异值不等式
奇异值不等式和奇异值分解是矩阵理论的一个重要研究领域,在科学计算、优化问题、最佳逼近等实际应用中都有着重要应用。关于矩阵酉不变范数不等式和奇异值不等式问题是矩阵不等式的研究热点之一,近年来受到国内外专家学者的广泛关注[1-4]。文献[5]研究了矩阵的算术平均-几何平均以及奇异值不等式;文献[6-9]讨论了一些特殊条件下矩阵的奇异值不等式。本文应用Hermitian矩阵的性质、矩阵的分块技巧以及优超技术,获得了半正定分块矩阵的几个奇异值不等式。
1 预备知识
为了叙述方便,对符号作如下约定:R表示实数域,Mm,n(或Mn,若m=n)表示复数域上全体n×n矩阵,A∗表示矩阵A的共轭转置矩阵,A⊕B表示分块对角矩阵。对于Hermitian矩阵A∈Mn,用λi(A),i=1,2,…,n,表示矩阵A的非增有序特征值,σi(A),i=1,2,…,n,表示矩阵A的非增有序奇异值,也就是矩阵的特征值。λ(A)和σ(A)分别表示矩阵A的特征值和奇异值向量,即
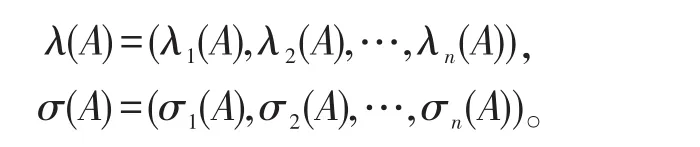
给定两个Hermitian矩阵A,B∈Mn,偏序A≥B按通常意义表示矩阵A-B是半正定的,相应的,A>B表示矩阵A-B是正定的。给定两个向量x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn,设表示向量x的坐标按非增次序重排后所得向量,若满足


则称向量x被y弱对数优超,记作x≺wlogy。进一步地,称向量x被y对数优超,记作x≺logy,当k=n时,等式成立,请参见[1]。
2 引理
引理1[3]给定两个Hermitian矩阵A,B∈Mn,则有

引理2[10]给定两个Hermitian矩阵A,B∈Mn,则有
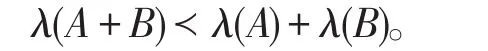
引理3[10]给定两个Hermitian矩阵A,B∈Mn,则有

引理4[8]给定半正定分块矩阵,其中A∈Mm,C∈Mn,r=min{m,n},则有
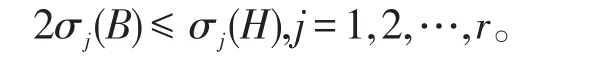
引理5[1]给定分块矩阵,其中B∈Mm,n,若σ1(B),σ2(B),…,σr(B)为矩阵H的非零奇异值,其中r=min{m,n},则有

为矩阵B的非增有序特征值。
在当今国有企业的竞争中,人力资源部门的任务不仅仅是为企业招贤纳士,在对企业内部的人员管理上,也承担着重要任务。在国有林场中,员工素质的高低直接影响林场目标和价值的实现,人力资源通过激励和考核体系,提高员工的积极性,对员工的工作进行评价,能够激发员工热情,有利于完成企业目标。三门江林场规模较大,各个岗位员工较多,难以管理。通过制定合理有效的员工绩效考核和人才选拔考核制度,可以让人力资源管理工作井井有条,为林场的员工提供良好的培养系统。
3 主要结果

对j=1,2,…,r,成立。
证明 因为
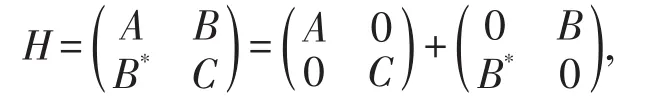
由引理1,有
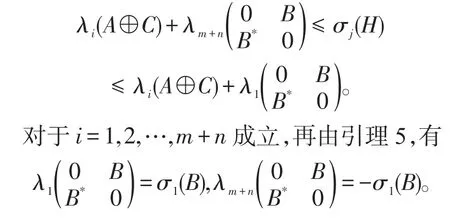
所以

对j=1,2,…,r,都成立。

对于k=1,2,…,n都成立。
证明 由引理2和引理5,有
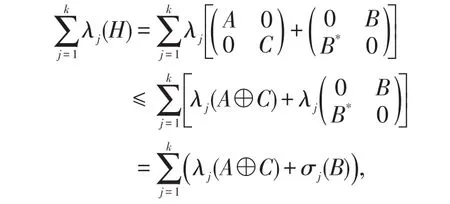
对于k=1,2,…,n都成立。又因为
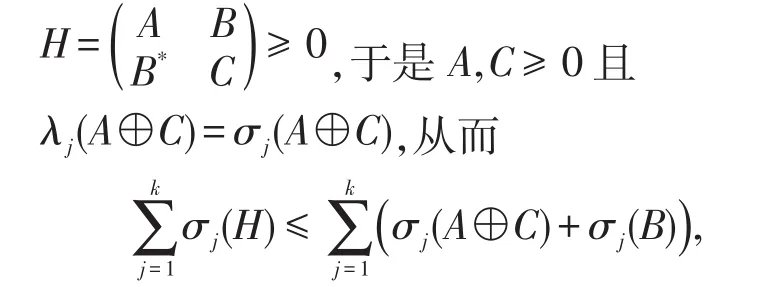
对于k=1,2,…,n都成立。另一方面,因为
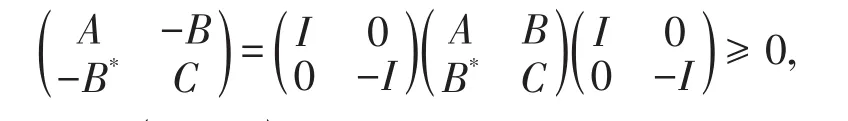

对于k=1,2,…,n都成立。所以,有
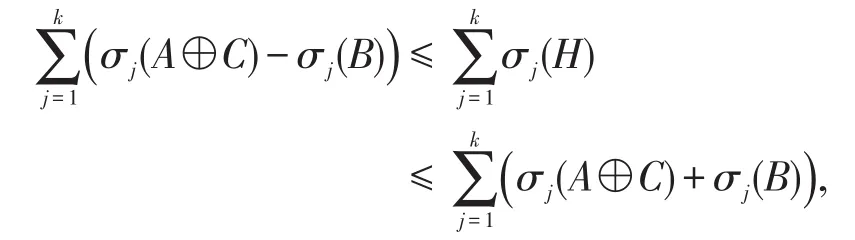
对于k=1,2,…,n都成立。
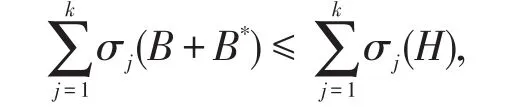
对于k=1,2,…,n都成立。

由引理2,有

再由引理4,有
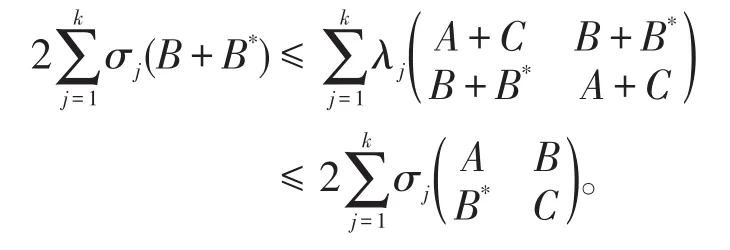
即

对于k=1,2,…,n都成立。
[1]Horn R A,Johnson C R.Matrix analysis[M].Cambridge:Cambridge university press,2013:279-372.
[2]Horn R A,Johnson C R.Topics in matrix analysis[M].Cambridge:Cambridge university press,1991:134-238.
[3]Zhan X.Matrix inequalities[M].Berlin:Spinger-Verlag,2002:17-25.
[4]王松桂,吴密霞,贾忠珍.矩阵不等式[M].北京:科学出版社,2006:222-288.
[5]Zou L.A arithmetic-geometric mean inequality for singular values and its applications[J].Linear Algebra andApplications,2017,528:25-32.
[6]邹黎敏.矩阵的几个不等式[J].数学通报,2012,55(4):715-720.
[7]宫 琴,任芳国.关于矩阵奇异值的不等式[J].纺织高校基础科学学报,2016,29(1):1-7.
[8]Tao Y.More results on singular value inequalities of matrices[J].Linear Algebra and Applications,2006,416(2):724-729.
[9]Zhang F.Matrix inequalities by means of block matrices[J].Mathematical Inequalities and Applications,2001,4(4):481-490.
[10]Zhang F.Matrix theory:basic results and techniques[M],second edition,Springer,2011:102-123.
Inequalities with singular values of positive semidefinite block matrices
LIU Jun-tong
(School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037,China)
In this paper,based on the properties of Hermitian matrix,the techniques of block matrices and the majorization theory,some inequalities for singular values of positive semi-definite block matrices are obtained
positive semidefinite matrix;majorization;singular value inequality
O151.21
A
1004-4329(2017)03-027-03
10.14096/j.cnki.cn34-1069/n/1004-4329(2017)03-027-03
2017-06-19
安徽省教学研究项目(2015jyxm225,2016jyxm0754);阜阳师范学院科研项目(2016FSKJ20)资助。
刘俊同(1982- ),男,博士生,讲师,研究方向:矩阵不等式、矩阵方程以及算子理论。