归纳法在高中数学解题中的运用

蒋正洋

(江苏省扬州市树人中学高二(二)班,江苏 扬州 225000)

归纳法在高中数学解题中的运用

蒋正洋

(江苏省扬州市树人中学高二(二)班,江苏 扬州 225000)

在高中数学解题当中，归纳法是其中常用的解题方法之一，尤其是针对一类问题以及规律问题的解答当中，更是重要的解题途径.该类解题方法要求高中学生在日常学习的过程中，首先对例题深入分析，之后对解题思路进行归纳、总结，以便在今后的解题当中能够熟练使用.

高中数学；归纳法；等式问题；不等式问题；高中几何

一、归纳法在高中等式问题当中的运用

对于高中学生而言，其在知识的学习、理解以及运用方面均存在一定程度的差异，因此其在解题思维方面也将会不尽相同.在面对高中数学问题时，部分高中学生由于数学思维的欠缺，导致其在审题的过程中，常常会因漏掉已知条件而使得问题无法解决.在现今的高中数学知识学习当中，部分已知条件并不会在题目当中直接给出，而是隐含在给定的条件之内.当高中学生没有将知识融会贯通时，则有可能出现问题.在高中数学当中，等式问题是常见的问题之一，也是运用归纳法进行解决的典型问题之一.

“牛吃草”问题是高中学生解题的过程中常遇到的难题之一，其主要难点在于牛在吃草的同时，草也在不断的生长.消耗量与生长量之间的关系，是讨论该类问题的关键所在.例如，设y是一片草原当中草的生长总量，N表示在该片草地当中放牧的牛的总数，x表示草地在自然状态下的生长速度，T是牛吃草的总时间，则可得出y=(N-X)T这样的公式.类似的问题如在一片河流当中，其河道当中沉积着一定量的砂子.当80个人昼夜不断的开采砂子时，可开采180天；当60个人昼夜不断的开采砂子时，可开采300天.如若保证河道中的砂子不被开挖枯竭，则可有多少人昼夜不断的开挖？在对该类问题进行解答时，可将每个人的开挖速度设为X，则可以根据砂子的总量不变这一原则，得出(80-X)×180=(60-x)×300，最终得出X=30.

二、归纳法在高中不等式问题当中的运用

不等式的高中数学当中常见的问题之一，也是高中学生学习、解题的难点所在.因此，高中学生在数学知识的学习时，应首先根据自身的实际特点，寻找适合自身的数学知识学习方法，并以此方法为基础，提高对数学新知识的学习程度，将知识融入到自己的数学体系当中，对知识当中的内在联系进行发现、总结.对于简单的一元高次不等式而言，其主要的解题方法为区间法(或称根轴法)，其具体解题步骤包括以下几个：其一，去掉f(x)的最高次项的系数的负号；其二，将f(x)因式分解；其三，设每个括号的因式为0，将解标注到数轴之上；其四，根据题目要求，写出不等式的解集.而在对分式不等式进行解题的过程中，应将已知问题整理成 “>0”或 “≥0”的形式，转化为整式不等式求解，

例如，用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·2…(2n-1) (n∈N)，从“k到k+1”，左端需乘的代数式为____.

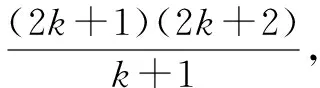
A.2k-1B.2k-1 C.2kD.2k+1在对该类问题进行解答时，应将原式转化为(2k+1-1)-(2k-1)=2k，因此其正确答案应选C.

三、归纳法在高中几何问题当中的运用

所谓的归纳推理，其实质以现有的事物为基础，对其中包含的规律进行总结，进而在遇到其他类似的问题时，可将该类规律运用到新问题的解答当中.而归纳推理的步骤主要包括以下几个：其一，对现有的事物进行仔细的研究；其二，根据现有的事物总结出具有一般性的规律.在高中数学几何问题学习的过程中，类比推理也是常用的方法之一，其实质根据两类不同事物之间具有某些类似性，推出其中一类事物具有另一类事物类似的性质的推理，其主要步骤包括：其一，对不同的已知问题进行研究，找出其中相同或者相似之处；其二，根据相似之处总结规律，运用到其他问题的解答当中.在几何问题当中运用归纳法时，其所解决的问题主要包括几何问题中各个量的计算以及几何问题的证明.然而，归纳法的运用并不意味着以往解题思路、数学知识的几点套用，而是应根据新、旧知识对问题进行揣摩，并做好知识的迁移.

例如，有n个圆，相邻的两个圆之间均有交点，并且每三个圆都不相交于同一点，求证：这n个圆把平面分成f(n)=n2-n+2个部分.

证明：①当n=1时，即一个圆把平面分成二个部分f(1)=2；又n=1时，n2-n+2=2，∴命题成立.

②假设n=k时，命题成立，即k个圆把平面分成f(k)=k2-k+2个部分，那么设第k+1个圆记⊙O，由题意，它与k个圆中每个圆交于两点，于是它与其它k个圆相交于2k个点.把⊙O分成2k条弧而每条弧把原区域分成2块，因此这平面的总区域增加2k块，即f(k+1)=k2-k+2+2k=(k+1)2-(k+1)+2即n=k+1时命题成立.由①②可知对任何n∈N命题均成立.

在高中数学知识的学习过程中，学生只有根据已经掌握的数学知识以及典型的例题，对其进行深入的研究分析，明确解题思路，总结解题方法，归纳出一套行之有效的学习方法，进而能够提升数学的学习效果.

[1]邹毅,杨发建.运用归纳法和演绎法施教的比较研究[J].江西教育科研，2004(11).

[2]余昌木.数学归纳法应用举例[J].高中生之友，2005(21).

G632

A

1008-0333(2017)22-0043-02

2017-06-01

蒋正洋(2000.10.16-),江苏省兴化,在校学生.

责任编辑：杨惠民]