几何法巧解向量题

黎金传

(浙江省镇海中学，浙江 宁波 315200)

几何法巧解向量题

黎金传

(浙江省镇海中学，浙江 宁波 315200)

平面向量是高考中命题的重点与热点.用几何法的优势在于直观形象，计算量小，解题速度快.关键是:根据题意找出其几何意义，再结合题意画出几何图形，这样就在直观图形中，找到要求的几何意义，从而找到解题思路，有效减少计算量，达到事半功倍的效果.

平面向量；几何法；几何意义；几何图形

平面向量具有代数与几何双重身份， 是沟通代数与几何的桥梁,堪称数与形的完美结合.它是中学数学知识网络重要的交汇点， 也是高考中命题的重点与热点.平面向量本身具有几何的特性，它的加、减、数乘及数量积的运算均具有几何意义.因此在处理平面向量问题时，可考虑平面向量的几何意义，将它与平面几何及解析几何联系起来. 用几何法的优势在于直观形象，计算量小，解题速度快.

例1 已知向量a≠e,|e|=1,满足对任意t∈R，恒有|a-te|≥|a-e|，则

A.a⊥eB.a⊥(a-e)

C.e⊥(a-e) D.(a+e)⊥(a-e)

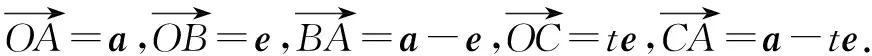
例2 若平面向量a,b满足|2a-b|≤3，则a·b的最小值为________.

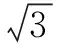
例4 已知非零向量a,b,c满足|a-b|=1，(a-c)·(b-c)=0，设|c|的最大值与最小值分别为m,n，则m-n的值为____.

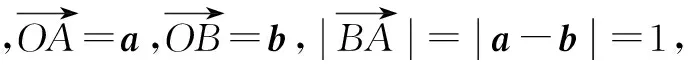
例5 已知向量a,b满足|a|=|b|=a·b=2，且(a-c)·(b-2c)=0，则|b-c|的最小值为____.

A．(0,1) B．(1,2]

C．(-1,0) D．[-2,-1)

注：选择题可以用特例法，锐角三角形ABC为等边三角形时x=y=-1,x+y=-2,选D.

通过这些例题我们发现用几何法解向量题关键是:根据题意找出其几何意义，再结合题意画出几何图形，这样就在直观图形中，找到要求的几何意义，从而找到解题思路，有效减少计算量，达到事半功倍的效果.

[1]G.波利亚. 怎样解题[M].徐泓，冯承天译.上海:上海科技教育出版社，2007.

[2]罗增儒.中学数学解题的理论与实践[M].南宁：广西教育出版社，2008.

G632

A

1008-0333(2017)22-0018-02

黎金传，男,中小学正高级教师，特级教师.

责任编辑：杨惠民]