探究一道高考三角形面积最值试题的解法

刘 刚 赵 毅

(北京市第十二中学高中部，北京 100071)

探究一道高考三角形面积最值试题的解法

刘 刚 赵 毅

(北京市第十二中学高中部，北京 100071)

2013年高考福建数学文科第21题考查了一道以等腰直角三角形为背景，求内接三角形面积最值问题．试题既要立足图形，分析图形特征，又要借助代数运算求解，是一道典型的数形结合的题目．试题解法灵活，使不同学生有了更多的选择，体现了新课标理念．

高考;等腰直角三角形;面积最值

课题项目：本文系北京市丰台区“十三五”重点课题《新课程背景下高中数学竞赛教学研究》(课题批准号：2016237-J)阶段成果之一．

一、试题

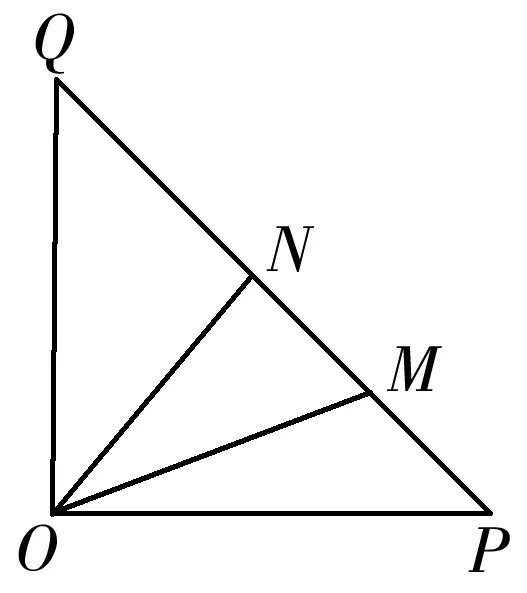
图1

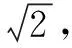
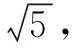
(Ⅱ)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,ΔOMN的面积最小?并求出面积的最小值.

二、解法探究

(Ⅰ)略．(Ⅱ) 设∠POM=α,则0°≤α≤60°．具体解法如下：

分析1 在△OMP与△ONQ中分别利用正弦定理表示出OM,ON，然后借助两边及夹角的三角形面积公式表示出三角形的面积，运用两角和公式及二倍角公式进行三角恒等变换，最后分析三角函数的性质求得最值．

解法1直接表示△OMN的面积

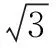
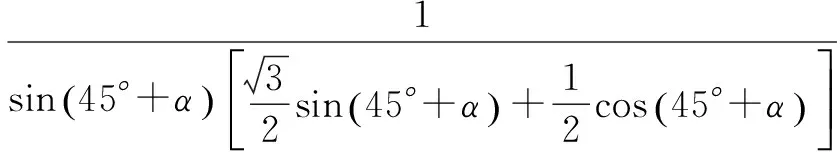
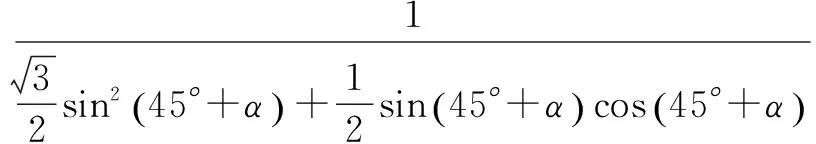
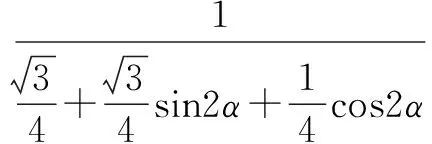
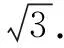
分析2 由于MN在等腰直角△POQ的斜边PQ上运动，所以过点O作PQ的垂线段OR构造直角△RON、△ROM，利用锐角三角函数分别表示RN，RM，在此基础上就可以表示出MN，然后借助基本不等式进行求解，解题过程体现了分类与整合、数形结合的思想方法．

解法2化斜为直表示MN

过点O作OR⊥PQ于点R，则点R是PQ的中点，OR=2，设∠ROM=β．

图2

(ⅰ)如图2，当点M,N在点R两侧时， 则0°<β<30°，所以∠NOR=30°-β．在Rt△RON中，NR=2tan(30°-β)，在Rt△ROM中，MR=2tanβ，所以

MN=2[tan(300-β)+tanβ]

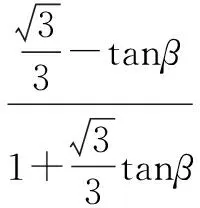
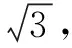
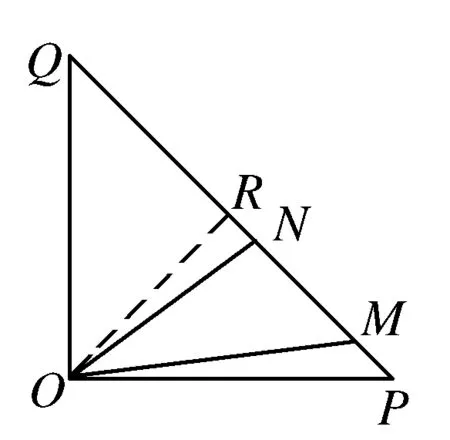
图3

分析3 在△OMN中先利用面积表示出两边OM,ON之间的关系，然后利用余弦定理表示出MN，最后借助均值不等式进行求解．

解法3均值不等式法

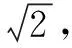
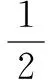
分析4 本题是一道动态中的三角形面积最值问题，有不少学生都能直观猜出当∠POM=30°时△OMN的面积最小，但是为什么最小，一些学生并没有进行证明，造成了不必要的失分，当然跟不会证有关．实际上以∠POM=30°时的△OMN为基准，证明在其它位置时三角形的面积都大，即MN都长即可，证明过程中要结合正弦定理以及三角形性质进行说明．大胆猜想，小心求证是解决动态问题的常用方法．

解法4先猜后证法

猜想α=30°时，△OMN的面积有最小．如图4，设α=30°时的△OMN记为△OM′N′，此时OM′=ON′．

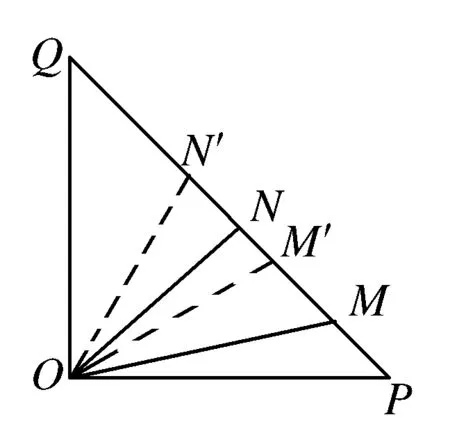
图4

(ⅰ)当0°<α<30°时，设∠MOM′=β，则∠NON′=β．

(ⅱ)同理可得当30°<α<60°时，MN>M′N′．

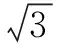
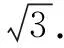
[1]刘刚，赵毅．一道高考三角形试题的多解与多变 [J]．中学数学杂志，2016，5．

[2]刘刚 赵毅．一道习题的求解与拓展[J]．数理天地(高中版)，2016，9．

[3]刘刚．对一道竞赛三角试题的探究与变式 [J]．数学通讯(上半月)，2017，5.

G632

A

1008-0333(2017)22-0025-02

刘刚(1975.4-)，男，大学本科，中学高级教师，从事数学教育.赵毅(1977.5-)，女，大学本科，中学高级教师,从事数学教育.

责任编辑：杨惠民]