构造思想在数学分析中的应用

张利红

(天津师范大学数学科学学院，天津 300387)

构造思想在数学分析中的应用

张利红

(天津师范大学数学科学学院，天津 300387)

本文主要介绍了构造思想方法的含义及构造思想在数学分析中的作用：如通过构造实例来论证某些判断或命题成立与否;通过构造恰当函数,应用根的存在定理证明与中间值有关的等式,应用函数单调性证明不等式;构造特殊区域上的函数来证明一般区域上的函数具有的相关性质;在积分学中通过构造对称性来简化积分问题的计算.以上构造思想在数学分析当中的应用加深了我对数学分析理论的理解,也认识到这种思想的重要性.

构造反例;构造函数;构造区域;构造对称

一、构造思想方法

1.构造思想方法的概念

构造思想方法是通过“构造”来建立数学理论,根据题设条件或结论所具有的特征、性质,构造出满足条件和结论的数学模型,借助此模型解决数学问题的重要数学思想方法之一.

2.运用构造思想方法的条件

在学习数学分析这门课程中,当有的结论难以直接表达时,需要借助一定的条件才能转化到结论,于是就可以利用数学问题的特殊性,进行新的关系结构的设计.这种方法不是直接解决问题,而是构造一个与原来问题有关或等价的新问题间接地解决.

二、构造反例的思想在数学分析中的应用

1.构造反例的作用

在数学分析中,命题判断的题目很多,从理论上去直接证明命题是否正确,往往难以找到突破口,若能构造一个反例,说明命题不成立,问题便得到解决.构造反例的过程,是使我们对数学分析理论理解逐步加深的过程,使我们的数学能力逐步提高的过程.

2.构造反例的应用举例

例1 判断正误:无界数列与无界数列的积仍为无界数列.

三、构造函数

1.在数学分析中构造函数的作用

在数学分析中构造出有利解决问题的辅助函数,往往能使很多复杂问题难度降低,利用辅助函数的性质和定理进行求解,开拓了思维,进而在解题或问题证明中取得事半功倍的效果.构造辅助函数的思想是数学分析中重要数学思想之一.

2.构造函数的应用举例

(1)构造函数应用根的存在定理证明等式

这种方法的关键是如何根据已知条件和结论的特点构造符合根的存在定理的函数,从而应用根的存在定理.应该利用三步法：(1)结论移向变形;(2)换变量;(3)构造新函数.

例2 设函数f(x)在[0,2a]上连续,且f(0)=f(2a).证明:存在点x0∈[0,a],使得f(x0)=f(x0+a).

证明令F(x)=f(x)-f(x+a),由于f(x)在[0,2a]上连续,所以f(x+a)在[0,a]上连续,所以F(x)在[0,a]上连续.又F(0)=f(0)-f(a),F(a)=f(a)-f(2a)=f(a)-f(0),若f(0)=f(a),则取x0=0,a;若f(0)≠f(a),则F(0)=-F(a),

∴F(0)·F(a)<0.

由根的存在定理,存在x0∈(0,a),使得F(x0)=0,即f(x0)=f(x0+a).

综上,存在点x0∈[0,a],使得f(x0)=f(x0+a).

(2)构造函数证明积分不等式问题

在一些既有积分也有函数的不等式证明题中,由于成分复杂,直接计算或是找他们之间的联系是很困难的,往往通过构造函数,把不等号两边看是无关的式子联系起来,使得问题得到巧妙地解决.证明不等式的一般思路(三步法):

(1)移向变形;

(2)换变量;

(3)构造函数.

然后再根据函数的单调性证明不等式.

F(a)=0.

F′(x)=M(x-a)±f(x)=M(x-a)±[f(x)-f(a)]

=M(x-a)±f′(ξ)(x-a)=[M±f′(ξ)](x-a),

其中ξ∈(a,x).

又∵|f′(x)|≤M,

∴F′(x)≥0,∴F(x)在[a,b]上单调递增.

又F(a)=0,

∴∀x∈[a,b],F(x)≥0.

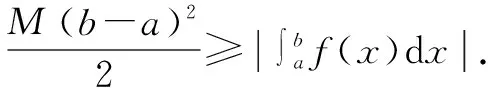
(3)延拓函数定义域构造函数使复杂问题得以简化

分析由函数的一条性质:若函数f(x)在[a,b]上连续,则f(x)在[a,b]上一致连续.可以将证明f(x)在(a,b)上一致连续转化为f(x)在[a,b]上连续.

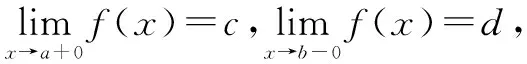
则F(x)在[a,b]上连续,从而在[a,b]上一致连续,∴f(x)在(a,b)上一致连续.

四、构造对称

1.构造对称的作用

构造对称,就是要添加一些不与题设矛盾的条件,使之具有对称性，充分利用对称性解决问题.该方法在数学分析微积分中经常使用,掌握好它,有时能避开很多繁琐的计算.比如构造对称形式的积分建立方程组求解就是常见的应用,充分体现了构造对称计算积分的优势.

2.构造对称的应用举例

在数学分析中,构造思想是一种极其重要的解题思想.运用构造思想方法解题时,要对题目全面分析,从中发现可用构造的因素,并借助与之相关的知识构造所求问题的具体形式,或是与其等价的新问题,再解出所构造的问题,从而使原题目获得解答.就构造的对象而言,其表现形式多样,没有完全固定的模式.除了以上介绍的方法外,还有构造三角模型、构造集合等方法.因此,运用构造思想方法解题,需要掌握牢固的基础知识,熟练的技能技巧,而且还应具有发散思维能力,综合运用各方面知识的能力.构造思想法没有很固定的模式,它很灵活,不死板.因此,这种解题方法的操控空间性及思维创造性较大.当然文中介绍的方法毕竟有限,笔者只是从个人方面谈了自己对构造思想的认识及理解,敬请各位读者批评指正.

[1]刘良华.数学构造思想方法的探索与实践[D].华中师范大学,2004.

[2]丁文敏.构造法的数学思想及其运用[J].南阳农业职业学院学报,2014.

[3]李志飞.罗尔定理应用中辅助函数的构造[J].西安建筑科技大学理学院学报,2006.

G632

A

1008-0333(2017)22-0008-02

2017-06-01

张利红(1991.8-),女,汉族,河北张家口人,研究生在读,助教,从事科学技术史.

责任编辑：杨惠民]