齿轮轴向重合度对传动误差的影响

赵腊月， 杜明刚， 杨 阳， 边骥轩

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

齿轮轴向重合度对传动误差的影响

赵腊月， 杜明刚， 杨 阳， 边骥轩

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

采用一种经试验验证过的3D 轮齿接触分析(TCA)方法，研究1对直齿轮和7对斜齿轮在同等载荷强度下，轴向重合度对传动误差的影响.为保证结果更接近实际情况，在计算时考虑由加工误差导致的齿轮啮合错位量和适当的微观修形.结果表明：齿轮轴向重合度为略大于整数的值时，其传动误差最小，如1.02～1.05.

齿轮传动误差；齿轮轴向重合度；啮合错位量；微观修形；3D-TCA方法

Abstract：A pair of spur gears and seven pairs of helical gears were studied to investigate the influence of overlap ratio on transmission error under the same load intensity by using a validated 3D-Tooth Contact Analysis(TCA) method. To ensure the results being closer to the actual situation, mesh misalignment due to manufacturing deviations and appropriate micro modifications will be applied to the gears. The results show that when the overlap ratio is slightly greater than an integer constant, the transmission error is minimum； for example the overlap ratio is equal to 1.02～1.05.

Keywords: Transmission error；overlap ratio；mesh misalignment；micro modifications；3D-TCA method.

齿轮传动由于其高功率密度、高效率和高可靠性的优点，被广泛用于机械、车辆、航海、航空、航天等领域.近几年来，对齿轮传动的要求已经不仅仅限于强度和可靠性，低振动、低消耗和低噪声齿轮传动的研究已经越来越受到重视.齿轮传动误差是公认的齿轮噪声源之一，同时也是降低齿轮振动和噪声的最好的控制参数之一.之前的很多研究已经证明，降低传动误差可以降低齿轮噪声级[1].因此，降低齿轮传动误差已经成为齿轮优化的主要设计参数.

齿轮传动误差的研究已经明显降低了齿轮传动系统的振动和噪声.例如，Yin Jia[2]依据齿轮啮合理论，考虑轮齿变形，分析了不同载荷条件下的静态传动误差，研究了中心距偏差对静态传动误差的影响.Tesfahunegn[3]〗、Velex[4]and Kissling[5]研究了渐开线修形对传动误差的影响.Frazer[6]用一个经过验证的3D有限元分析(FEA)和轮齿接触分析(TCA)程序优化齿轮来降低传动误差.但是，还需要进一步地研究并理解影响齿轮传动误差的关键参数，并且提供实际的参考值.齿轮轴向重合度(εβ)和齿轮啮合接触线长度的变化密切相关，齿轮啮合线长度的变化将会导致齿轮传动误差.然而，目前齿轮轴向重合度对传动误差的影响还没有系统的研究.因此，对这方面的研究是至关重要和有实际意义的.本研究主要分析了齿轮轴向重合度对传动误差的影响，从结果中得出了获得最小传动误差的齿轮轴向重合度的最优推荐值.为保证结果的有效性和实用性，分析中同时考虑由制造误差导致的齿轮啮合错位量和适当的齿轮微观修形[7].

1 齿轮传动误差的计算和齿轮轴向重合度的定义

1.1 齿轮传动误差的定义

齿轮传动误差的定义为：在恒定输入扭矩下，输出齿轮的实际位置与理论位置的差值[8].如图1所示，在恒定载荷下，理论上，从主动轮到被动轮可以传递恒定的转速，但是在实际状态下，轮齿啮合时，由于制造误差、装配误差、轮齿弹性变形等因素的影响，被动轮的实际转动位置总是偏离其理想位置.被动轮转动位置的偏离量转化到接触线上的位移量即为齿轮传动误差(见公式1).

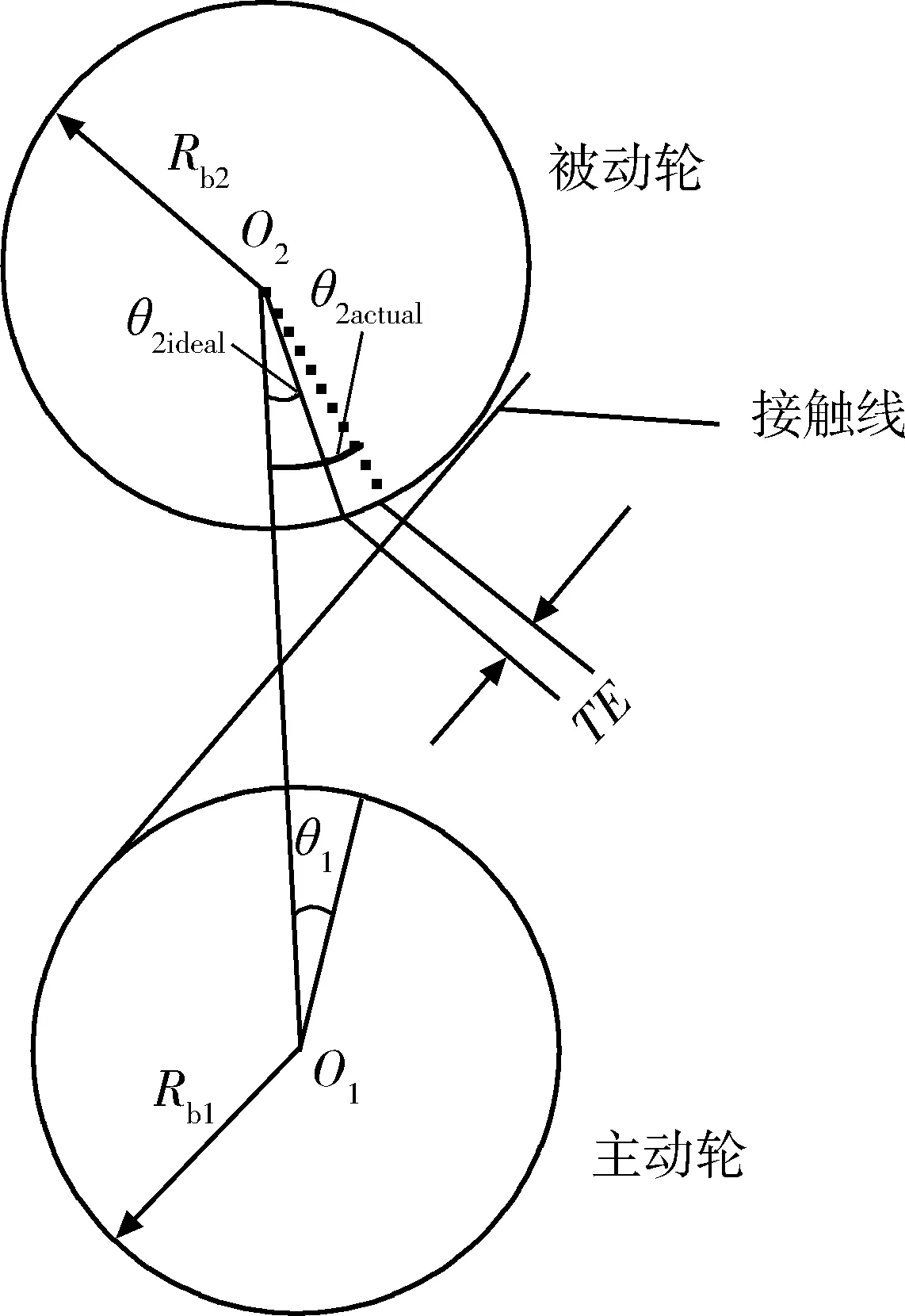
图1 齿轮传动误差的定义

TE=(θ2actual-θ2ideal)Rb2.

(1)

齿轮传递误差使齿轮啮合时的干涉增大，破坏了齿轮传动的平稳性，产生振动和噪声.因此，预测和降低齿轮传动误差是降低齿轮箱振动和噪声的有效途径之一.

1.2 齿轮传动误差的计算

本研究中，采用一个经过试验验证的3D-TCA方法-GATES(Gear Analysis for Transmission Error and Stress)来分析齿轮传动误差.GATES最初是由英国纽卡斯尔大学的Design Unit 开发和试验验证，现在由Dontyne公司[9]收购和继续开发.GATES的主要功能是通过定义齿轮宏观参数和微观参数来优化齿轮性能，并考虑啮合错位量和制造误差来降低齿轮振动.GATES中的齿轮传动误差的准确性是由测量名义运行速度下的动态轴承载荷来验证的.齿轮啮合错位量的准确性是利用应变片测量齿宽方向的载荷分布来验证的[10].

采用GATES计算齿轮传动误差的两个步骤为：

1)定义齿轮宏观参数.通过3D有限元分析建立齿轮刚度矩阵，同时计算中还需设置齿轮安装位置的轴径、扭矩传递路径、输入轴旋转方向(顺时针或逆时针)、主动轮为大齿轮还是小齿轮.

2)齿轮接触分析.包括定义载荷工况、齿形误差、安装误差和详细的微观几何参数，计算接触线长度、传动误差、应力和其它功能参数.

本文中，齿轮的传动误差由GATES计算，同时接触线长度的变化也会被计算.通过计算结果的对比，建立齿轮轴向重合度和传动误差的关系.

1.3 齿轮轴向重合度的定义

很多齿轮参数会影响传动误差，轴向重合度是其中一个决定齿轮传动误差的关键因素.因为轴向重合度和齿轮啮合接触线长度的变化密切相关，齿轮接触线长度的变化会导致传动误差.

齿轮轴向重合度是斜齿轮在轴向方向的轮齿运行重合度，如图2所示.计算公式见式(2).

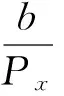
(2)

式中：b为齿宽，mm；Px为轴向节距，mm；β为螺旋角，(°)；mn为法向模数，mm.

图2 齿轮轴向重合度的定义[11]

2 齿轮参数定义

本研究以1对直齿轮和轴向重合度为0.8、0.9、0.98、1.0、1.02、1.1、1.2的7对斜齿轮为研究对象.这8对齿轮的几何参数见表1.这些齿轮参数的选择是为了保持切向渐开线参数的一致性，便于对比.实际中，大多数齿轮设计定义法向平面的齿轮参数，但是，这会导致明显的不同螺旋角齿轮的几何匹配问题，不能保证这些齿轮具有相同的载荷强度(Ft/b).还有一点值得注意的是，选择窄齿宽是为了减小轮齿弹性变形对传动误差的影响.

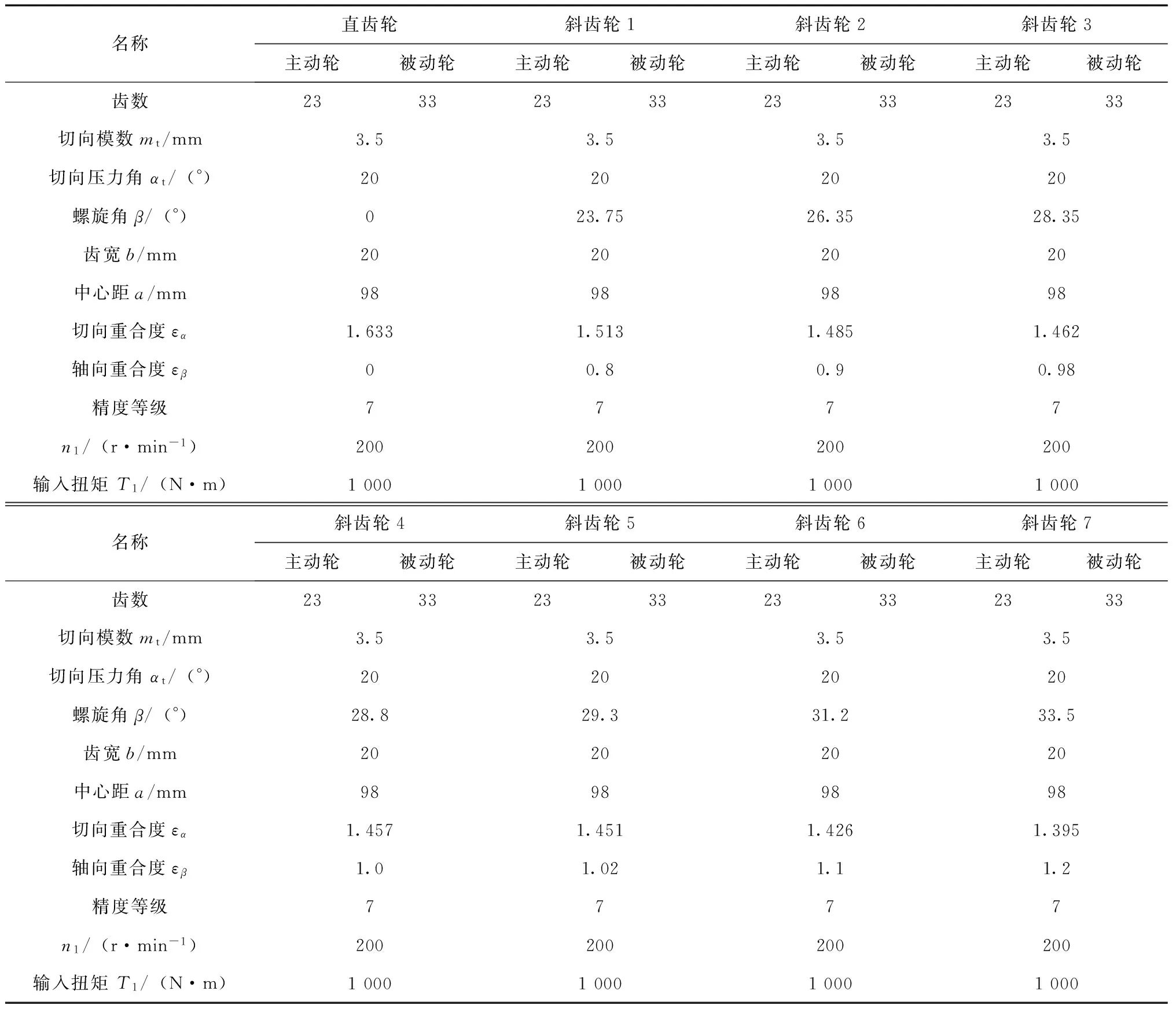
表1 齿轮参数

为了保证分析结果更接近于实际情况，计算时考虑由制造误差导致的齿轮啮合错位量和适当的微观修形.

其中，制造误差导致的齿轮啮合错位量由式(3)[7]计算.

(3)

式中：fHβ1和fHβ2是小齿轮和大齿轮的螺旋角倾斜偏差，与齿轮精度等级相关，具体值可查询ISO 1328[12].

还有一点需要注意的是，齿轮微观修形也会影响其传动误差.本文中，齿轮微观修形包括小齿轮和大齿轮的齿顶抛物线修缘和小齿轮或大齿轮的齿向鼓形.最小的齿顶修缘量Cαa由平均啮合变形量预估，如式(4)所示.

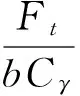
(4)

式中：Ft为切向力，N；b为齿宽，mm；Cγ为综合啮合刚度，N/mm/um，推荐值16～18 N/mm/um.

平均啮合变形量是对齿顶修缘量的一个很好的初始估计值.对于直齿轮来说，可以很好地补偿弹性变形量.对于斜齿轮来说，平均啮合变形量应在这基础上除以切向重合度εα.如果最小接触应力是优化目标，应考虑使用系数KA和齿向载荷分布系数KHβ计算峰值啮合变形量.

齿向鼓形量定义为由制造误差导致的啮合错位量的一半，从而得到较均匀的齿向载荷分布.

3 结果和讨论

首先，计算轴向重合度对接触线长度变化的影响，因为接触线长度变化会导致齿轮振动和噪声;然后，计算和比较齿轮的传动误差，确定轴向重合度对传动误差的影响关系:之后，考虑实际齿轮的啮合错位量(fma=15 μm)和微观修形，计算和对比齿轮传动误差，从而确定最优轴向重合度.具体结果如表2所示.

表2 齿轮的接触线长度变化与传动误差结果

以直齿轮和轴向重合度为0.8的斜齿轮为例，接触线长度如图3和图4所示.

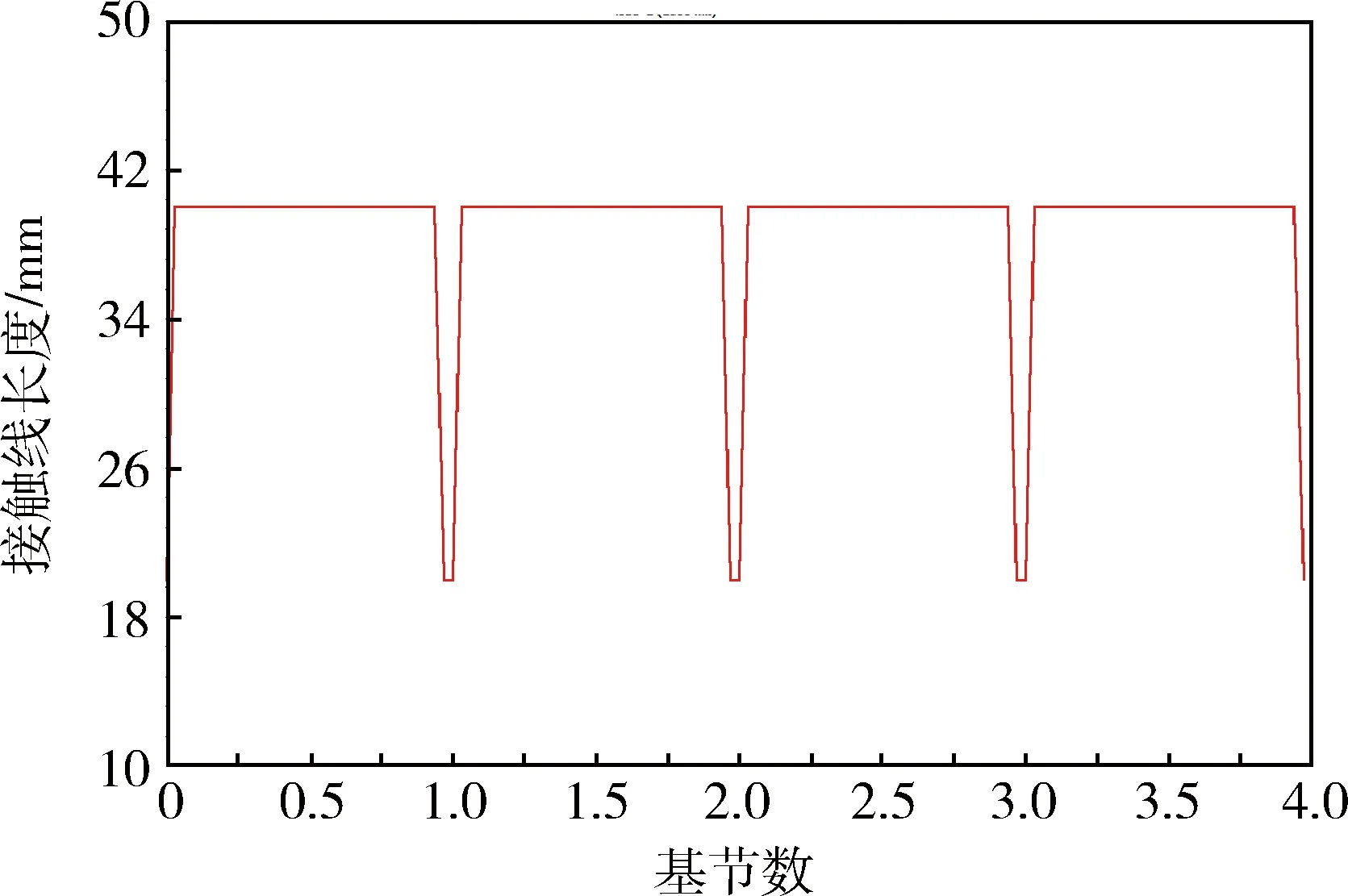
图3 直齿轮的接触线长度(切向重合度小于2)

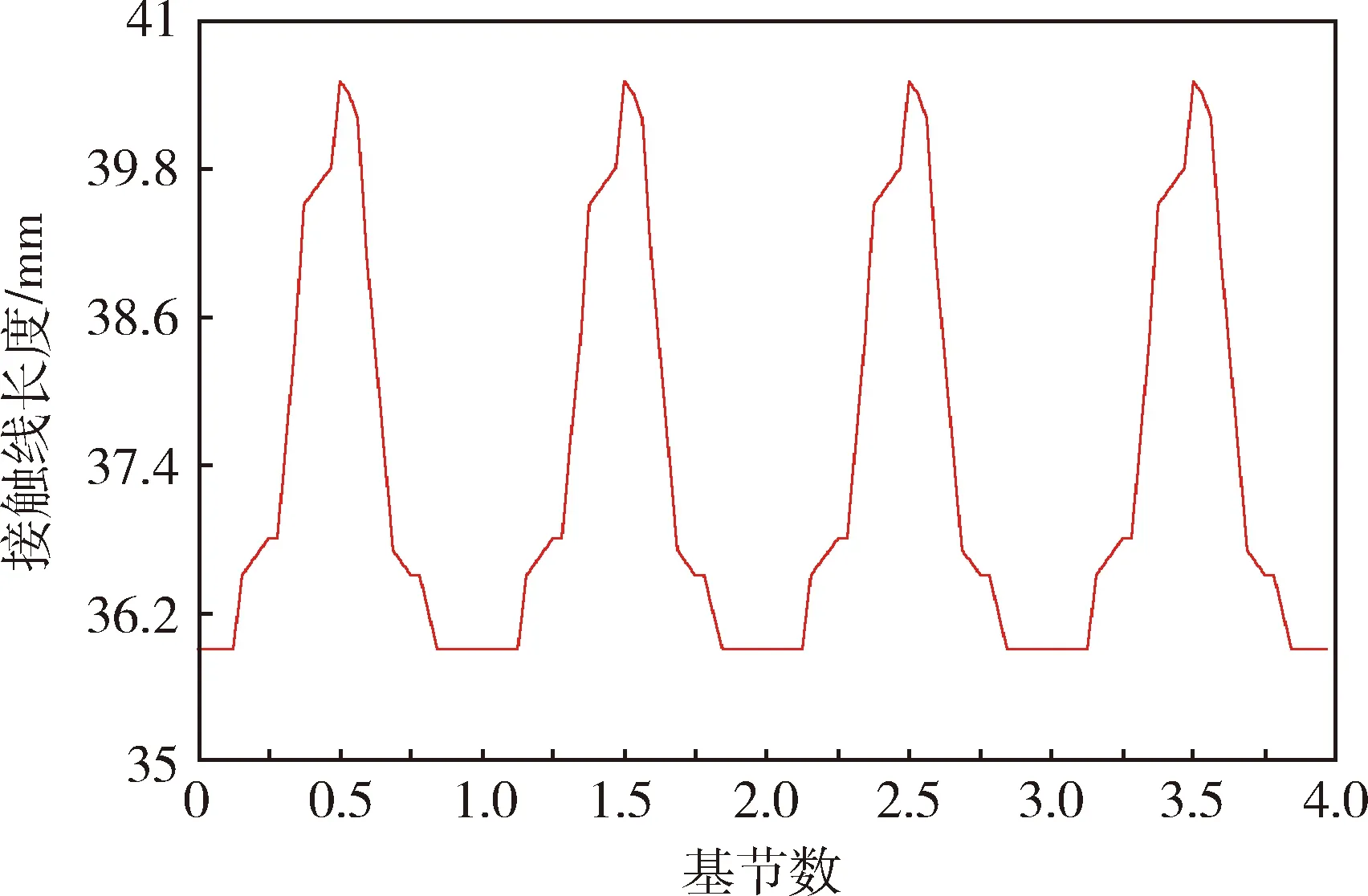
图4 轴向重合度为0.8的斜齿轮的接触线长度

由图3可以看出:最大的接触线长度为40 mm，等于齿宽(20 mm)的2倍，意味着两对齿轮同时接触.最小的接触线长度为20 mm，等于一个齿宽的长度，意味着只有一对齿轮接触，峰峰值接触线变量为20 mm.可以明显看出，接触线变化非常突然.

由图4可以看出，对于轴向重合度为0.8的斜齿轮，最大的接触线长度为40.5 mm，最小的接触线长度为35.9 mm，峰峰值接触线变量为4.6 mm.同时可以看出此齿轮接触线长度的变化相对于直齿轮来说更加平缓.

以直齿轮和轴向重合度为1.0的斜齿轮为例，齿轮传动误差如图5和图6所示.

对于这个直齿轮，由图5可以明显的看出:最大的传动误差为91.439 μm，最小的传动误差为63.739 μm，峰峰值传动误差为27.7 μm.傅里叶变换(FFT)通常被用于解释传动误差结果，表征齿轮啮合频率和谐波.从图5中也可以看出传动误差的阶次和一阶传动误差为8.995 μm.

图5 直齿轮的传动误差

对于轴向重合度为1.0的斜齿轮，由图6可以看出:最大的传动误差为113.383 μm，最小的传动误差为111.277 μm，峰峰值传动误差为2.116 μm，远远小于图5所示的直齿轮的峰峰值传动误差(27.7 μm).一阶传动误差0.591 μm，也远远低于直齿轮的一阶传动误差(8.995 μm).

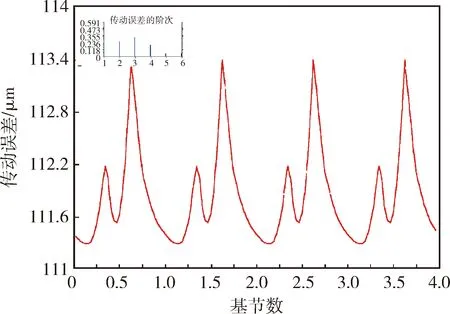
图6 轴向重合度为1.0的斜齿轮的传动误差

为了更加直观地对比结果，接触线长度的变化和峰峰值传动误差如图7、图8和图9所示.

从表2和图7(a)可以看出:斜齿轮的接触线长度的变化值相对于直齿轮来说，有很大幅度的降低.对于直齿轮和轴向重合度为0.8的斜齿轮，接触线长度的变化值由20 mm降为4.6 mm.对于斜齿轮，接触线长度的变化比较小，当轴向重合度由0.8变到1.2时，接触线长度的变化仅从4.6 mm到1.4 mm.

从表2和图8(a)可以看出:对于不考虑啮合错位量的斜齿轮和直齿轮，峰峰值传动误差有明显的降低.当轴向重合度由0变到0.8时，峰峰值传动误差由27.7 μm降为4.575 μm.对于斜齿轮来说，峰峰值传动误差的变化值仅为2.589 μm，当轴向重合度由0.8变到1.2时，峰峰值传动误差由4.575 μm降为1.986 μm.

从图7(b)可以看出:当轴向重合度接近整数1.0时，齿轮接触线长度的变化值较小.相对应的峰峰值传动误差也有相同的趋势，即轴向重合度接近整数1.0的齿轮的峰峰值传动误差较小，如图8(b)所示.

从表2、图9(a)和图9(b)可以看出:考虑齿轮啮合错位量和适当的微观修形时，轴向重合度接近1.0的齿轮的峰峰值传动误差也比较小.当考虑齿轮的啮合错位量和适当的微观修形时，轴向重合度为0.98和1.0的齿轮的峰峰值传动误差小幅度增加，这是因为齿轮在啮合错位量和微观修形的影响下，实际轴向重合度降低，略微小于整数1.0.

图7 不同轴向重合度齿轮的接触线长度变化值曲线

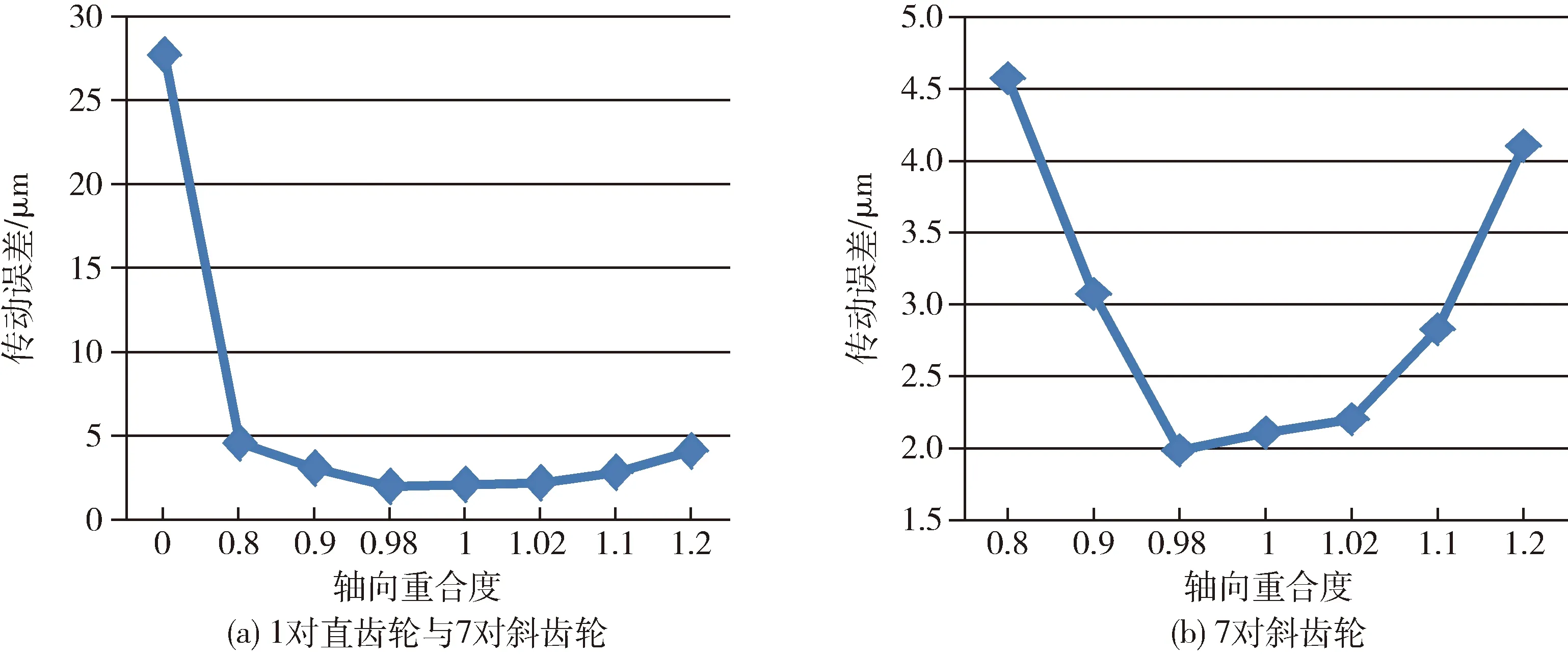
图8 不同轴向重合度齿轮的峰峰值传动误差曲线(无啮合错位量)

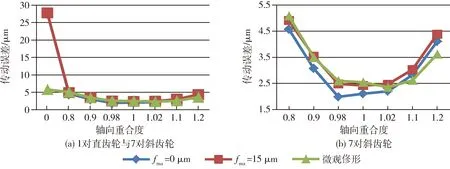
图9 不同轴向重合度齿轮的峰峰值传动误差曲线(考虑啮合错位量和微观修形)

从图9(b)还可以看出，当轴向重合度大于1.1时，可以获得较小峰峰值传动误差的优势明显减弱.因此，从获得最小传动误差的角度考虑，轴向重合度为1.02～1.05较好.

4 结 论

从以上的对比分析结果中，可以看出齿轮轴向重合度和传动误差有如下的关系：

1)在相同载荷强度下，与斜齿轮相比，直齿轮的峰峰值传动误差明显较高.这是因为，对于切向重合度小于2的直齿轮，接触线长度的变化值较大，等于齿轮的齿宽长度，因为齿轮在啮合过程中，接触齿轮对的变化为：2对齿接触—1对齿接触—2对齿接触.

2)斜齿轮可以降低齿轮啮合过程中接触齿轮对数的突变，接触线长度的变化更加平缓，从而降低动态载荷.因此，斜齿轮相对于直齿轮来说，更加能降低振动噪声.

3)对于斜齿轮，轴向重合度接近1.0时，齿轮传动误差较小，因为此时齿轮的接触线长度接近固定值.

4)考虑齿轮啮合错位量和适当的微观修形时，轴向重合度接近1.0的齿轮的峰峰值传动误差也比较小.但是，当轴向重合度大于1.1时，可以获得较小峰峰值传动误差的优势明显减弱.因此，推荐轴向重合度为1.02～1.05.

对于轴向重合度为2、3、4……的斜齿轮也可能有相同的趋势，但是这需要增加齿宽或螺旋角，从而增加啮合错位和较高轴向力的风险.接下来的工作中，计划对轴向重合度为整数2、3、4……的斜齿轮进行进一步研究.

[1] Mats Henriksson. Transmission error as gear noise excitation [C].//Proceedings of the ASME2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Confer-ence, San Diego, California, USA, IDETC/CIE 2009.

[2] Yin Jia. Analysis of Gear Static Transmission Error and Mesh Stiffness [J]. Mechanics and Materials, 2013, 365-366: 327-330.

[3] Y A Tesfahunegn. The effects of the shape of tooth profile modifications on the transmission error, bending, and contact stress of spur gears [J]. Mechanical Engineering Science, 2009,224(C): 1749-1758.

[4] P.Velex. Some Analytical Results on Transmission Errors in Narrow-Faced Spur and Helical Gears: Influence of Profile Modifications [J].Journal of Mechanical Design, 2011, 133 (3): 123-130.

[5] Ulrich Kissling. Effects of Profile Corrections on Peak-to-Peak Transmission Error [J].GEARTECHNOLO-GY, 2010, (7): 52-61.

[6] R.C.Frazer, B.A.Shaw, D.Palmer and M.Fish. Opt-imizing Gear Geometry for Minimum Transmission Error, Mesh Friction Losses and Scuffing Risk through Computer-Aided Engineering [J]. GEARTECHNOLO-GY,2010,(8):58-67.

[7] ISO 6336-1:2006, Basic principle, introduction and general influence factors [S/OL].

[8] Welbourn, D. B. Fundamental knowledge of gear noise-a survey [C]. // Proc. Noise and vib.of Eng.and Trans., IMechE, Cranefield, UK. 1979: 9-14.

[9] Dontyne Systems, Gear production suite brochure [EB/OL].http://www.dontynesystems.com/gear-design-software/.(2012).

[10] P Maillardet and D A Hofmann. A new tool for designing quiet, low vibration main propulsion gears [C]. //INEC 1996.

[11] ISO 21771:2007, Gears- Cylindrical involute gears and gear pairs-Concepts and geometry [S/OL].

[12] ISO 1328-1.Cylindrical Gears-ISO System of Accuracy. Part 1: Definitions and Allowable Values of Deviations Relevant to Corresponding Flanks of Gear Teeth [S/OL].

InfluenceofGearOverlapRatioonTransmissionError

ZHAO Lay-ue, DU Ming-gang, YANG Yang, BIAN Jix-uan

(Science and Technology on Vehicle Transmission Laboratory，China North VehicleResearch Institute，Beijing 100072，China)

TH132.41

A

1009-4687(2017)03-0020-06

2017-07-24.

赵腊月(1986-)，女，工程师，研究方向为传动技术.