车用BUCK变换器控制策略的研究

高晓宇， 韩志平， 田德文， 刘华源

(中国北方车辆研究所，北京 100072)

车用BUCK变换器控制策略的研究

高晓宇， 韩志平， 田德文， 刘华源

(中国北方车辆研究所，北京 100072)

针对车载高压直流电源在发动机转速、供电负载频繁发生突变时输出直流电压产生波动的问题，提出了超前-滞后补偿策略,采用复合控制的方式对输出电压进行控制.仿真和台架试验的结果表明，该控制策略实现了在发动机转速及电源负载发生突变时对直流电源输出电压的稳定控制.

高压直流电源；BUCK变换器；超前-滞后补偿策略

Abstract：Targeting the problem of the vehicle-mounted high voltage DC power supply′s output fluctuation that caused by engine speed fluctuation or output load variation, a lead-lag compensation strategy was presented to improve the original BUCK converter control strategy by analyzing the theory of the output fluctuation. By using the composite control strategy, the output voltage of DC power supply was controlled steadily when the engine speed and load change frequently. Simulation and test results show that the control strategy is feasible and effective.

Keywords: high voltage dc power supply；BUCK converter；advanced-lag compensation strategy

随着装甲车辆的电气负载不断增加，功率不断增大，低压直流28 V电源已无法满足整车的供电需求.因此，为满足发动机转速在1 000 r/min至2 500 r/min范围内频繁变化的过程中，飞轮发电机稳定输出10 kW这一需求，研发了270 V直流电源，并通过试验台架对其进行性能测试，试验结果表明，该高压直流电源可以满足飞轮发电机输出功率为10 kW的要求，发电精度达到(270±7) V，符合设计要求.

但是，在起动/停车、加速/减速等复杂工况下，电机转速的频繁变化会使整流母线电压产生波动，而负载的变化也会对其产生较大的影响.虽然目前电压纹波符合设计要求，但是为减小电压波动，削弱转速及负载变化对于输出电压的影响，我们对BUCK变换器控制策略[1]展开进一步研究，以达到在频繁起动/停车等复杂工况下，直流电源输出电压波动减小的目的.

1 270 V高压直流电源的组成及原理

车载高压直流电源系统，由发动机、飞轮发电机、不控整流桥和BUCK斩波电路组成，其原理图如图1所示.

图1 车载高压直流电源原理图

为实现起动发电一体机控制器高精度发电的功能，采用BUCK斩波电路与三相不控整流电路级联的拓扑结构.当起动发电一体机进入发电模式运行时，采用三相不控整流器调节BUCK斩波IGBTG1的占空比D，来实现满足270 V的直流电压输出.

BUCK变换器主电路参数如表1所示.

表1BUCK变换器参数

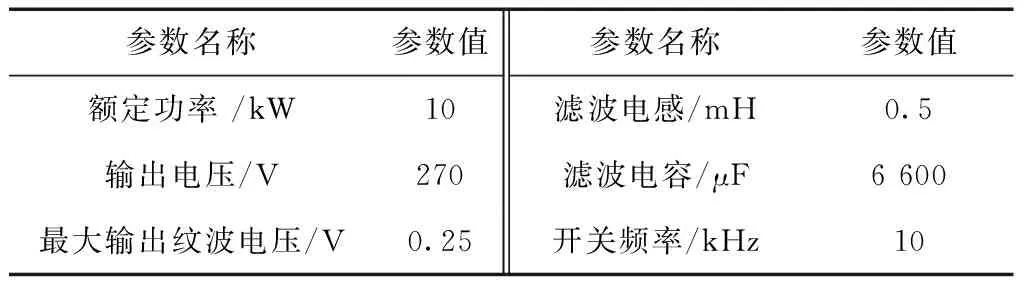
参数名称参数值参数名称参数值额定功率/kW10滤波电感/mH0.5输出电压/V270滤波电容/μF6600最大输出纹波电压/V0.25开关频率/kHz10

2 高压直流电源输出电压产生波动的机理分析

在起动/停车、加速/减速等复杂工况下，电机转速的频繁变化会使整流母线电压产生波动，而负载的变化也会对其产生较大的影响.为解决这个问题，减小输出电压的纹波电压，因此需要建立BUCK变换器动态小信号模型以及现有控制策略模型[2]，分析输出电压产生波动的机理，并对其进行仿真分析.

2.1 BUCK变换器动态小信号模型

BUCK变换器主电路如图2所示.运用扰动法建立BUCK变换器动态小信号模型.

图2 BUCK变换器主电路

图中，C1、C2为输入、输出电容；rC1、rC2为输入、输出电容等效串联电阻；L、rL为电感和电感内阻；rds为开关元器件内阻.

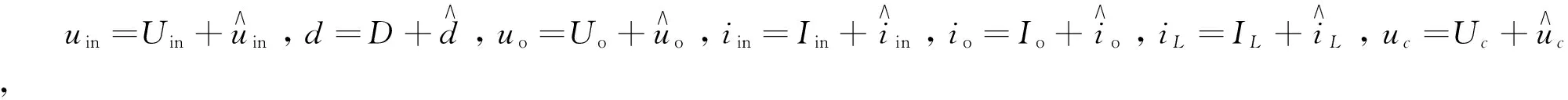
(1)

由式(1)求得系统传递函数为：

(2)

将BUCK变换器参数代入式(2)，得

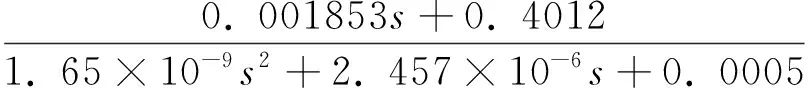
(3)

2.2 控制策略模型框图

BUCK变换器采用直接导通时间控制，控制系统闭环控制框图如图3所示.

图3 控制系统闭环控制框图

图3中，Gdo(s)为BUCK斩波电路的占空比d(s)到输出电压Uo(s)的传递函数；Gc(s)为补偿网络的传递函数；H(s)为反馈的传递函数；Hc(s)为延迟函数；ZOH为零阶保持器；To(s)为系统原始回路增益；Ts为采样时间.

系统的回路增益函数为：

T(s)=Gc(s)·To(s).

(4)

系统的开环传递函数为：

To(s)=Gdo(s)·H(s)·Hc(s)·ZOH.

(5)

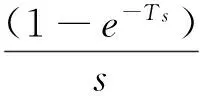
2.3 仿真结果分析

对图3所示BUCK变换器控制系统进行仿真[3]，结果如图4所示.

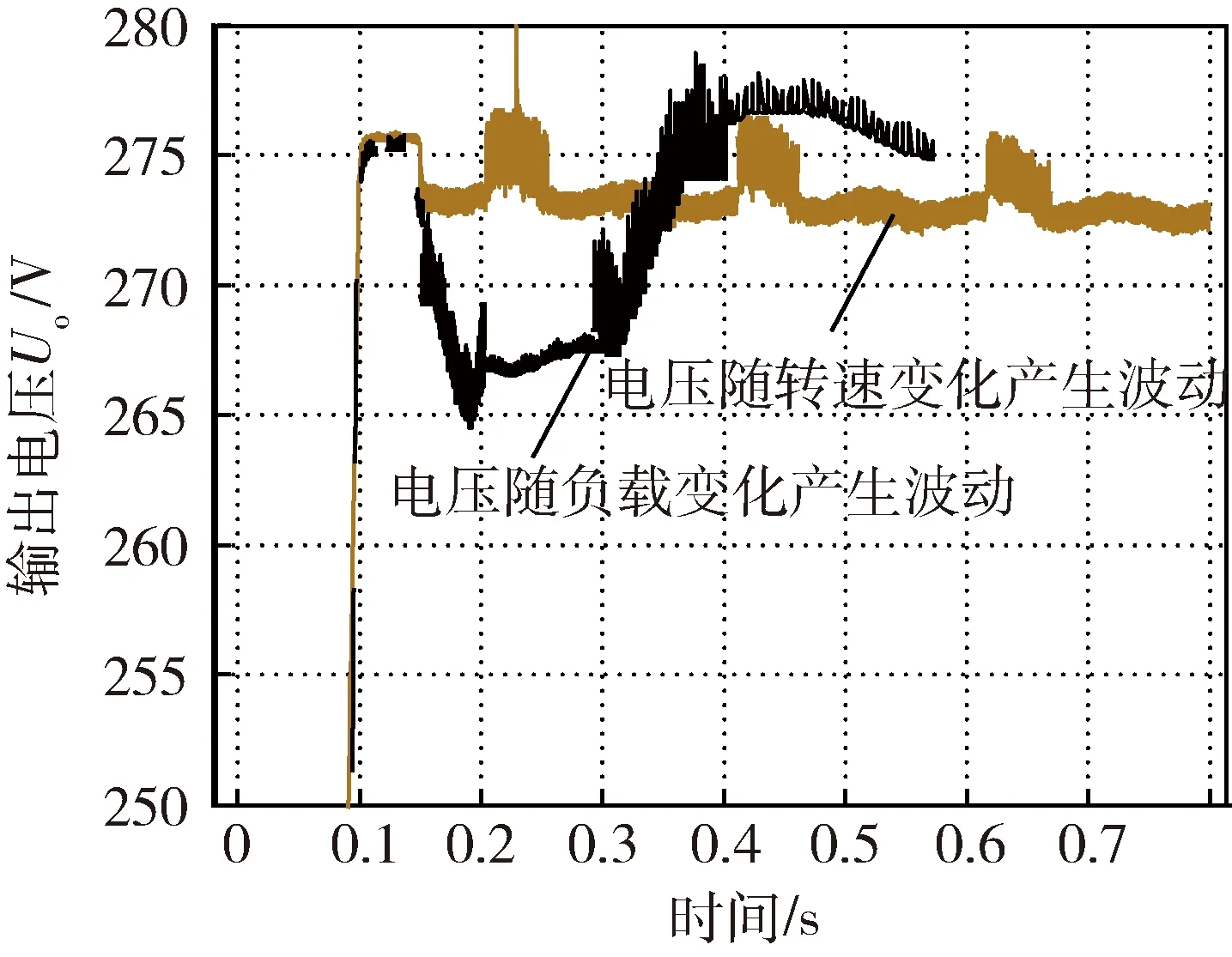
图4 现有控制系统仿真结果

由图4可以看出，在该控制策略下，直流电源输出电压符合国军标要求，但是系统响应速度较慢.当发动机转速及负载出现波动时，直流高压电源输出电压确实存在波动，系统的抗扰动能力较差[4].

3 改进后的控制策略

通过对BUCK变换器控制系统进行仿真分析，得知高压直流电源输出电压在转速/负载频发发生突变时产生波动的主要原因在于系统只采用电压环反馈控制调节输出电压，缺少补偿网络.

因此，为解决车载高压直流电源在发动机转速、供电负载频繁发生突变时输出直流电压产生波动的问题，削弱转速及负载变化对于输出电压的影响，减小输出电压波动，增强系统的抗扰动能力，同时使系统有快速的过渡响应和较强的抗扰动能力，在控制系统中增加超前-滞后补偿环节[5]，同时在反馈控制系统中增加前馈控制，引入随转速及负载变换的占空比前馈项，提高系统的稳压精度.

3.1 超前-滞后补偿器设计

设期望的补偿后相角裕度PM=58°.期望的补偿后系统开环传递函数Bode图如图5所示.由图5可知，期望的补偿后系统相角裕度PM在角速度ω为1 470 rad/s时为60.1°，幅值裕度GM在角速度ω为4 390 rad/s时为11.3 dB.

超前-滞后补偿器的控制器传递函数为

Gc(s)=Gc1(s)·Gc2(s).

(6)

图5 期望的补偿后系统开环传递函数Bode图

式中：Gc1(s)为滞后校正传递函数；Gc2(s)为超前校正传递函数.

为使截止频率附近幅值衰减，实现频域指标、改善稳定裕度及低频特性，首先进行滞后校正.取期望相角裕度PM=40°.采用一阶补偿器，其传递函数为：

(7)

已校幅值交越频率ωGC满足：

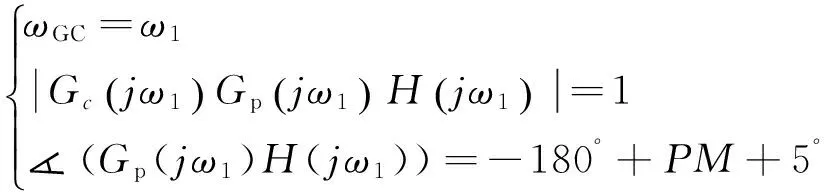
(8)

控制器增益为：

(9)

式中：ωz、ωp分别为零、极点频率.

将PM=40°代入式(9)，得到：

ω1=1 470 rad/s,ωz=147 rad/s,

ωp/ωz=0.025 8,ωp=3.799 rad/s.

可求得滞后校正后的传递函数为：

(10)

故系统加上滞后补偿器后的开环传递函数为：

(11)

加入滞后校正后系统的开环传递函数Bode图如图6所示.由图6可知，加入滞后校正后系统的相角裕度在角速度ω=1 440 rad/s时为23.5°，幅值裕度在角速度ω=2 370 rad/s时为7.32 dB.

图6 加入滞后校正后系统的开环传递函数Bode图

为了改善稳定裕度同时提高响应速度，增加系统带宽，并在滞后校正的基础上进行超前校正.取期望的相角裕度PM为58。.采用一阶控制器，其传递函数为：

(12)

(13)

(14)

在超前校正中，由于相角对加强稳定性很重要，因此最大超前角出现在已校正系统的交越频率

(15)

在ωm处控制器的增益是：

(16)

(17)

将φm=58°-23.5°+5°=40°代入式(17)，则

(18)

求解得ωm≈2 295 rad/s，ωz=1 070 rad/s，ωp=4 963 rad/s.

因此，超前校正的传递函数为：

(19)

加入超前-滞后补偿器后，系统的开环传递函数为

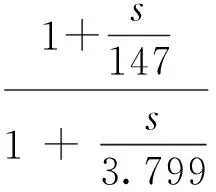
(20)

对上述的超前-滞后补偿器进行参数整定，得到系统超前-滞后补偿器的传递函数为：

(21)

加入超前-滞后控制器后，系统开环传递函数Bode图如图7所示. 由图7可知，补偿后系统的相角裕度PM在角速度ω=1 570 rad/s时为57.8°，满足系统的设计要求.

图7 采用超前-滞后补偿器后的开环传递函数Bode图

3.2 BUCK斩波电路前馈控制器设计

由于BUCK变换器控制系统运行工况较为复杂，斩波电路的输入电压发生频繁的变化，甚至存在较大输入电压波动工况，所以单纯采用直流电压闭环的超前-滞后补偿控制器无法有效满足输入电压变化时输出电压的控制精度和动态响应要求.

为解决上述问题，采用复合控制策略，在超前-滞后补偿控制器的基础上，增加随电机转速及负载变化的占空比前馈项.复合控制策略框图见图8.

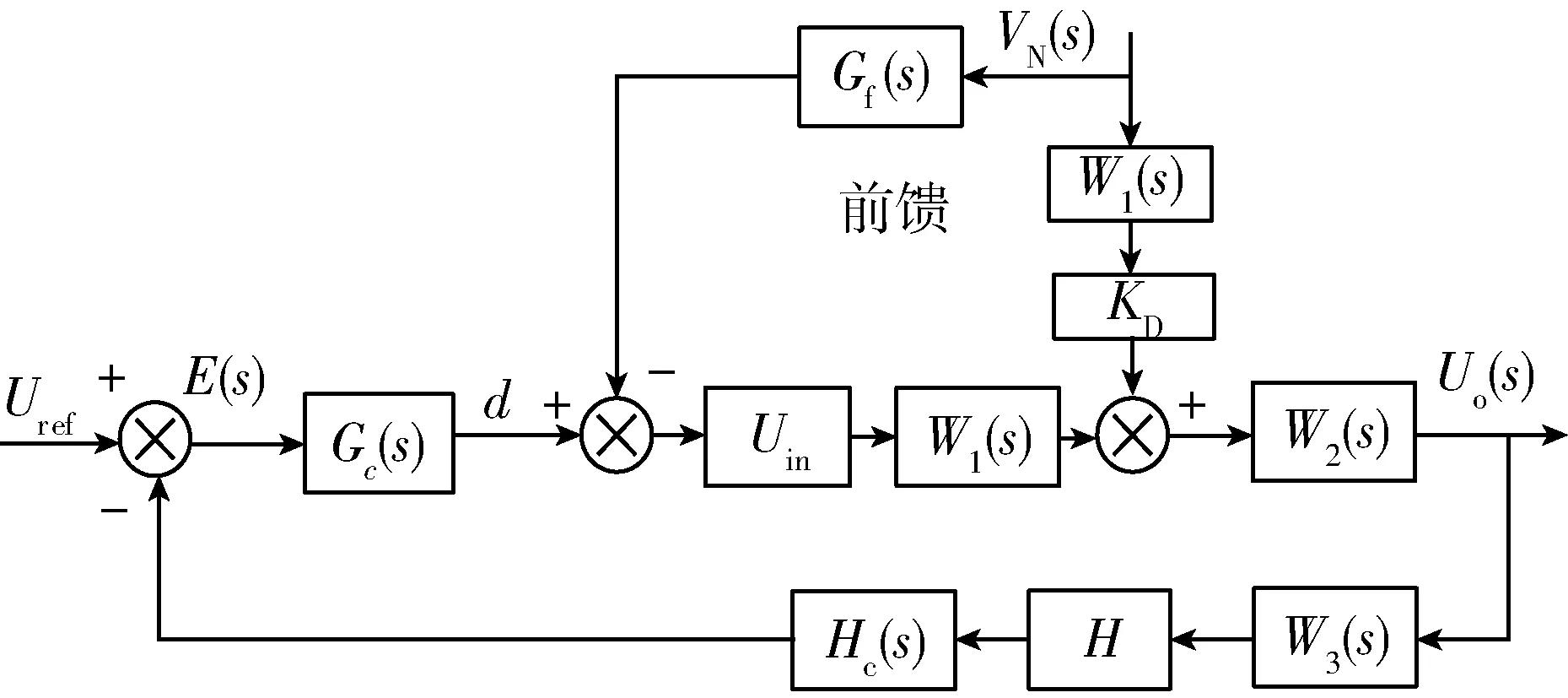
图8 转速前馈复合控制策略框图

图8中，W1(s)、W2(s)为BUCK斩波电路开关功率器件前后环节的传递函数，W3(s)为滤波器，Uin为稳态输入电压，KD为稳态占空比.由复合控制原理可知，系统的扰动误差就是给定量Uref=0时的系统输出量.由图8可求得：

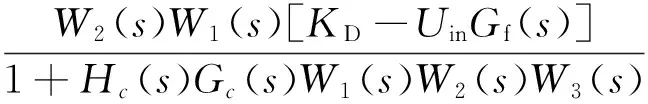
(22)

当KD-UinGf(s)=0时，得Gf(s)=KD/Uin，即采用纯比例前馈方式即可有效地抑制发动机转速变化带来的影响.当输入电压Uin=850 V时，稳态占空比为KD=0.318，前馈系数为Gf=3.74×10-4.

4 仿真并分析

4.1 转速稳压特性

针对转速变化稳压特性，在有无复合控制策略两种情况下对控制器模型进行仿真.仿真电压波形如图9所示.

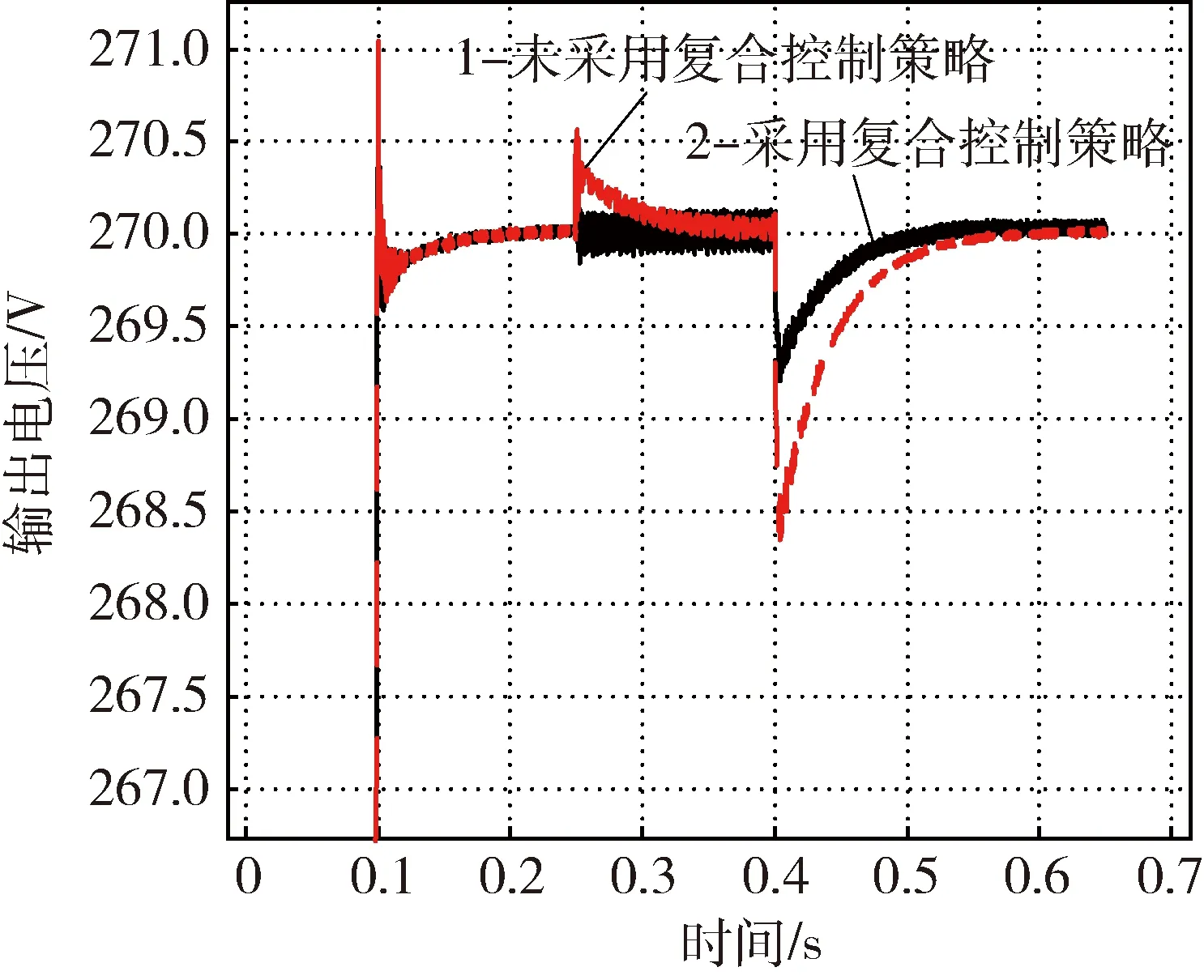
图9 转速突变下控制器输出电压波形

由图9可知：当T=0.25 s电机转速突升时，曲线1电压泵升至270.8 V，在0.37 s时恢复；曲线2电压泵升至270.1 V，在0.26 s时恢复.

当T=0.4 s电机转速突降时，曲线1电压跌至268.3 V，在0.6 s时恢复；曲线2电压跌至269.3 V，在0.52 s时恢复.

当电机转速发生突变时，采用复合控制策略后输出电压波动、恢复时间与未采用复合控制策略相比显著减小.其中，在转速突升工况下，电压波动被抑制为原值的12.5%，恢复时间缩短至原来的8.3%；在转速突降工况下，电压波动被抑制为原值的58.8%，恢复时间缩短至原来的60%.系统的转速稳压特性得到了明显改善.

4.2 突加载仿真

仿真曲线比较图如图10所示.

图10(a)给出了空载情况下发动机转速频繁变化时两种控制系统输出电压仿真曲线图.原控制系统输出电压在272～276 V范围内，新控制系统输出电压在270～275 V范围内，且曲线波动较小，明显优于原控制系统.

图10(b)给出了发动机突加载100 Ω时两种控制系统输出电压仿真曲线图.原控制系统输出电压在270～275 V范围内，新控制系统输出电压快速稳定在270 V附近，明显优于原控制系统.

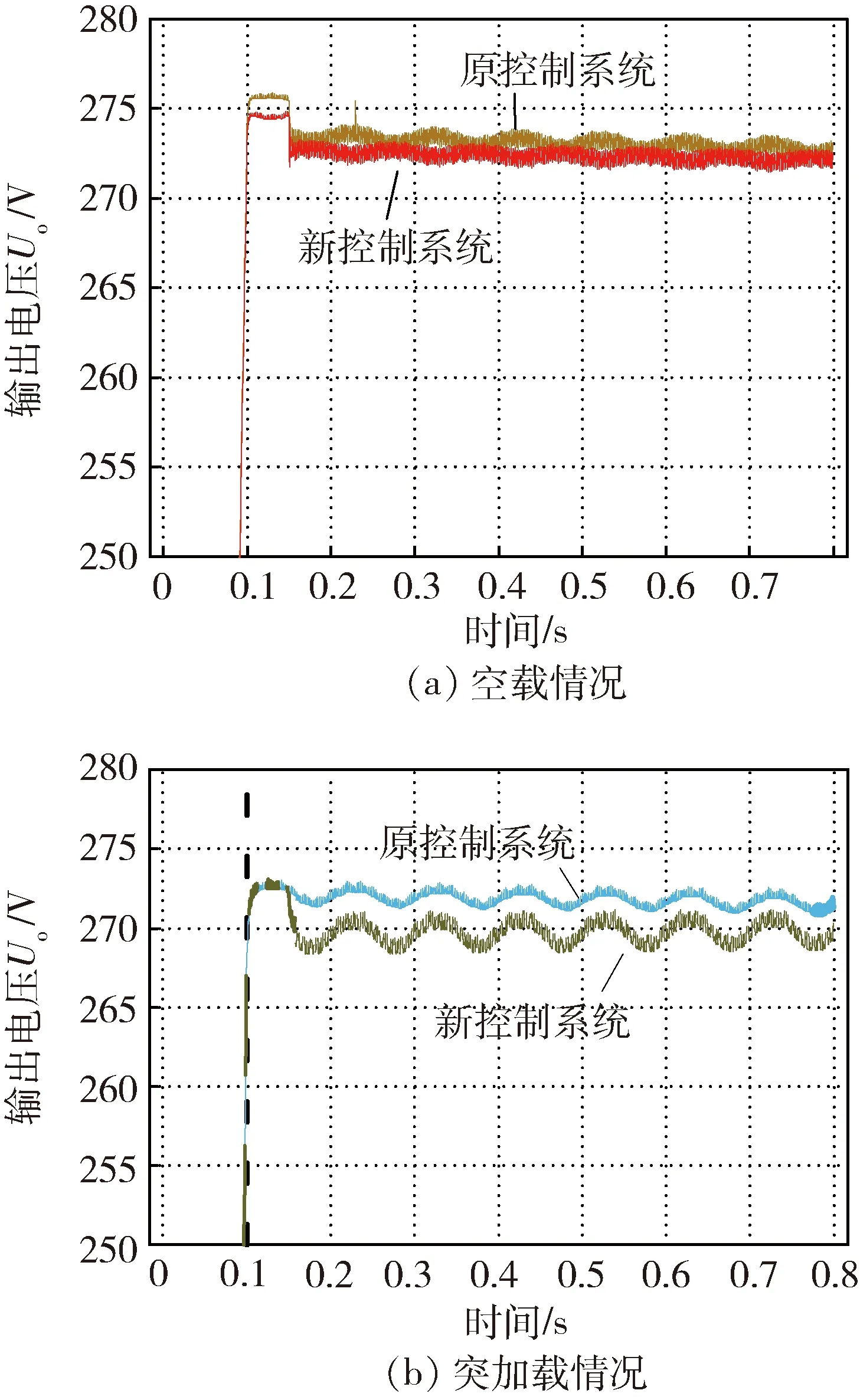
图10 仿真结果曲线比较图

5 试验分析

整个试验系统由飞轮发电机、飞轮电机控制器、超级电容、直流负载机、检测设备、动力电源等组成.

为验证控制策略的有效性，通过试验台架对BUCK变换器进行突加、突卸负载的试验.

图11为BUCK变换器的试验波形.图11(a)为突加负载试验.当变换器稳压在270 V时，进行突加负载试验，负载电流从0.8 A阶跃到32.7 A，负载电压从270 V阶跃到244.8 V，系统响应速度较快，稳定性较好.图11(b)为突卸负载试验.突卸负载后，电压由248.4 V阶跃至270 V，电流由32 A阶跃到0.4 A，整个系统的电压稳定，鲁棒性较好.

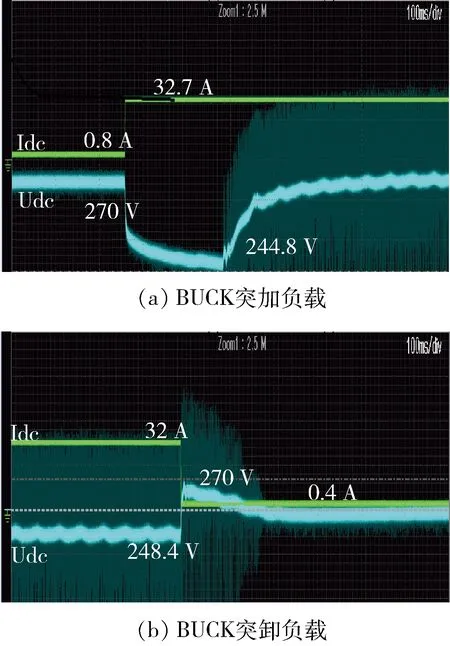
图11 BUCK变换器试验波形

由BUCK变换器试验波形可以看出，变换器拥有较快的动态响应速度和较好的稳定性.

6 结 论

针对车载高压直流电源，输出电压波动的问题，建立了BUCK变换器小信号模型，对现有控制策略加以改进，提出了一种超前-滞后补偿策略，实现了对发动机转速和电源负载突变时直流电源输出电压的稳定控制.仿真及试验结果表明,控制策略是有效的.

[1] 陈 坚.电力电子学-电力电子变换和控制技术[M].北京：高等教育出版社，2002.

[2] 张兰芸，姜孝华，何振辉，等.BUCK DC/DC 变换器的研究与设计[J]. 电力电子技术,2007.41(8):45-47.

[3] 茹东生，姜茂仁.降压型DC/DC变换器性能的仿真研究[J].青岛大学学报：工程技术版，2007,22(2):62-64.

[4] 刘树林，刘 健，寇 蕾，等.BUCK DC/DC变换器的输出纹波电压分析及应用[J].电工技术学报,2007,22(2)：91-97.

[5] 朱 杰.降压型PWM模式DC/DC开关电源的分析和设计[D].上海复旦大学，2010：16-17.

ResearchonControlStrategyofBUCKConverter

GAO Xiao-yu， HAN Zhi-ping， TIAN De-wen， LIU Hua-yuan

(China North Vehicle Research Institute，Beijing 100072，China)

U463.63

A

1009-4687(2017)03-0026-06

http：//kns.cnki.net/kcms/detail/11.4493.TH.20170710.1036.002.html

2017-03-20.< class="emphasis_bold">网络出版时间

时间：2017-07-10.

10.16599/j.cnki.1009-4687.20170710.001

高晓宇(1989-)，女，硕士研究生，主要研究方向为大功率电机驱动.