一种自主车辆横向运动状态估计的方法

刘 进， 赵熙俊

(中国北方车辆研究所，北京 100072)

一种自主车辆横向运动状态估计的方法

刘 进， 赵熙俊

(中国北方车辆研究所，北京 100072)

采用非线性三自由度单轨模型和考虑轮胎侧偏特性的非稳态轮胎模型，建立了用于状态估计的非线性状态方程.结合自主车辆的现有传感器配置，梳理了横向运动状态的观测(输入)和估计(输出).基于扩展卡尔曼滤波提出了横向运动状态估计的方法，开发了状态估计算法，实现了基于MATLAB/Simulink的离线状态估计平台.最后，通过对典型工况的仿真模拟以及对样车数据的离线回放验证了算法性能.试验结果表明算法能够合理、有效、准确地估计自主车辆行驶过程中的横摆角速度、横向速度、横向加速度、路面附着系数等横向运动状态，对车辆质量、转动惯量、路面附着系数的变化具有较好的鲁棒性.

自主驾驶车辆；横向运动状态；状态估计；扩展卡尔曼滤波

Abstract：A state estimation of autonomous vehicle′s lateral dynamics using extended kalman filter is presented, which adopted single-track 3 DOF non-linear vehicle model, as well as non-steady tire dynamic model. Based on the sensor configuration of common autonomous vehicles, measured and estimated states are determined exactly. Due to non-linear model behavior, the extended kalman filter is utilized for state estimation and an off-line state estimator based on MATLAB/Simulink is implemented. The performance of the proposed method is analyzed with simulation scenarios and real data replay. The experimental results show that the proposed method has good performance and is robust to key parameters of lateral dynamics.

Keywords: autonomous driving vehicles; lateral states；state estimation；extended kalman filter

行驶状态估计是保证自主驾驶车辆安全行驶的重要技术.对运动状态的实时准确估计不仅能改善路径跟踪控制精度，而且能提高自主车辆的运动控制和行驶安全性，特别是对极限工况下的动力学控制与安全行驶提供必要信息.自主驾驶车辆横向运动状态估计是以现有传感器配置为基础，采用多源的信息融合和先进的状态估计算法，对横向运动的状态，如横向速度、横摆角速度、轮胎侧偏力等进行精确估计的方法.

常用的各种状态估计算法有Luenberger观测器、鲁棒观测算法、滑模观测算法、神经网络和模糊观测算法以及各式各样的非线性观测器，等等.其中卡尔曼滤波理论以其独特的迭代方法已成为主流的行驶状态估计方法，它不仅可以实现在线实时计算，同时具有良好的估计精度.文献[1]在建立单轨车辆非线性三自由度车辆模型基础上，利用扩展卡尔曼滤波(Extended Kalman Filter，EKF)对纵向车速、横摆角速度和质心侧偏角进行了估计，并通过仿真和样车试验进行了验证.文献[2]采用双轨车辆模型，通过EKF对纵向车速、横摆角速度、质心侧偏角以及轮胎的纵横向力进行了估计，且实现了状态估计的在线实时系统，实验结果表明所提出的方法对模型中的参数，如质量、转动惯量、路面附着系数等的变化具有较好的鲁棒性.然而上述方法都忽略了路面附着系数变化较大的情况，例如路面附着系数减小时对估计精度影响较大，特别是路面附着系数变化时，常常需要人工调整初始值以获得期望的估计精度.

本研究提出一种自主驾驶车辆的横向运动状态估计方法，由环境感知对路面识别分类的结果给出的附着系数初始值，采用扩展卡尔曼滤波方法估计地面附着系数以及横向运动状态.这种方法大大提高了自主驾驶车辆在复杂工况行驶过程中状态估计的精度和可靠性，且所设计的状态估计算法对参数变化具有一定的鲁棒性，保证了当环境感知对路面附着条件的识别不十分精确时的状态估计精度.

1 问题的描述

充分利用自主驾驶车辆上安装的传感器有助于更好地解决横向运动状态估计问题.通过原车的CAN总线获取纵向车速u和前轮偏角δF，通过惯性测量单元(Inertial Measurement Unit，IMU)获取纵向加速度ax、横向加速度ay、横摆角速度ωr.因此，本文研究的横向运动状态估计算法的观测与估计，即输入与输出，如图1所示.所需估计的横向运动状态变量包含纵向速度u、横向速度υ、横摆角速度ωr、纵向加速度ax、前后轴侧偏力FytF和FytR,等等.状态估计的输入为直接可以测量的状态，如纵向车速u、横摆角速度ωr、前轮偏角δF、纵向加速度ax和横向加速度ay.

图1 横向运动状态估计算法输入-输出

假设自主车辆行驶在平坦路面上，只考虑纵向、横向和横摆运动.结合输入输出关系，建立三自由度横摆动力学非线性模型，

(1)

式中：m表示车辆质量；Iz表示绕z轴的转动惯量；lF为质心到前轴的距离；lR为质心到后轴的距离.

式(1)表明，非线性不仅表现在横摆运动的耦合关系上，更表现在非线性轮胎侧偏力上.特别是车辆行驶在极限工况时，轮胎侧偏力明显表现为轮胎侧偏角的非线性函数，这将导致车辆横向动力学模型的强非线性.

考虑到侧偏动特性，前后轴轮胎的侧偏力非稳态特性为[3]

(2)

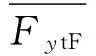
结合魔术公式中的系数和附着系数之间关系的描述[5]，纯侧偏工况下的魔术公式描述的轮胎侧偏力为

(3)

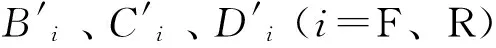
为前后轴侧偏角，对于前轮转向车辆按照αF=δF-arctan(tanβ+lFωr/u)、αR=-arctan(tanβ-lRωr/u)计算.显然，改进的魔术公式可描述不同路面附着条件下的轮胎侧偏特性.

根据对前后轴的轮胎侧偏力估计，可计算得到横向力的利用附着系数，即前后轴的横向力与垂向载荷的比值[4]，

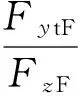
(4)

利用附着系数满足μyF≤μ、μyR≤μ，其中μ为路面附着系数.

2 横向运动状态估计的扩展卡尔曼滤波器设计

卡尔曼滤波理论应用的难点在于，噪声协方差矩阵初值、系统噪声协方差矩阵、测量噪声协方差矩阵的确定.另外，车辆参数的变化，如路面附着系数、车辆质量、转动惯量，会直接改变所建立的车辆模型输出，进而影响状态估计精度.因此，如何设计具有鲁棒性的状态估计算法是研究者们需要攻克的难题.

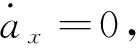
(5)

y(t)=h(x(t),δF)+v(t).

(6)

式中：状态变量x分别是x1=u，x2=υ，x3=ωr，x4=ax，x5=FytF，x6=FytR；δF为输入变量；输出变量y分别是y1=u，y2=ωr，y3=ax，y4=ay；非线性函数f(·)和h(·)分别为

(7)

(8)

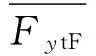
式(8)中的非线性函数f(·)和h(·)对状态变量x和干扰变量w、v求偏导，得到雅克比矩阵F、H、W和V，其中F为6×6矩阵、H为4×6矩阵、W=I6×6、V=I4×6.干扰变量w(t)、v(t)为过程噪声和测量噪声，且为相互独立、均值为零的高斯白噪声.

对F离散化处理，选取采样间隔Δt为10 ms，得到状态转移矩阵Φ(t)=eF(t)Δt≈I+F(t)Δt.通过求偏导，得到矩阵F为

(9)

其中,F5j和F6j(j=1、2、3)的计算如下，

(10)

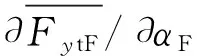
(11)

(12)

同理，可得到F52、F53和F61、F62、F63.

对于量测方程的雅克比矩阵H为

(13)

得到了矩阵F、H和Φ后，就可以运用EKF进行横向运动状态估计.EKF分为两个步骤：第一步骤为预测，是对状态的时间更新过程；第二个步骤为更新或校正，通过测量值和滤波器增益对第一步骤中预测的状态进行更新.EKF从已知的状态初始值x0和状态协方差矩阵初始值P0开始进行计算，反复执行预测-校正步骤，故滤波过程实际上是基于状态变化为一阶马尔科夫过程假设的“预测-校正”的反馈控制器.算法的计算过程如图2所示.图中x为状态变量；u为输入向量；y为观测向量；Q表示激励噪声w(t)的协方差矩阵；R表示测量噪声v(t)的协方差矩阵；K为卡尔曼增益；P为估计误差方差矩阵；F和H分别按照式(9)和式(13)计算.

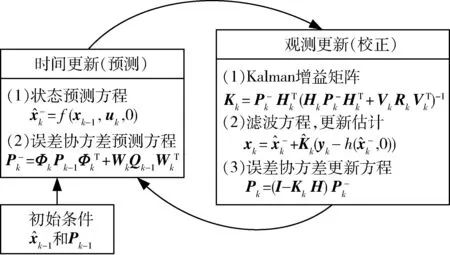
图2 EKF的计算过程

3 试验结果与分析

为测试文中提出方法的有效性，通过MATLAB/Simulink搭建状态估计测试环境，实现状态估计算法，并通过仿真数据和样车数据对状态估计方法进行离线验证.

在仿真分析中搭建CarSim和MATLAB/Simulink的联合仿真平台，用CarSim模拟车辆动力学系统，用噪声模拟传感器采集数据.车辆参数如表1所示.

表1 车辆参数

3.1 仿真试验

仿真工况选取为CarSim软件自带的双移线试验工况：1)车辆行驶速度为30 m/s；2)车辆行驶在良好路面上，路面附着系数为μ=0.9；3)自主车辆按照双移线试验所规划的路径行驶.

双移线仿真试验的结果如图3所示.

从图3(a)中看出，EKF估计值能够较好地跟踪测量值，从带有噪声的观测量中估计出较为平滑的车辆状态.图3(b)为无法直接测量的车辆横向运动状态.从图中看出，EKF估计值能够较好地跟踪CarSim车辆模型状态值.前后轴横向力和横向利用附着系数的估计值与状态值具有一致性趋势.特别是，υ和β的估计曲线与状态曲线基本一致，表明EKF算法能够很好地估计车辆横向运动状态.

下面分析双移线试验中EKF对参数变化的鲁棒性.图4为3个参数m、Iz和μ分别取额定值的85%、100%和115%时，4个输出量u、ωr、ax和ay的估计值与测量值之间误差的标准差.图中表示随着参数的增加或减小，输出量的估计值与测量值之间误差的标准差也相应增加，但是EKF算法仍能保持较好的性能.也就是说参数的变化会降低EKF算法的车辆横向运动状态估计能力，但是不至于导致EKF发散.这表明EKF算法在双移线试验工况下也对参数的有界变化具有较好的鲁棒性.

但是，如果路面附着系数的变化范围更大，例如路面附着系数降低到0.6或以下，此时EKF初值路面附着系数仍取0.9，那么EKF算法将发散.其原因是由于EKF中计算的理论轮胎模型和实际轮胎模型之间存在较大偏差，导致车辆所受的横向力和横摆力矩与实际值相差甚远，所有计算完全偏离实际情况.此时须通过环境感知对道路分类结果来修正路面附着系数的初值.

3.2 样车试验

采集了所开发的自主车辆在某良好路面上自主驾驶时的行驶状态，并通过MATLAB/Simulink环境下的EKF算法进行离线状态估计.

图5为基于样车试验数据的离线EKF状态估计结果.图5(a)表示EKF估计值与样车试验测量值曲线.从图中看出，EKF估计值能较好地跟踪输出量.特别是纵向加速度ax和横向加速度ay存在粗大误差的情况下，EKF仍能获得较好的估计结果.图5(b)表示EKF估计值与模型状态值的曲线.状态值根据所采集的车速和前轮偏角的数据，通过搭建的CarSim车辆模型计算得出.状态值主要计算无法直接测量的横向速度υ和质心侧偏角β.从图5看出，EKF估计值(υ和β)与状态值的变化趋势完全一致，表明EKF状态估计性能较好.

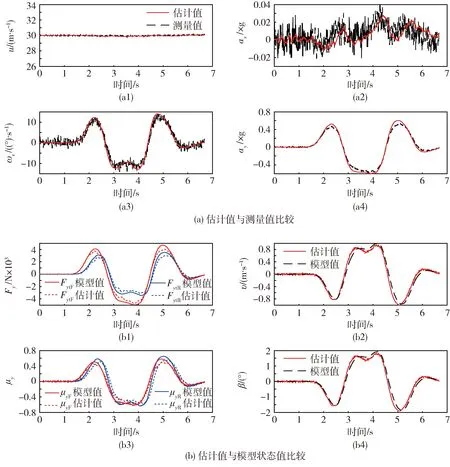
图3 双移线工况的仿真结果

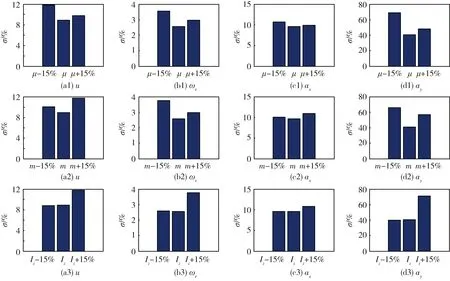
图4 EKF对参数变化的鲁棒性试验结果

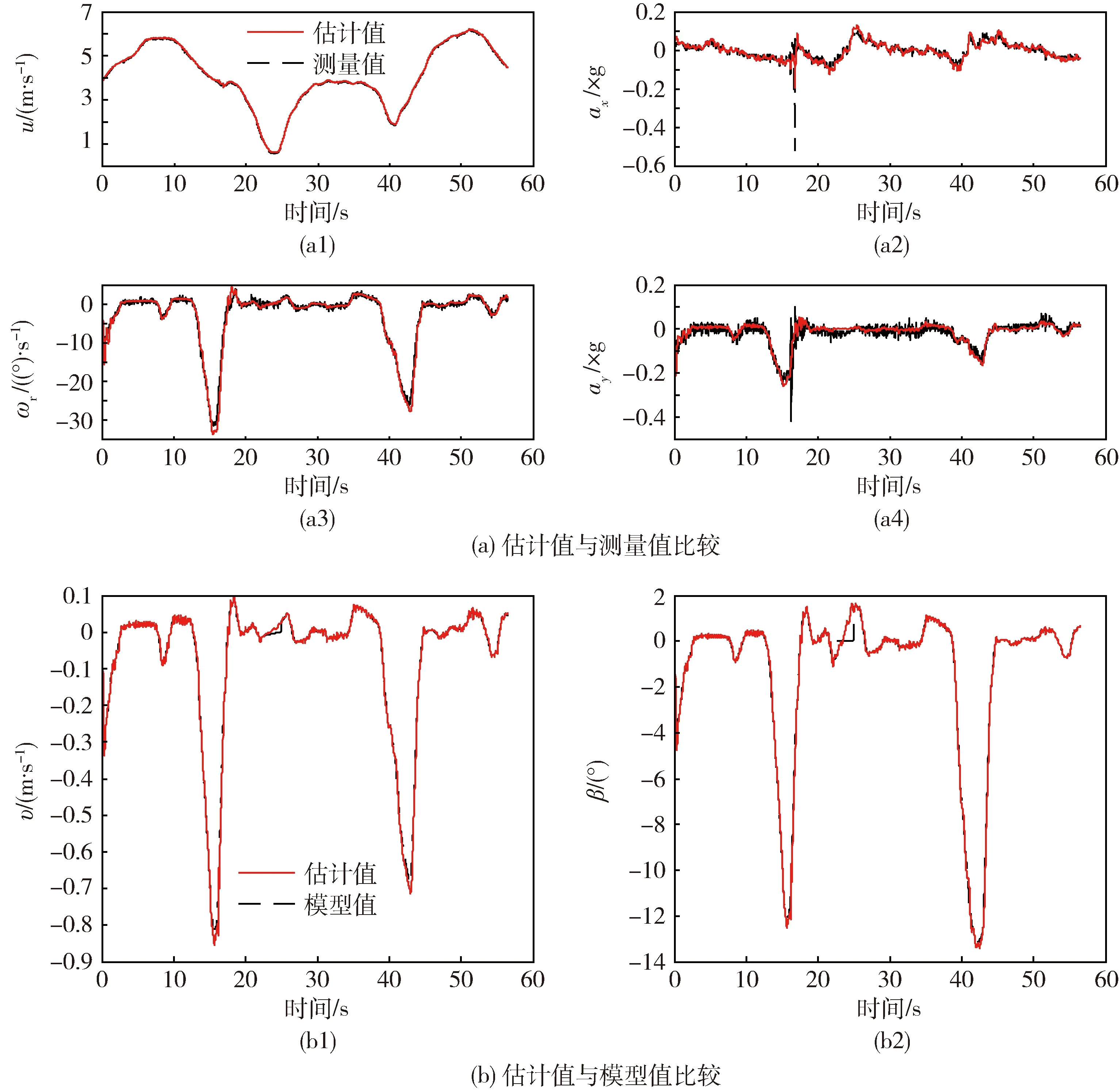
图5 样车试验数据的离线计算结果

图6表示样车试验测量值与EKF状态估计值之间误差的标准差.从图6中看出，车速u和横摆角速度ωr误差的标准差较小，而纵向加速度ax和横向加速度ay误差的标准差较大.这是由传感器的精度和噪声引起的.加速度传感器的测量噪声比较大，因此EKF平滑后误差的标准差自然就大.图6的结果表明样车试验的EKF估计具有良好的性能.

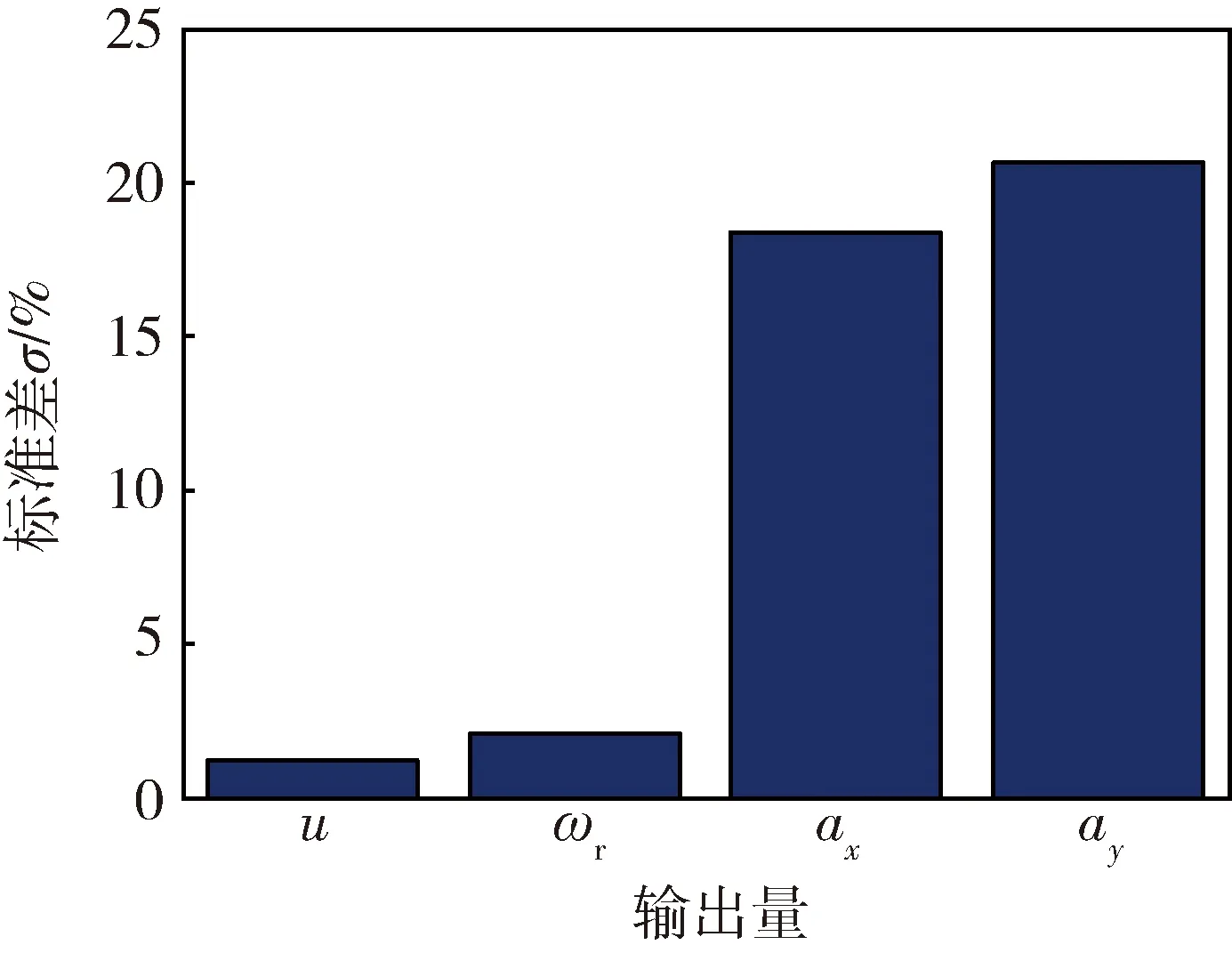
图6 EKF样车试验性能

4 结束语

基于纵横向耦合运动的三自由度非线性车辆单轨模型和非稳态轮胎模型，以自主车辆现有传感器的测量信息为基础，运用扩展卡尔曼滤波理论，研究了一种自主车辆横向运动状态估计方法，通过仿真测试和样车试验验证了算法性能.试验数据表明，该方法对车辆质量、转动惯量、路面附着系数在-15%～+15%范围内变化时能够合理、准确地估计横摆角速度、横向速度、前后轴侧偏力等横向运动状态.实际上，路面附着系数在-50%～+50%范围内变化时，所提出的状态估计方法也都具有较好的鲁棒性，能够准确估计车辆横向运动状态；路面附着系数变化范围超过50%以上时，由于轮胎模型和实际轮胎侧偏力之间的较大偏差会导致本研究提出的EKF不收敛，此时须利用自主车辆环境感知系统对路面材质和附着特性进行识别，为状态估计提供更合理的初值.只要能够保证初值给出的附着系数不超过真值的50%，那么所提出的算法能就保证横向运动状态估计的准确度.所提出的状态估计方法为车体运动控制、行驶安全性控制、路径跟踪控制、在线故障诊断提供反馈信息，有助于提高自主车辆的控制性能和行驶安全性.

[1] 宗长富, 潘 钊, 胡 丹, 等. 基于扩展卡尔曼滤波的信息融合技术在车辆状态估计中的应用[J]. 机械工程学报, 2009, 45(10): 272-277.

[2] Doumiati M, Victorino A.C, Charara A, et al. Onboard Real-Time Estimation of Vehicle Lateral Tire-Road Forces and Sideslip Angle[J]. IEEE/ASME Transaction on Mechatronics, 2011, 16(4): 601-614.

[3] Rill G. First Order Tire Dynamics[C]//European Conference on Computational Mechanics Solids, Struct-ures and Coupled Problems in Engineering. Lisbon: 2006: 1-9.

[4] Mitschke M, Wallentowitz H.汽车动力学[M].4版. 陈荫三, 余 强,译. 北京:清华大学出版社 2009: 5-42.

[5] Jagt PVD, Parsons AW. Road Surface Correction of Tire Test Data[J]. Vehicle System Dynamics, 1996, 25(2): 147-165.

StateEstimationofLateralDynamicsforAutonomousVehicles

LIU Jin， ZHAO Xi-jun

(China North Vehicle Research Institute, Beijing 100072, China)

U270.1+1

A

1009-4687(2017)03-0001-07

2017-06-01.

刘 进(1971-)，男，研究员，研究方向为地面无人平台技术.

赵熙俊(1984-)，男，副研究员，研究方向为地面无人平台自主技术.