POE策略下的数学教学实践

☉江苏省海门市四甲中学 夏 华

POE策略下的数学教学实践

☉江苏省海门市四甲中学 夏 华

皮亚杰早期提出过概念同化理论，其认为学习者在学习过程中历经了认知平衡—认知冲突—重新平衡的过程，这在很长一段时间内被教育界认同.特别是像数学这样的抽象学科，其头脑中的知识是一步一步螺旋叠加的，要将新的知识与头脑中固有的知识进行完美的衔接，需要接受新知、新方法对固有知识体系的冲击，这种冲击会带来新的知识平衡，恰恰是皮亚杰研究的概念同化理论.

进一步来说，皮亚杰概念同化理论的发展说明了我们对知识理解的平衡性，在一个动态的、发展的过程中寻求平衡.那么怎么样实现、获得平衡的呢？学者Gunstone和White在研究概念同化理论的过程中，提出了知识学习过程中的POE策略，其建议首先采用了Prediction（预习感知），这种感知可以让学习者具备一定的形象性；其次是Observation（思考分析），这恰恰是建议要实现这种同化需要做的思维过程；最后是Explanation（归纳小结），将新获得的知识融入到自身现在的体系中，形成全新的知识体系，这样的学习策略强化了同化理论.实践表明，POE策略在数学学习的过程中，特别是抽象数学学习的过程中，形成了严密的学习步骤和过程.

一、POE策略在知识深化中的实践

课程理念表明，数学的学习是螺旋式上升、循序渐进的.这一科学的学习理念让我们认识到数学学习必须有一定的步骤性，以往教师一股脑儿将知识和技能全倒给学生的做法，是不被认可的.根据心理学研究发展理论来说，在知识全部获取过程中，运用合理的策略将知识教学的深度进行充分挖掘，以便实现知识深化的过程.

教学案例1：线性区域的最值研究.

问题（Prediction）：已知点P（x，y）所在区域D满足条件求z=2x+y的最值.

分析：z=2x+y⇒y=-2x+z，作可行域如图1.

由图可知，在点B（1，1）处，目标函数有最小值3；

图1

在点C（5，2）处，目标函数有最小值12.

意图：以学生熟练掌握的线性规划基本问题入手，回顾思考目标函数的几何意义，在图形中寻求解决问题解决基本方式——几何法.

变式1（Observation）：已知点P（x，y）所在区域D满足条件求下列目标函数的取值范围：

（1）z=|x+y-3|；（2）z=（x+2）2+y2；（3）z=

分析：（1）师：目标函数z=|x+y-3|体现了什么样的几何意义？

生：截距的绝对值？

师：这位同学所说的是它的代数意义，并不是几何意义，几何意义指的是图形中的含义.

生：可以从点到直线的距离公式中思考.

师：好！思考非常到位，请具体说一说处理过程.

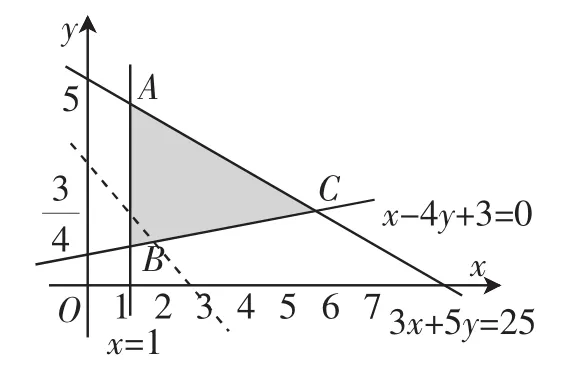
图2

（2）师：有了前面问题的铺垫，我们可以进一步思考不同目标函数的几何意义理解和处理.这一目标函数z=（x+2）2+y2所体现的几何意义是什么呢？

生：这个容易，应该表示P（x，y）到定点（-2，0）的距离的平方.

师：好！思考非常到位，请具体说一说处理过程.

图3

生：这个和我们刚刚学过的两点间的斜率公式有关.

师：好！思考非常到位，请具体说一说处理过程.

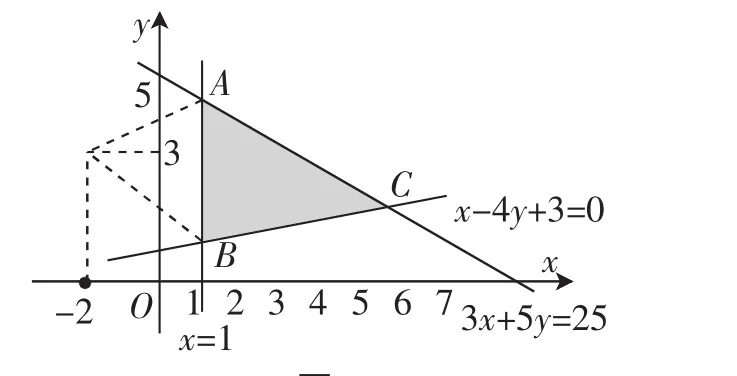
图4

意图：在基本的线性问题感知后，运用变式教学手段，加入了问题的思考，即POE学习策略中积极思考分析的过程，加深了知识的深度，理解和掌握了目标函数从感知到思考分析的过程，形成了目标函数在头脑中一定的处理体现.

小结（Explanation）：将常见线性区域问题目标函数最值的处理，进行反思总结：

（1）z=ax+by+c几何意义体现的是直线的截距；（2）z=|ax+by+c|几何意义体现的是点到直线的距离；（3）z=（x-a）2+（y-b）2几何意义体现的是点与点之间的距离；几何意义体现的是两点间连线的斜率.对进一步知识的深度思考，让学习对线性区域下的目标函数最值有了更深度的思考和理解，让目标函数的几何意义有了深思和掌握.

变式2（再反思）：已知f（x）=ax2+cx，且1≤f（1）≤3，-1≤f（-1）≤1，求f（2）的取值范围.

错解：本题是学生初学不等式中教材的习题，学生普遍的错误率是如下求解单量：由已知可得

①+②，得0≤2x≤4，即0≤4x≤8，

②×（-1），得-1≤y-x≤1.③

①+③，得0≤2y≤4.

故而代入f（2）=4x+2y，得0≤f（2）≤12.

这种单量研究的过程显然大大扩大了解的过程，此时请学生进一步思考线性区域的目标函数处理，从而理解错解产生的原因.

解：由已知可得3≤3f（1）≤9，-1≤f（-1）≤1，不等式组的可行域可以轻松获得，故而可得2≤f（2）≤10.

意图：回归教材基本问题，让学生思考和理解了目标函数真正的应用价值，通过POE策略，感知基本到思考分析到巩固小结，到问题的再反思，体现了知识的深度性，利用POE策略实现了教学的深层次.

二、POE策略在知识抽象中的实践

高中数学具备了较强的抽象性，在较强的抽象性中获得知识的理解和运用是困扰学习者的因素.比如学生对抽象函数的理解不如具体函数到位，对平面向量基本定理的理解往往侧重正交分解下的坐标形态等等，这些都阻碍着学生进一步的思维发展，笔者认为用POE策略可以加强学生思维的层次性.

教学案例2：（1）函数f（x）的定义域为（1，2），求函数f（x+2）的定义域.

（2）函数f（x+1）的定义域为（-∞，1］∪［2，+∞），求函数f（x-1）的定义域.

运用POE教学策略研究：从抽象函数的问题来看，学生往往不理解和不掌握，这种困扰是其本身对函数概念的掌握程度不够造成的.从笔者多年一线教学经验来看，抽象函数部分的教学比较适宜的是给学生搭建足够多的“感知脚手架”，有了这一工具，学生自然而然地获得了更为充分的理解.

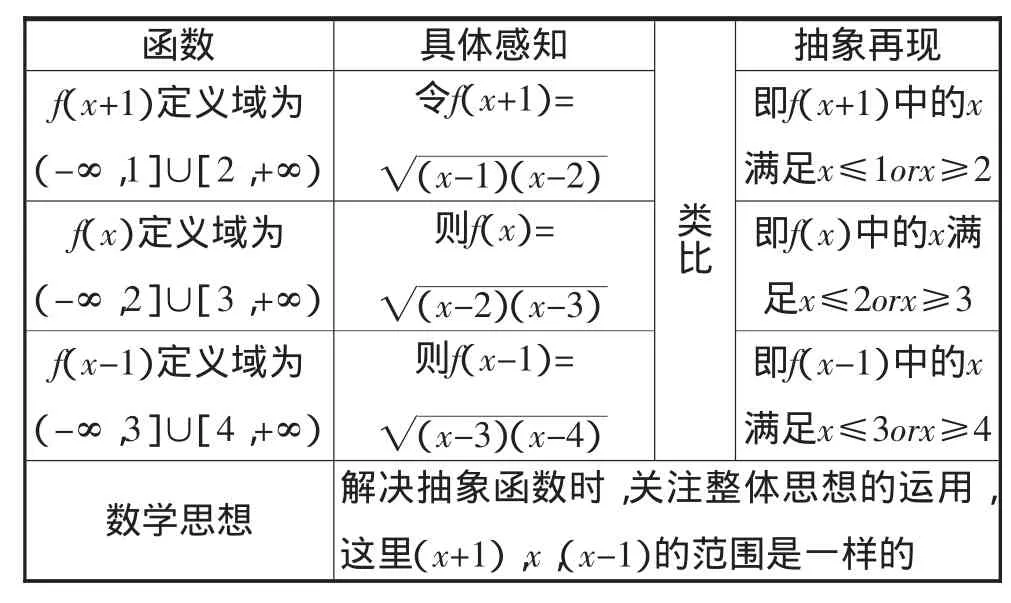
函数 具体感知类比抽象再现f（x+1）定义域为（-∞，1］∪［2，+∞）令f（x+1）=（x-1）（x-2）即f（x+1）中的x满足x≤1orx≥2 f（x）定义域为（-∞，2］∪［3，+∞）则f（x）=（x-2）（x-3）即f（x）中的x满足x≤2orx≥3 f（x-1）定义域为（-∞，3］∪［4，+∞）则f（x-1）=（x-3）（x-4）即f（x-1）中的x满足x≤3orx≥4数学思想 解决抽象函数时，关注整体思想的运用，这里（x+1），x，（x-1）的范围是一样的

意图：首先，抽象函数中最让学生弄不清楚的是定义域到底表达的含义是什么？笔者以上述从形象到抽象的具体表格，将问题的理解和思考达到了较为清晰的层面，这里感知——思考融合得非常完美，加深了学生对于抽象函数中定义域的理解；其次，整体思想的运用，抽象函数中法则f（*）的理解，是学生并不到位的地方，只要在符号f（*）中，其所有的变量整体都是等价的，即表述的含义是能够运用此法则的变量，因此POE策略在这样的教学中让教学变得无比朴实、易于理解.

教学案例3：（1）函数y=f（x）满足f（a+x）=f（b-x），则函数y=f（x）的图像关于_________对称.

（2）函数y=f（x）满足f（a+x）+f（a-x）=2b，则函数y=f（x）的图像关于_________对称.

运用POE教学策略研究：进一步研究与抽象函数的相关性质，我们不难发现这样的性质学生理解有困难，在实际问题的解决中也常常弄错，笔者提倡首先依旧是具体感知—思考分析—归纳小结，这样的过程加快了学生对抽象函数相关表达式的理解.

函数性质 具体感知类比抽象再现f（a+x）=f（b-x）令f（x）=x2验证直线x=a+b 2对称f（a+x）+f（a-x）=2b令f（x）=x验证点（a，b）对称

有了上述具体模型，我们还可以这样去引导学生理解：以f（a+x）=f（b-x）为例，令x1=a+x，x2=b-x，则f（x1）=f（x2），对任意的x进行变换，可知自变量中点为不变量x=，又函数值f（x1）=f（x2），因此随着x进行变换，显然f（x）关于.轴对称成立.其余类似研究，不再赘述.

总之，POE是一种教学策略，主要是关乎形式化程度不高的中学生，其较为合适地将抽象和具象完美的融合策略，使得中学数学教学获得了一个比较完整的步骤.在每一个知识点教学的背后，我们可以进行足够的感知和思考，进而获得归纳小结，这样的知识学习过程符合课程理念的要求，形成了一套有效的学习模式.

1.任英杰.促进学生“迷思概念”转变的POE策略及案例分析［J］.基础教育研究，2013（2）.

2.顾江鸿.预测—观察—解释——一种基于现代教育研究的演示策略［J］.教育科学研究，2009（5）.

3.赵国敏.概念转变教学中POE策略的探索和尝试［J］.数学教学，2014（4）.