小议中学生数学思维品质的培养

☉江苏省南通中学 张 勤

小议中学生数学思维品质的培养

☉江苏省南通中学 张 勤

数学教学的根本任务不仅在于向学生传授科学的知识，更重要的是在教学的过程中优化学生的思想品质，让学生从“学会”到“会学”，即掌握数学思维方法，发展思维品质，促使学生形成多种能力.

数学思维品质具有四个方面的特征：灵活性、创造性、批判性和发散性.这四个方面是衡量学生数学能力的基本标准，更是学生以后继续学习和踏上社会所必需的基本能力.这就为我们指明了在数学教学过程中培养学生能力的基本方向.

一、变式编题，培养思维的灵活性

数学思维的灵活性表现在对问题题设的整体把握的基础上灵活运用已有知识来解决问题的能力.

课本知识比较固定单一，所以我们的教学在基于课本的前提下，引导学生对问题进行深层次的剖析，可以根据自己的知识结构，建构新问题，激发学生的学习兴趣，同时也加强了学生思维灵活性的培养.

例如，一元二次不等式的恒成立问题是学生学习的难点，又是教学的重点.在课堂上先给出了一个相对简单的引例：

问题1 若对一切x∈R，不等式x2-2ax+2-a≥0恒成立，求a的范围.

引导学生分析，这个问题是开口向上的抛物线恒在x轴的上方，用数学语言描述：函数f（x）=x2-2ax+2-a，只要对应的判别式Δ≤0.鼓励学生结合自己的学习和自己平时练习的反思总结，进行变式编题，挖掘这类问题还可能出现的形式及解题方法，加强灵活性训练.

（1）二次项系数带字母：若对一切x∈R，不等式ax2-2ax+2-a≥0恒成立，求a的范围.

分析：①a=0，2≥0成立；②a＞0，如上Δ≤0；③a＜0，根据图形此时无解.

（2）函数定义域有限制条件：若对一切x≥-1，不等式x2-2ax+2-a≥0恒成立，求a的范围.

分析：①函数f（x）=x2-2ax+2-a与x轴没有公共点，即Δ＜0；

②函数f（x）=x2-2ax+2-a与x轴只有一个公共点，即Δ=0；

③函数f（x）=x2-2ax+2-a与x轴有两个公共点，即

其他还可以改变函数的定义域，x可以用sinx等函数代换，最后要总结些问题“万变不离其宗”，紧紧抓住函数在定义域上的单调性、最值，在解题的过程中要注意灵活运用分类讨论思想、数形结合思想、方程思想等.通过这样的自己变式编题，自己解决，对这类问题有了一种整体的理解，便于以后灵活的处理.

二、独辟蹊径，培养思维的创造性

数学思维的创造性是在数学思维活动中，通过思维运用新思想、新方法、新观点，揭示问题的本质.

问题2 已知函数f（x）是定义在［-1，1］上的奇函数，且（f1）=1，若a，b∈［-1，1］，a+b≠0，有

（1）证明f（x）在［-1，1］上的单调性；

（2）若f（x）≤m2-2am+1对所有x∈［-1，1］，a∈［-1，1］恒成立，求m的取值范围.

（1）是在已知区间上证明函数单调性，学生一般都会利用定义法证明该函数在［-1，1］上单调递增（为第（2）问作铺垫）.

（2）要使f（x）≤m2-2am+1对所有x∈［-1，1］，a∈［-1，1］恒成立，即m2-2am+1≥fmax，因为f（x）≤f（1）=1，所以m2-2am+1≥1，即m2-2am≥0，a∈［-1，1］.

按照一般的方法是进行变式用m表示a，再对a的范围进行讨论，得到m的范围，整个过程比较烦琐.引导学生是否能用其他的方法解决，比如函数思想：一次函数的保号性.

令g（a）=-2ma+m2≥0在［-1，1］上恒成立.

三、错题反思，培养思维的批判性

数学思维的批判性是在数学思维活动中思维严谨而不疏漏，能准确地辨别和判断，善于觅错、纠错，以批判的眼光观察事物和审视思维的活动，具有这种思维品质的学生，就会善于发现矛盾，一针见血地指出问题的症结，然后采取直接有效的途径，解决问题.

一方面，在教学中，我们可以引导学生对数学语言的细微差异的辨析.例如，在平面内任意一条直线都有倾斜角；在平面内任意一条直线都有斜率.在深刻理解斜率概念的基础上，敢于发现思维中的漏洞，并加以纠正.

另一方面，可以通过典型错误问题的分析，提高学生的辨析能力.

问题3已知f（x）=1+log2x（1≤x≤4），求g（x）=f2（x）+f（x2）的最值.

错解：因为f（x）=1+log2x，所以

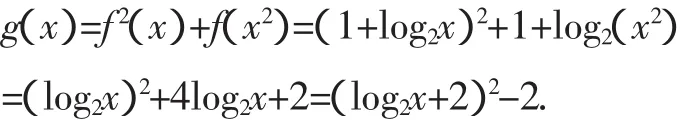
因为1≤x≤4，令log2x=t，t∈［0，2］，

所以g=（t+2）2-2在［0，2］上单调递增，所以当t=0时，有最小值，g（x）min=2；当t=2时，有最大值，g（x）max=14.

初见解题过程时，看似没问题.要引导学生在思考函数问题时，还是抓住函数的定义域等性质.再经过思考后，学生发现到g（x）=（1+log2x）2+1+log2x2，此时定义域已经改变为1≤x≤2，令log2x=t，t∈［0，1］，所以g=（t+2）2-2在［0，1］上单调递增，所以当t=0时，有最小值，g（x）min=2；当t=1时，有最大值，g（x）max=7.

在解题后的反思时，重现刚才的思维过程，注重隐含条件的运用，还可以引申到相关的方程、不等式中，注重此类情况的应用迁移.

数学思维品质的各个方面是相互联系、相互渗透，更是相互促进的.所以在数学教学过程中，要基于学生已有的数学水平和数学思维品质，根据数学问题的特征，启发、引导学生不断的尝试、探索，将各种思维品质在整个教学活动中有机地结合起来，这样才能更好地培养学生的数学思维品质，提高学生数学思维的层次.

四、多元探索，培养思维的发散性

思维品质的发散性，是数学教学亟需培养的一种品质.我们知道，发散性是思维比较具备启发的重要特性，对于学生后续的发展和数学素养的提高有着重要的作用.培养发散性最好的方式，是对问题进行多元探索，从不同角度解决问题去思考.

问题4 当a为何值时，不等式x2-ax+a+1＞0（x∈［0，1］）恒成立？

分析：对于本题学生往往以二次函数为根基进行初步探索，通过对图像的分析，发现该函数随着字母参数a的变换需要进行讨论，这属于分类思想的基本使用，是问题解决的一种基本方式；有些能力较强的学生则将问题通过变换主元的角度切入，通过变换主元，发现本题从一次函数入手，显得非常容易，利用函数图像解决；更有学生将问题分解为两个不同函数切入，从两个函数图像的角度思考，也不失为一种好方式；甚至有学生从纯粹的代数角度思考，将不等式的解集中，寻找问题解决的机会，尽管计算可能有些烦琐，但是理论角度而言是可行的，而且是直觉性思维的一种体现.

发散性1：令函数f（x）=x2-ax+a+1（0≤x≤1），则函数图像的对称轴为，然后分三种情况进行讨论，分别求出f（x）在各种情况下的最小值，只要使最小值大于0，即可求出a的取值范围.

发散性2：当x=1时，不等式对任意实数a都成立，此时a∈R.当x≠1时，不等式可转化为恒成立.只需求函数上的最大值ymax，使a＞ymax即可.故a的范围为（-1，+∞）.

发散性3：在同一坐标系下作出函数y1=x2和y2=a（x-1）-1（恒过定点（1，-1））的图像.要使y1＞y2在x∈［0，1］时恒成立，直线y2的斜率a应大于-1，故a∈（-1，+∞）.

发散性4：设原不等式的解集为A，则问题可化为：当a的取值范围为何时，［0，1］⊆A？当Δ=a2-4（a+1）＜0，即时，A=R，满足［0，1］⊆A；当Δ=时，不 等 式 的 解 集 A 为时，要使［0，1］⊆A，必须有或，解得-1＜a≤2-或

综上有a∈（-1，+∞）.

问题的解决使用了多元的探索，解决问题不仅仅是寻求问题的答案，而是通过不同的思考去寻找、对比更合适的问题的解决方法.有时我们对做过的题进行温故的时候，会发现其中所含的数学思想方法是非常具有典型性和代表性的，对这些思想方法的提炼、总结、归纳，提高学生思维的发散性，会给学生今后的解决问题以及思维品质带来较大的帮助.

1.苏小强.例谈数学教学中多解建构探索与思考［J］.数理化学习，2014（6）.

2.杨建辉.新课程标准下教师教学设计中应具备的几种意识［J］.数学通报，2011（2）.