新高考走班制下高二数学课堂有效教学的尝试——以“直线与椭圆的位置关系”为例

☉浙江省杭州市余杭实验中学 翟艳平

新高考走班制下高二数学课堂有效教学的尝试
——以“直线与椭圆的位置关系”为例

☉浙江省杭州市余杭实验中学 翟艳平

一、背景

2014年浙江高考改革新方案出台，文理不分科，采取七选三模式，语文、数学除外，其他科目均有两次考试机会.笔者所在学校是一所省二级特色普通高中，学生的数学基础比较薄弱，思维也比较缓慢，高中实施选课走班教学.分层走班教学第一次试行，学生一片忙碌，跑来跑去，教师心中一片茫然，不知何去何从.2016年12月17日，中国教育学会第二十九次学术年会期间，“数学核心素养与高中数学教学质量”的分论坛在成都举行，会上章建跃等提出让数学核心素养落地生根.

二、精准定位教学目标让课堂动起来

教育教学的主阵地在课堂，如何有效合理利用课堂40分钟尤为重要.张金良老师在浙江省高中数学新课程实施方略中提到：课堂教学的有效性是指通过课堂教学活动，学生在学业上有收获、有提高、有进步.每节课都应该让学生有实实在在的认知收获和或多或少的生命感悟.针对本校学生的生源特点，再结合本班学生的实际情况，我精准教学内容，每堂课确定一个小目标，力求所选题目适合学生，部分题目学生跳一跳也能够得着，充分接近学生的最近发展区，让学生充分接受并掌握本节课的教学内容.因为笔者面临的是中等甚至中等偏下的学生，教学中经常向学生重点强调“会，就保证对”，一定要减少“会而不对”的题目的数目.每一张练习卷下来都要学生总结“会而不对”的题量，有多少，并逐一分析原因，在平时的训练中如何避免，下一次的测试中要保证减少.下面就以“直线与椭圆的位置关系（第一课时）”一课为例，来谈谈自己的粗浅体会，和同行交流.

三、教学过程实录

（一）例题选择

人教版选修2-1（下称本教材）第48页练习：6.求下列直线和椭圆的交点坐标：

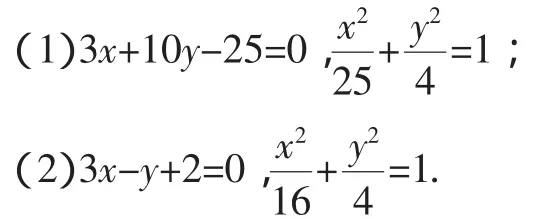
选题意图：通过运算理解直线与椭圆的位置关系，进一步归纳总结并推出弦长公式.属于基础题，要求人人“会就对！”

这个题目学生都会做，关键是能否做对，课堂中我让学生选一道我来演算，另外一题他们做.然后我随机选了一个学生的正确过程进行实物投影，接着让各班当天课代表统计正确率：1班，6/6；2班，6/7；3班，5/5；4班，6/8；5班，7/9；6班，5/7.从中可以看出，部分学生的计算堪忧，不过通过班级与班级之间的对比，学生兴致高涨，斗志昂扬，尤其是二班那个错了的同学说自己是一时失误，接下来再比.在梳理了直线与椭圆的位置关系并推导出弦长公式后，马上进行变式训练.

（二）变式练习

选题意图：本题主要考查直线与曲线相交的弦长公式的应用.通过学生不同解法突出弦长公式快速简便的优越性.属于圆锥曲线问题的基础题.要求人人“会就对！”

2.（2014学年杭州市统考高二数学第19题）F1，F2是椭圆的左，右焦点，过F2的直线AB交椭圆于A，B两点，且满足三角形F1AB的周长为8，又椭圆的离心率

（1）求椭圆C的方程；

（2）若直线l过点（0，2），且与椭圆相切，求直线l的方程.

选题意图：本题主要考查了由椭圆的性质求解椭圆方程，直线与曲线位置关系的判断.通过统考题目让学生深刻意识到运算准确的重要性，确保“会就对！”

图1

（1）当直线l过椭圆右焦点时，求线段CD的长；

选题意图：本题主要考查了由椭圆的性质求解椭圆方程，直线与曲线相交的弦长公式的应用及向量的数量积的坐标表示的应用，属于圆锥曲线问题的综合应用.

因为是初始训练，所以我和学生们一起分析了解题思路，过程如下：

师：如何选取数量积公式？为什么？

生：坐标表示，因为夹角不知道.

师：非常好！那么问题来了，x1x2，y1y2怎么求啊？

学生沉默，教室一片寂静.

师：能不能像求弦长公式，联立方程，设而不求？

生：好像不行，P，Q不在椭圆上.

师：那只能求出P，Q的坐标了.

生：啊？！

师：试试看能不能求，先说说怎样求？

生：那好吧.

生1：点P是直线l与x轴的交点.

师：非常好！那么点Q呢？

学生沉默，教室一片寂静.

师：来再一次读题，（停顿）点Q怎么得来的？

生：直线AC与直线BD的交点.哦，求两条直线的交点.可是直线BD方程不知道啊.

师：不知道可以求啊.

生：怎么求？B点坐标知道，只要求出D点坐标，怎么求呢？

师：（笑着说）很好啊，看看你们自问自答，自己都一步步分析出来了，请继续！

生：D点是与椭圆的另一个交点.天啊，要联立方程求解，这好麻烦！

师：太棒了！都说出来了，不要嫌麻烦，至少你们说的都是对的，要是都说不上来了那就算了.好，来咱们挽起袖子，拿起笔，沉下心来先算D点坐标.算不出来，咱们今天饭都不要吃了.

就这样，第二问就在磕磕绊绊中求出来了，学生还是觉得非常有成就感，至少面对这类问题，迈出了敢做敢动手的第一步.最后我鼓励学生单凭兴趣，没有坚持不懈、日积月累是学不好数学的，当你费尽心机、满头大汗解出一道你认为的难题，当你尝尽为求解而奋斗的酸甜苦辣时，就为你的人生积累了一笔宝贵的财富！

四、教学启示与反思

1.精心选题，让学生在课堂上动起来

一堂数学课40分钟，笔者一共选取了4个题目，所选题目带上明确强烈的训练意图和思维标志.主要通过运算、推理的训练，培养学生的逻辑思维能力；通过题目层层递进，让学生觉得跳一跳就够得着，要在他们脑海中留下最重要的东西：理性分析，精准运算.

这其中笔者有亲自演算，有循循善诱的点拨，而其他题目就用课堂时间让学生充分完整演算.即便如此，通过各班课代表的统计，我们学生的运算并不尽如人意，计算错误，速度缓慢…最后一题综合题的第二问，适度增加难度，磨炼学生的意志力.整节课中，学生除最开始看我运算外，基本没有停下来，除了在思考，一直在计算.在此过程中，学生收获的是信心.

2.让课堂外的情感因素延伸到课堂

笔者所带的两个班级的学生来自于6个班，每个班6～7人，他们分散在不同的班级，这为课后的数学学习管理带来极大的不便.为了便于管理，我推行了课代表轮流制：每天每班一人，课代表的作业要求当天完成并面批，他就是当天课后的小老师，其他同学作业上有问题都去找他解决，第二天上交作业时以便条的形式反映其他同学的作业情况.这样每天都有十二名学生面对面和我交流，不仅帮助学生解学习之困，更架起师生的情感之桥，只有“亲其师”，才能“信其道”“笃其行”，而且最重要的通过“小老师”制，极大地调动了学生学习数学的积极性.课余时间，在教室经常看到学生三五成群讨论数学题目，有时他们为了一个题目争得面红耳赤，一直闹到我这里.在其他老师羡慕的眼光中数学学习这样就实现了学生的自主管理，学习积极性空前高涨.尤为重要的，在我的课堂中，学生没有开小差的，好歹也要给点面子，学生给力，紧随老师步伐，课堂自然效率高.