由一道行程问题谈问题解决中逻辑思维的形成

☉浙江省平湖中学 毛良忠

由一道行程问题谈问题解决中逻辑思维的形成

☉浙江省平湖中学 毛良忠

用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达现实世界，这是数学素养的一种体现.学会数学地思考问题并解决问题是数学教学的目标之一，课堂教学中应重视培养学生的数学思维，让问题解决更具逻辑性.

在平时教学中，我们总会遇到一些好问的学生，他们提出的问题有些往往不是我们教师十分熟悉的，教师在解答中也经常卡壳.在帮助指导学生解题的过程中，我们应该更多地向学生传授自己是如何走出困境，如何优化解题过程，多引导好念头，良好的逻辑思维是怎样形成的，也就是要教会如何思考问题的.下面的教学案例就是一次高一学生课外活动交流时的解题思维形成的呈现.

情境问题：若湖岸MN为一直线，现有一小船自岸边的A点沿与湖岸成α=15°角方向匀速向湖中驶去.有一个人自A点同时出发，他先沿岸走一段再入水中游泳去追船.已知人在岸上走的速度为v1=4m/s，在水中游泳的速度为v2=2m/s，试求船速至多为多大时此人才能追上小船.

这是源于生活的一道应用题，它很好地考查了学生的思维能力及数学运用意识.学生最初的感觉就是可以借助刚学过的解三角形知识来求解.

初探：设船速为vm/s，小船出发后t时被人追上，则船的行程为s=vt=AB.又设人在岸上走用时为t1，则人在岸上的行程为s1=v1·t1=4t1=AC，设人在湖中游泳用时为t2，则人在湖中的行程为s2=v2t2=2t2=BC，其中t1+t2=t.如图1，在△ABC中，由余弦定理知，|BC|2=|AC|2+|AB|2-2|AC·||AB|cosα，代入得8cos15°tt1v.接下来如何运算呢？几位同学都在这里卡住了，有同学将t1+t2=t代入消去t或t1，因运算量大且看不出问题的突破口而败下阵来.一段时间后有同学想到了方程两边同除以t2，得到，令=k，则方程整理得4（1-k）2=16k2+v2-8cos15°kv.再将它整理成关于k的二次方程12k2+8（1-cos15°v）k+v2-4=0，要使k存在，则Δ=［8（1-cos15°v）］2-4×12（v2-4）≥0，即，解得或v≥（舍），于是小船的最大速度为

图1

上面的成功求解在于发现了原方程恰是含t的齐次式，灵巧的换元使问题走向成功.能不能将上面的过程进一步优化呢？上面一波三折的处理促使我们思考有没有更好的方法引领思维走向更成熟.

优化：设船速为vm/s，船出发后经时间t被人追上，则船的行程为s=vt=AB.又设人在岸上走用时为kt，则人在岸上的行程为s1=v1·kt=AC，人在湖中游泳用时为（1-k）t（0＜k＜1），则人在湖中的行程为s2=v2·（1-k）t=BC.考虑到v1=2v2，在△ABC中，由余弦定理知，|BC|2=|AC|2+|AB|2-2|AC|·|AB|cosα，代入得［v2（1-k）］2=（2v2k）2+v2-4v2vkcos15°，令，化简得到关于k的二次方程3k2+（2-4cos15°x）k+（x2-1）=0，由题知k存在，故Δ=（2-4cos15°x）2-4×3（x2-1）≥0，即（4cos215°-3）x2-4cos15°x+4≥0，即，解得或（舍）.所以

上面的求解让我们看到了从不同的角度设元能简化运算，同时利用速度间的倍数关系化多元为少元，简化后的表达式让我们更清楚地看到了量之间的内在关系.

仔细观察上面的三个量s=vt=AB，s1=2v2·kt=AC，s2=v2·（1-k）t=BC之间的联系，我们也可将此问题适当转化并抽象成一个更简洁的数学问题：已知△ABC中，AB=x，AC=2k，BC=1-k，∠BAC=15°，求x的最大值.

对于这样一个问题的提出，学生都感觉非常亲切.模仿上面的过程可直接求解.有没有其他的求解方法呢？能不能从“形”的角度进一步思考呢？已知条件中的AC=2k，BC=1-k，给了我们更多的思维想象空间.

在MN的异侧过A作射线AH，使∠CAH=30°，过C作CH垂直于AH，垂足为H.则有，由于BC+CH=1（定值），易得B，C，H共线时AB最大（如图2，当H1C1+C1B1=BH=1时，AB1＜AB），此时∠ACH=∠BCN=60°，显然此时△ABH为等腰直角三角形.如果我们将AB还原到实际问题中，即，于是

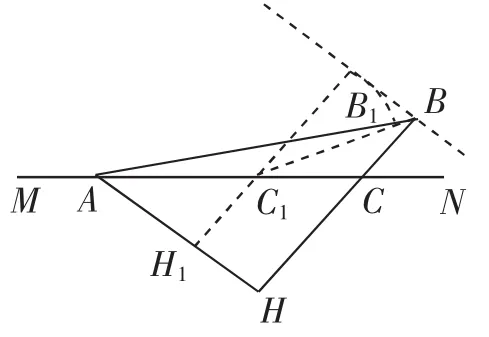
图2

巧解2：考虑到AC+2BC=2（定值），于是在直线MN上构造CP=2BC，则AP=AC+CP=2.于是问题转化为定线段AP上确定一个点C，使得射线AQ上的点B满足且|AB|达到最大值.

图3

由上面的探究过程我们可以进一步地通过简洁的几何作图寻得人在岸上入水游的最佳点C及船速最大时的相遇点B.

几何做法：在定线段AP上，过点P作直线BP使得∠APB=30°，交射线AQ与点B，过点B作BC⊥BP，交AP于点C.则C就是入水点，B就是船速最大时的相遇点.

下面我们计算此时AB的数值.如图4，在△ABP中，易得AP=2，∠APB=30°，∠ABP=135°.由正弦定理得计算得.同时由AB量的实际意义知，于是

图4

上面两种方法我们充分享受了数学模型的强大力量，感受了巧解并不是“帽子里掏出来的兔子”，而是对问题本质理解后的思维再创造.观察上面的两种解法我们欣喜地发现问题，求解中都出现了一个关键的量∠BCN=60°，它又有怎样的内涵呢？

思维的深化：如图5，设人在C点入水并在B点刚好能追上小船.这表示此时人追上小船所用时间最少，对应的小船速度最大，现设D，E是C点两侧附近无限靠近C点的两个点，并设从D，E点入水追小船所用的总时间相等.现在BD上截取BF=BE，当BD，BE无限接近于BC时∠BFE接近于90°.由于从D，E点入水追小船的所用的总时间相等，所以人在走DE段与在水中游DF段所用时间相等.于是，所以，所以∠FDE=60°.因为D，E无限靠近C，所以∠BCP=60°.作BP⊥BC交MN于点P，于是CP=2BC，也就是人游BC段与走CP段所用的时间相等.所以人自出发点A经C点再到B点与人在岸上走AP所用的时间相等，并都等于小船从A到B所用的时间，即.在△ABP中，由，故

图5

由此我们用逼近思想（微元法）破译了巧解中的一个关键角∠BCN=60°.

回顾上面的问题探究过程，我们从最初的生活实际问题出发，在充分理解了问题的要义后，通过代数运算我们找到了小船的最大速度值，同时在求简优化思想的引领下，我们将实际问题抽象提炼成了一个易于理解的几何最值问题（它其实就是用数学语言描述实际问题的一个过程）.同时几何作图让我们清楚地发现了一个特殊的角∠BCN=60°，微元法的探求让形更具“理性”（这些过程也就是用数学的眼光观察问题，用数学的思维分析问题的过程）.在问题的探究过程中更多地呈现了怎样想问题，好的解题思维是怎样形成的.

更一般地：若人在岸上走的速度为v0，在水中游泳速度为mv0（0＜m＜1），试求船速为多少时此人才能追上船.

如图6，在MN上任取两点P、C，作以C为圆心，m|CP|为半径的圆，再过P作圆C的切线交射线AQ于点B，则点B就是船速最大时人入水后与小船的相遇点.其中sin∠BPC=m，由正弦定理知.故船速至多为

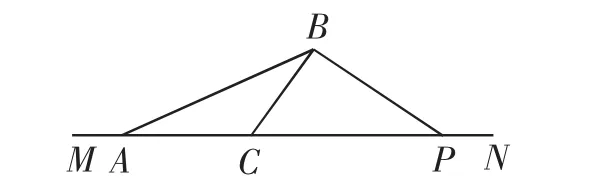
图6

数学是研究数量关系和空间形式的科学，数学知识本身的规律性以及知识之间的逻辑关系是客观存在的.在教学中我们要营造学习探究的氛围，挖掘数学信息，从不同的观点、不同的角度去审视问题，去揭示问题蕴含的本质.课堂教学要明确教学的着眼点在哪里，不能就是为了解题而解题，要关注学生的思维活动，要教学生如何看问题，如何开展思维活动.要用联系的观点认识学科知识之间的逻辑联系，缺乏教学逻辑的教学常常表现在所研究的问题是孤立的，不能揭示出问题之间的逻辑关系.在教学中我们希望通过典型问题的研究帮助学生在理解数学问题和研究数学问题的过程中，感悟到数学知识的内在的逻辑性，关注思维逻辑的形成过程，让学生体味“好念头”“好解法”，自己也可以这样发现.

只有教给学生的东西是赋有逻辑的、本质的，学生才能受益.只有教师从逻辑上明白了自己所教授的数学知识，才能教给学生真正的有意义的数学，才能让学生体味数学是有用的，是自己能亲身体验习得的.

1.任念兵.浅谈物理素材在数学教学中的作用［J］.数学教学，2006（4）.

2.蔡凯彬.从一道题看物理所涉及的解题方法与技巧［J］.中学物理，2010（11）.

3.张鹤.数学教学的逻辑——基于数学本质的分析［J］.北京：首都师范大学出版社，2016（10）.F