数据结构中的动感形态研究与应用实践

刘华敏

（安徽文达信息工程学院计算机工程学院 安徽 合肥 231201）

数据结构中的动感形态研究与应用实践

刘华敏

（安徽文达信息工程学院计算机工程学院 安徽 合肥 231201）

《数据结构》是计算机专业的一门重要的专业核心课程，在教学的过程中引入实例、动画和图形等多媒体方式，让学生对教学内容有较直观的理解。在理论与实践结合的教学环节，引用图论中广度优先搜索的思想，求解公交查询系统中获取“最优”换乘路线问题，从理论上升到实践，提高学生解决实际问题的能力。

多媒体；广度优先搜索；最短路径

1.数据结构中的动感形态研究

1.1 多媒体方式的应用

数据结构的内容比较抽象，学生在学习时愿意花费时间和精力去学。但大部分学生往往感到在学的过程中力不从心。上课时老师讲解的知识点能理解，下课后自己无法能灵活运用所学的知识完成老师布置的实验作业和解决与实际相关的问题。为了解决在数据结构的教学中普遍存在的这个问题，要求老师在教学过程中为学生建立一个动静交互的教学环境，开阔学生的视野，丰富学生的想象力，调动学生的学习兴趣，从而大大提高课堂教学效率[1]。

在教学中，老师的课件要真正的引入多媒体技术即融入图像、动画、、文本等内容，使其成为一个具有直观性和交互性的课件。著名教育心理学家梅耶(Richard E.Mayer)的研究和实验表明，多媒体有下面2个优点：

(1)多媒体性：多表征方式优于单表征方式。

(2)邻近效应：言语信息与视觉信息结合呈现优于分离呈现。多个元素完美的结合真实的演示了算法执行的过程，可产生1+1〉2的协同效应，抽象算法用形象的、动态的直观图表示，让人容易理解和接受[2]。如讲到顺序队列入队和出队时，演示这样的动画过程如图1所示。

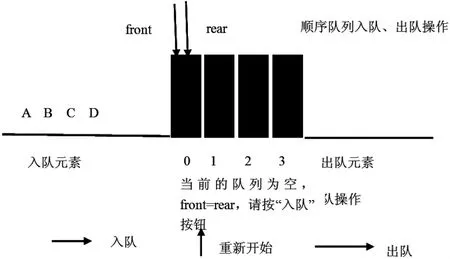
图1 顺序队列入队、出队操作

动画具有动静结合、图文并茂的特点，动画的演示逼真的展现了队列入队和出队的过程，从平面走向三维，从抽象走向直观，较好的抓住学生的眼球，集中注意力观察这一过程，更好的理解队列入队和出队的算法思想。

1.2 色彩元素的渗入

现在的教学离不开计算机辅助教学手段的支持，以存储容量大、教师授课进度快等特点著称，这就对教师的课件质量提出了新的要求。色彩在各个领域扮演的角色和表现形式、手法、目的有所不同，但色彩对物的表现所追求的和谐之美却是一致的。因此，配色部分对于制作数据结构课件的人而言无疑是新的挑战。

针对数据结构内容抽象、信息容量大、知识点复杂等方面，在课件的制作过程中根据不同的内容选用不同的色彩。

数据结构内容简单、易懂的部分，可以选用振奋人心、精神焕发的色彩配色。例如讲到队列的入队和出队的基本操作时，以选择红色或橙色系列作为文字的底色，在暖色系的视觉中轻易获取知识点，激发学生学习的兴趣。讲到树、森林遍历的相关内容时，可以插入一颗枝繁叶茂的大树和一片绿树成荫的森林，配绿色底纹的文字说明树的遍历和森林的遍历，转换等问题，首先让学生在视觉的图画中放松心情，产生愉悦的心理；然后在宁静、能慰藉心灵的色彩中汲取难懂深奥的算法，在祥和的状态中思考问题，发挥人的思维，积极开动脑筋，主动学习。

2.图在公交最优路线查询系统中的应用

最近几年，城市公交系统发展速度惊人，市民的出行更加便捷。然而，随着路线的增加，市民在出行时会综合考虑各种因素选择出行路线。如何在公交问路查询系统中，根据出行者的实际需要获取“最优”换乘路线？要解决这样的一个问题，就需要用到《数据结构》中的有向图的相关知识。

首先对给定公交线路构成有向路网，然后将该问题的求解归结到求单源最短路径。如果将公交查询系统中的各种“最优”等价为图中的“最短”，这个问题就迎刃而解了。

2.1 图的表示和术语

图由一个顶点(vertex)的有穷非空集V(G)和一个弧(arc)的集合E (G)组成，通常记作G=(V,E)。有序对〈v,w〉表示从v到w的一条弧(arc)，若弧有方向性，通常用一带方向箭头的线段表示，即v(没有箭头的出发端)为弧尾，w(带箭头的结束端)为弧头，此时的图称为有向图。无序对(v,w)表示从v到w的一条弧，同时存在w到v的一条弧，此时的图称为无向图。

在实际应用中，图的弧或边往往与具有一定意义的数相关，称这些数为“权”。如图2所示：

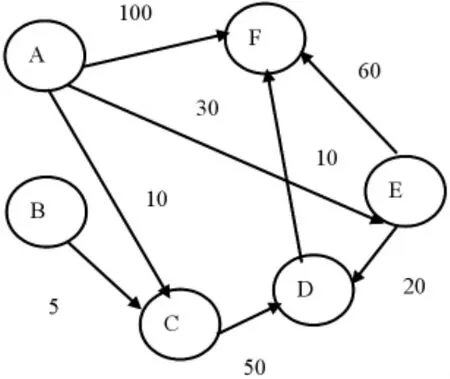
图2 带权有向图G

若有向图G中n+1个顶点直接都有弧存在（即〈v0,v1〉,〈v1,v2〉,....,〈vn-1,vn〉是图 G中的弧)，则这个顶点的序列{v0,v1,...vn}为从顶点 v0到顶点vn的一条有向路径，路径中弧的数目定义为路径长度。若序列中的顶点都不相同，则为简单路径。

2.2 图的存储结构

(1)邻接矩阵。

邻接矩阵是用于描述图中顶点之间关系（及弧或边的权）的矩阵，假设图中顶点数为n,则邻接矩阵A=(ai,j)n*n定义为：

在网的邻接矩阵的表示中，若Vi和Vj有弧相邻接时，ai,j的值应为该弧上的权值，否则为∞。

(2)邻接表。

邻接表是图的一种链式存储表示方法。在有向图的邻接表中，从同一顶点出发的弧链接在同一链表中，邻接表中的结点的个数恰为图中弧的数目。

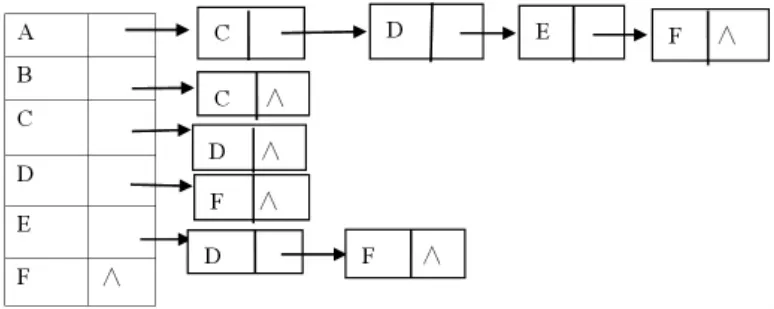
图3 图G的领接表

2.3 图的遍历

图的遍历有2种搜素路径：深度优先搜索和广度优先搜索。

(1)深度优先搜索：假设图G中所有的顶点原始状态都是没有访问的，则选择某个顶点作为起点，首先访问该起点，然后按照深度优先遍历的思想，依次访问与它相连的各个未被访问的邻接点，直至图中所有和起点有路径相连的顶点都被访问过。如果此时图G中还存在其他顶点没被访问，则另选一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问结束。

(2)广度优先搜索：假设图G中所有的顶点原始状态都是没有访问的，则选择某个顶点作为起点，首先访问该起点，由近至远，依次访问和起点有路径相通的未被访问的顶点。如果此时图中还存在其他顶点没被访问，则另选一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问结束。

3.最短路径的求解

如果在计算机上建立一个公交咨询系统，可采用图或网的结构表示实际的交通网络。在公交咨询系统中，出发点A与终点B之间存在的路径可能有三种情况：①没有路径；②存在唯一的一条路径；③存在多条路径。如何求得出发点A与终点B之间的最短路径，此时应分析公交线路构成的有向路网，根据“较快捷”、“少步行”及“少换乘”等赋不同的权值，利用迪杰斯特拉（Dijkstra)算法求解从源点A到终点的最短路径。

3.1 迪杰斯特拉（Dijkstra)算法

迪杰斯特拉（Dijkstra)提出了一个按路径权值长度递增的次序产生最短路径的算法，具体描述如下：

(1)假设用带权的邻接矩阵arcs[n][n]来表示带权有向图，arcs[i][j]表示弧〈vi,vj〉上的权值，若〈vi,vj〉不存在，则置arcs[i][j]为∞。S为已找到从v出发的最短路径的终点的集合，它的初始状态为空集[3]。那么从v出发到图上其余各定点vi可能到达D[i]=arcs[Locate Vex(G,v)[i] vi∈V。

(2)选择vj，使得D[j]=Min{D[i]|vi∈V-S}，vj就是当前求得的一条从v出发的最短路径的终点。令 S=S∪{j}。

(3)修改从v出发到集合V-S上任一顶点vk可达的最短路径长度。如果D[j]+arcs[j]k]〈D[k]，则修改D[k]为D[k]=D[j]+arcs[j]k]。

(4)重复(2)(3)共n-1次，由此求得从v到图上其余各顶点的最短路径是依路径长度递增的序列。

3.2 有向图G求解的具体过程

带权的有向图G(图2)中从A到其余各顶点之间的最短路径。

(1)G的带权邻接矩阵表示如下：

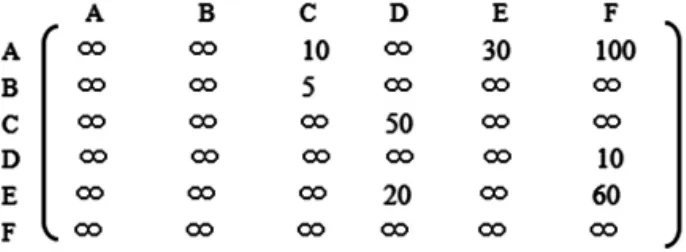
图4 G的带权邻接矩阵

(2)若对G运用迪杰斯特拉（Dijkstra)算法，则所得从A到其余各顶点的最短路径，以及运算过程中变化的D向量情况，如表1所示：

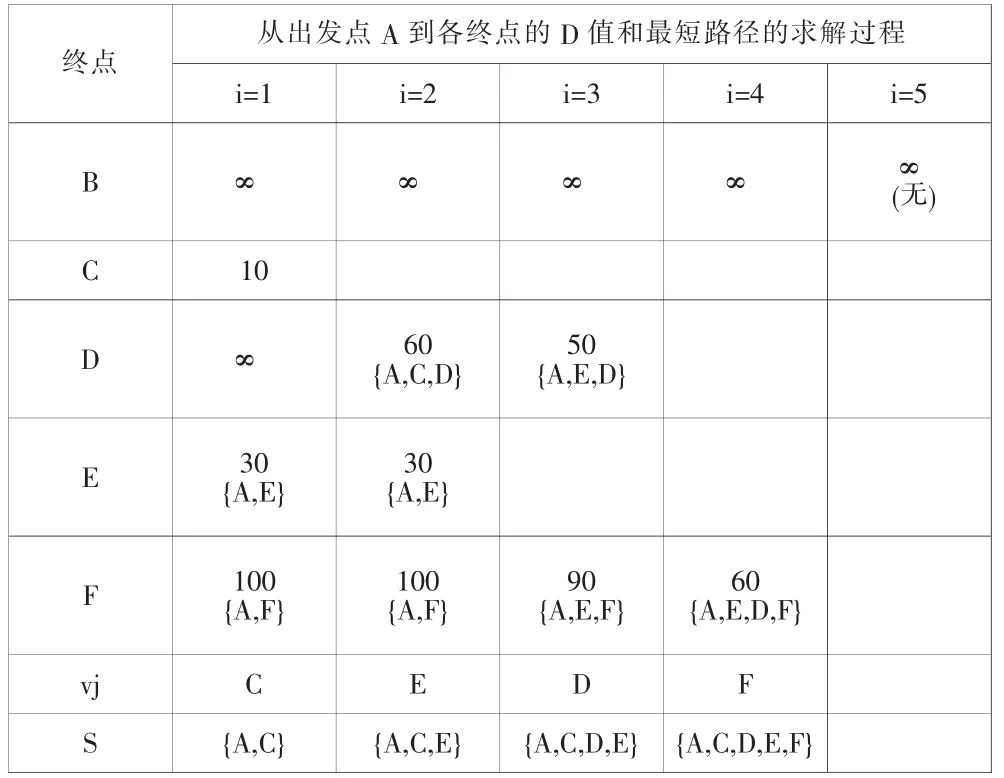
表1 D向量变化情况

从表1，我们能直观的了解到图G中顶点A到其他所有顶点的最短距离A→B=∞，A→C=10，A→D=50等。根据运算结果绘制的SPF树如图5所示：

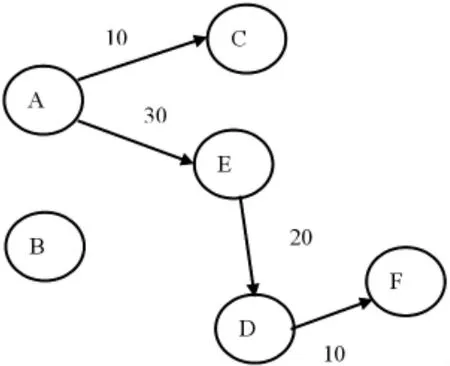
图5 有向图G的SPF树

4.结束语

算法的发展与应用是密不可分的，但在学习《数据结构》的过程中，运用动静结合的教学方法讲授教学内容，将算法与实际问题相结合，能灵活的调动学生学习的主动性，激发学生探求新知识的兴趣，拓展学生创新能力的培养。以Dijkstra算法为基础，求解单源最短路径的实际问题，将学生的理论知识运用到实践中。随着公交线路查询系统的功能不断的完善，实时最优路径的求解是亟需解决的，Dijkstra算法也会不断的被改进。

［1］张伟.数据结构算法设计题的测试程序辅助构建研究[D].广东：广东工业大学，2012.

［2］张建伟，孙燕青.多媒体与网络学习的心理机制[J].外语电化教学，2004，(4).

［3］严蔚敏等编.数据结构[M].北京：清华大学出版社，2004.

T-01

A

2095-7327（2017）-08-0161-02

安徽省省级质量工程教学研究重点项目“基于项目和实践技能的应用型本科《数据结构》课程教学改革研究”研究成果，项目编号为2014jyxm427。

刘华敏（1978—），女，安徽安庆人，安徽文达信息工程学院讲师，研究方向为数据挖掘、程序设计和网页设计。