高中数学中奇偶函数的图象特征

◆段美伊

高中数学中奇偶函数的图象特征

◆段美伊

周期性、奇偶性、连续性等都是函数学习当中学生应该掌握的知识点。其中，奇偶性是函数性质当中重要的组成部分，函数奇偶性是对函数概念以及相关知识点的深化和发展，对学生的理解能力以及逻辑思维能力提出了很高的要求。学生在学习函数奇偶性的过程中，应该重点掌握奇偶性的性质、定义、图像的特征等，只有这样才能做到有的放矢，进而实施有针对性的学习方法，提高学生的数学成绩。本文主要对奇偶函数的特点进行了分析，并通过相关例题的解答，加深学生对对奇偶函数的理解，以此使高中学生全面掌握对奇偶函数相关知识点。

函数；奇偶性；定义域；图像

一、奇偶函数定义的认识

（一）抽象化的认识。函数奇偶性是对函数概念以及相关知识点的深化和发展，对学生的理解能力以及逻辑思维能力提出了很高的要求。在函数单调性的基础之上学习函数的奇偶性，学生能够将相关的知识最大程度联系起来，提高学习的效率。在函数奇偶性的学习当中，学生应该意识到函数奇偶性和函数的单调性一样，不是客观存在的，而是相关的数学教育工作者通过大量的函数关系式的研究，从结论当中抽象的概括出来的。同时对于函数奇偶性进行全面掌握，可以为后续关于函数知识的学习打下坚实的基础，在对函数的奇偶性进行抽象学习以及思考的过程中，不仅要对函数奇偶性本身所具有的性质进行学习和掌握，同时还要对解题过程中涉及到的思维以及问题进行抽象化的思考。所以，学生在学习函数的时候，首先就要意识到函数具有较强的抽象性。

（二）形式化的认识。在对函数奇偶性进行定义的时候，数学符号不能直接反映文字的内涵和观点，数学符号蕴含的是一种逻辑思维过程，在对函数奇偶性进行定义的时候，应该对其有一个抽象化的认识。比如f（x）、f(-x)、-f（x）都是对逻辑思维进行的一种本质的反映。这些数学符号，能够直观反映出函数关系式的特点以及性质。都有一个任意的点x在定义域内，对偶函数判断的方法就是f(-x)=f（x），对奇函数的判断方法就是f(-x)=-f（x）。

（三）数形结合的认识。在函数的学习过程当中，用来表达函数奇偶性的方式有很多种，不仅仅可以用文字语言对函数的关系式进行表达，同时还可以用符号，图形来对函数的关系式进行描述。所以，学生在学习函数奇偶性的过程当中，不仅仅能够解决函数奇偶性的判断，画出函数奇偶性的图像。同时对于数形结合的函数题目也要运用相关的知识进行灵活处理，只有将数与形充分结合起来，才能全面掌握函数的规律以及解题的思路和技巧。

二、奇偶函数的图像特征

在函数的关系式当中，对于奇偶性函数的图像特征的描述是：奇函数的图像是在坐标原点上对称的，偶函数的图像是关于坐标y轴对称的。比如可以设f（x）为奇函数，同时还可以设f（x）的奇函数和f（x）的图像是在原点对称的，那么就会得出：（x，y）→（-x，-y）。因为在某一个区间上，偶函数是单调递增的，所以它在对称区间上则是单调递减的，奇函数是单调递增的，所以它在对称区间上也是单调递增的。在这里需要指出的是：（1）不管是奇、偶函数，它的定义域首先要对称，定义域不对称就没有奇偶性可言，但是函数不一定是对称的；（2）奇函数定满足：f(-x)=-f(x)，偶函数定满足：f(-x)=f(x) ；（3）在图像方面，若奇函数的定义域是R，那么就可以得出f(0)=0。

三、关于函数奇偶性的具体应用

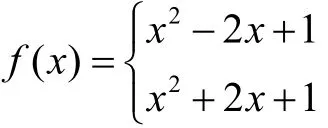
图1

结束语

奇偶函数在高中数学中是一个非常重要的知识点，学生学习起来有一定难度，这种函数和图像具有极其紧密的联系。在学习的过程中，一定要加强对基础概念、解题方法和图像特征的研究学习，掌握更加全面的知识，提升自身奇偶函数的掌握水平。

[1]张海燕.高中函数解题教学的研究[D].湖南师范大学,2012.

（作者单位：湖南师范大学附属中学）