高中数学中函数的单调性

◆郝子昱

高中数学中函数的单调性

◆郝子昱

函数是高中数学中的重点，同时也是难点，在高考的过程中占据了大量的分值。函数单调性相关的知识点通常是和高中数学当中的各个知识点联系在一起的，比如不等式、方程以及实际问题求解等，通过函数单调性的定义以及使用特点，求出函数关系式。学生只有充分了解和掌握函数单调性的定义和具体运用，才能在考试的过程中取得较好的成绩。本文主要对函数单调性的特点进行了分析，并通过相关例题的解答，加深学生对函数单调性的理解，以此使高中学生全面掌握函数单调性相关知识点。

数学 函数 单调性

一、对函数单调性的基本性进行分析

对于函数单调性的基本性质进行分析，主要从以下几个方面来进行分析。

第一就是如果在区间D上，f（x）和-f（（x）的单调性相反，那么就可以说如果f（x）在区间D上是增函数，那么-f（（x）在区间A上就是减函数。或者说如果f（x）在区间D上是减函数，那么-f（（x）在区间A上就是增函数。

第二就是在函数的关系式当中，f（x）和f（x）+C在区间A上的单调性是相同的。

第三就是在函数关系式当中，如果a〉0，那么就可以得出f（x）和af（x）在区间A上的单调性是相同的，如果a〈0，那么就可以得出f（x）和af（x）在区间D上的单调性是相反的。

第四就是如果f（x）和g（x）在同一个区间上都是增函数的时候，将f（x）与g（x）相加，得到的函数也是增函数，如果f（x）和g（x）在同一个区间上都是减函数的时候，将f（x）与g（x）相减，得到的函数无法进行判断。

第五就是如果f（x）和g（x）都是增函数的时候，而且f（x）和g（x）都恒大于零，那么f（x）g（x）也就是增函数，如果f（x）和g（x）都恒小于零，那么f（x）g（x）是减函数；如果f（x）和g（x）都是减函数的时候，而且f（x）和g（x）都恒大于零，那么f（x）g（x）也就是减函数，如果f（x）和g（x）都恒小于零，那么f（x）g（x）是增函数。

二、如何判断函数的单调性

定义法。在用定义法进行函数单调性的证明的时候，可以按照以下的步骤进行：第一就是在区间D上任意取x1、x2，同时令x1〈x2。第二就是做出f（x1）与f（x2）的差，即f（x1）-f（x2）。第三就是将f（x1）-f（x2）进行变形，常用的方法有因式分解、有理化、通分等。第四就是确定f（x1）-f（x2）的符号。第五就是根据“同增异减”的原则，对f（x1）-f（x2）在区间的单调性进行分析，得出结论。

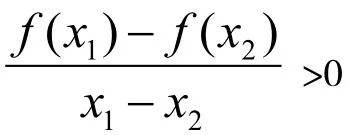
三、函数单调性在高中数学当中的具体应用

（一）确定取值范围。函数f（x）=-2x22+bx+c在x=1的时候有最大值1,0〈m〈n，并且当的时候，函数f（x）的取值范围为，求出m，n的值。

结束语

本文主要对函数单调性的特点进行了分析，并通过相关例题的解答，加深了学生对函数单调性的理解。学生要想学好函数单调性以及相关的知识，需要对相关的知识点进行全面的掌握，同时通过大量习题的练习，熟悉题目的规律，提高解题的思路和技巧，在养成良好的学习习惯的同时，在最大程度上提高数学成绩。

[1]董慧莉.高中生对函数单调性的理解水平研究[D].新疆师范大学,2016.

（作者单位：湖南省长沙市第一中学）