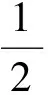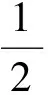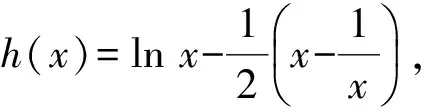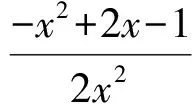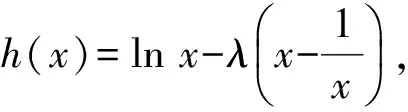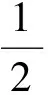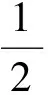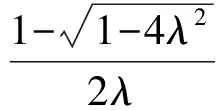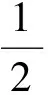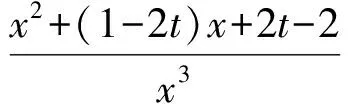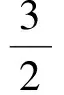拨开云雾见天日 守得云开见月明
——谈“f(x)·ln x”问题的一类简化算法
●王 强 (常州市第二中学,江苏 常州 213003)
拨开云雾见天日 守得云开见月明
——谈“f(x)·ln x”问题的一类简化算法
●王 强
(常州市第二中学,江苏 常州 213003)
高三数学模考中经常出现“f(x)·lnx”这类函数,如果先将lnx孤立出来,“拨去云雾f(x)”,往往只要求导一次,可避免多次求导,而且在后续的解题中也能减少讨论,终能“见月明”(解出题目),这个算法极大地减少了运算量.
孤立;求导;算法
新修订的《江苏省高中数学课程标准》提出:数学核心素养是数学课程目标的集中体现,是具有数学基本特征、适应个人终身发展和社会发展需要的必备品格与关键能力,是数学课程目标的集中体现.它是在数学学习的过程中逐步形成的.数学核心素养包括:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.数学运算是六大核心素养之一,是指在明晰运算对象的基础上,依据运算法则解决数学问题,具体体现在理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果[1].
1 问题由来,算法对比
笔者认为,运算能力的培养关键在于在做题中“学”和“悟”.为此,针对一些运算较为复杂的问题,我们应全方位地选择运算方法,在各种方法中“学”和“悟”其中的算理,运算能力提升才能得到有效的落实.2017年江苏省苏锡常镇一模试卷的第19题第2)小题满分为10分,平均分只有1.94分,得分率很低,错误的原因主要是大部分学生不能将lnx前的函数式“剥离”出来,而是采取直接求导的算法,因为涉及到二次求导,运算难度增大导致出错.但是,若采用先“剥离”的方法,则只要一次求导,运算难度减小,简单讨论下就能完美地得到答案.笔者查阅了2016年的各市期末试卷,发现有很多类似的问题,故把“f(x)lnx”问题的一类简化算法写出来,与读者一起分享.首先我们通过例1来对比两种算法的优劣.
例1 已知函数f(x)=(x+1)lnx-ax+a(其中a为正实数,且为常数).
1)若函数f(x)在区间(0,+∞)上单调递增,求实数a的取值范围;
2)若不等式(x-1)f(x)≥0恒成立,求实数a的取值范围.
(2017年江苏省苏锡常镇一模数学试题第19题)
解 1) 0 2)方法1 ①当x=1时,0≥0,从而a∈R. ②当x>1时,f(x)≥0恒成立.因为 设p(x)=xlnx+(1-a)x+1,则 p′(x)=lnx+2-a, 当0 p(x)>p(1)=2-a>0, 进而 f′(x)>0, 即f(x)在(1,+∞)上单调递增,故f(x)>f(1)=0,满足题意.当a>2时,令p′(x)=0,则 x=ea-2>1. 当x∈(1,ea-2)时,p′(x)<0,p(x)单调递减,从而 p(x) 则 因此当x∈(1,ea-2)时,f(x)单调递减,则当x∈(1,ea-2)时,f(x) ③当0 设p(x)=xlnx+(1-a)x+1,则 p′(x)=lnx+2-a. 当a>2时,因为0 p(e-a)=e-a(1-2a)+1, 设h(a)=e-a(1-2a)+1,则h′(a)=e-a(2a-3)>0,所以h(a)在(2,+∞)上单调递增,即 亦即p(e-a)>0.函数p(x)在(e-a,1)上连续,由零点存在性定理,p(x)在(e-a,1)上存在零点.又p(x)在(e-a,1)上单调递减,于是p(x)在(e-a,1)上存在唯一的零点,记为x0.因此,当x∈(x0,1)时,p(x)<0,f′(x)<0,即f(x)在(x0,1)上单调递减.因为f(1)=0,所以f(x0)>0,矛盾. 当0 综上所述,0 方法2 ①当x=1时,0≥0,从而a∈R. 综上所述,对于工程造价信息化建设工作的落实,其在当前确实表现出了较强的发展作用价值,相对于传统工程造价管理模式具备多方面优势,这也就需要加大推广力度,详细分析探究现阶段存在的各个方面问题,然后采取有效措施予以解决。 设h(x)=x2+(2-2a)x+1,其中x>1,当Δ≤0时,0 当Δ>0时,a>2.令h(x)=0,得 因为h(1)=4-2a<0,所以当x∈(1,x2)时,h(x)<0,g′(x)<0,从而g(x)在(1,x2)上单调递减.又g(1)=0,得g(x2)<0,不合题意. 设h(x)=x2+(2-2a)x+1,其中0 又h(1)=4-2a<0,当x∈(x1,1)时,h(x)<0,g′(x)<0,于是g(x)在(x1,1)上单调递减.又因为g(1)=0,所以g(x2)>0,不合题意. 综上:0 前苏联教育家维果斯基提出:教育对儿童的发展能起到主导作用和促进作用,但需要确定儿童发展的两种水平:一种是已经达到的发展水平,另一种是儿童可能达到的发展水平,表现为“儿童还不能独立地完成任务,但在成人的帮助下,在集体活动中,通过模仿,却能够完成这些任务”.这两种水平之间的距离,就是“最近发展区”.从“最近发展区”设计算法,能加速学生数学运算素养的提高. 例2 已知函数f(x)=xlnx,g(x)=λ(x2-1)(其中λ为常数). 2)若对任意x∈[1,+∞),不等式f(x)≤g(x)恒成立,求实数λ的取值范围. (2016年江苏省镇江市期末试题第20题改编) 所以h(x)在[1,+∞)上单调递减.又因为h(1)=0,所以h(x)≤h(1)=0. 2)由题意,当x≥1时,不等式xlnx-λ(x2-1)≤0恒成立.不等式两边同除x,得 ①当λ≤0时,由x≥1,得h′(x)≥0,因为h(x)在[1,+∞)上单调递增,又h(1)=0,得h(x)≥0,舍去. h′(x)≤0, 得h(x)在[1,+∞)上单调递减.又因为h(1)=0,所以h(x)≤0,满足题意. 因为m(1)=1-2λ>0,所以当x∈(1,x2)时,m(x)≥0,h′(x)≥0,从而h(x)在(1,x2)上单调递增.又因为h(1)=0,所以h(x2)>0,矛盾. (2016年江苏省常州市数学期末试题第19题) 解 由题意,当x≥1时,x2lnx-x+1-t(x-1)2≥0恒成立.两边同时除以x2,得 g′(x)≥0, 因为g(1)=0,所以g(x)≥0. 学生的数学运算能力急需改善,具体表现在对运算方向的探索和运算程序的设计上存在不足.为此,教师在平时的教学中对一些运算复杂的问题,要能带领学生全方位地选择算法,择优设计运算程序,从而将提高学生的数学运算核心素养落到实处.以上是笔者对“f(x)·lnx”这类问题的一类简化算法的研究,先拨开“f(x)”化简原式,然后借助简单的分类讨论,并且坚持算下去,最终圆满解决问题. 著名教育家波利亚曾说过:“没有一道题是可以解决得十全十美的,总剩下些工作要做,经过充分地探讨与钻研,总会有点滴的发现,总能改进这个解答,而且在任何情况下,我们都能提高自己对这个解答的理解水平.” [1] 陈玉娟.例谈高中数学核心素养的培养[J].数学通报,2016(8):34-36. 2017-06-20 王 强(1989-),男,江苏泰州人,中学二级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)09-13-03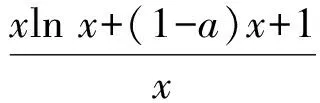
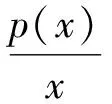
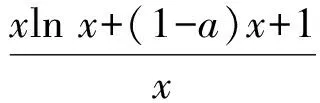
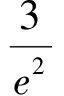


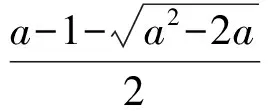
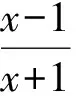

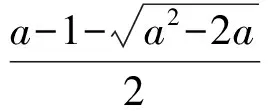
2 算法应用,提升素养