基于自适应K阶差分演化的多目标优化算法

谢大同

(福建商学院 信息管理工程系，福建 福州，350108)

基于自适应K阶差分演化的多目标优化算法

谢大同

(福建商学院 信息管理工程系，福建 福州，350108)

差分演化算法已经被成功地用于解决单目标和多目标优化问题，然而它的搜索能力受限于所使用的变异模式和控制参数。为此，提出一种新的变异模式——K阶差分，并引入参数自适应机制，设计了一个基于自适应K阶差分演化的多目标优化算法。与NSGA-II、DEMO的仿真实验比较结果表明，该算法在ZDT测试问题上能获得较好的优化效果。

差分演化；多目标优化；参数自适应；K阶差分

0 引言

差分演化算法(Differential Evolution，简称DE)是Storn和Price[1]提出的一种智能优化方法，具有简单、高效的特点，已经被成功地用于解决单目标和多目标优化问题。然而，差分演化算法对杂交概率和缩放因子这两个参数比较敏感。一些研究者对算法参数的设置进行了探讨，给出了一些指导性意见。譬如Gämperle[2]、Liu[3]等人建议缩放因子设为0.6，杂交概率在0.3到0.9之间选取。Rönkkönen[4]等人认为，F最好设置在0.4到0.95之间，其中0.9是一个比较好的初始选择，而对于CR，他们认为在0到0.2之间的值适合于可分离的函数，而在0.9到1.0之间的值适合于存在参数依赖的函数。类似的参数设置建议还有很多，但是它们一般都局限于部分问题，甚至有些建议相互矛盾。因此，由算法在演化过程中对参数进行自适应调节，已经成为差分演化算法的一个研究热点。在单目标优化领域，人们提出了差分演化算法的一些参数自适应版本。实际上，这些参数自适应策略也可以用于多目标优化问题。Abbass[5]提出一种参数自适应的多目标差分演化算法，在该算法中，杂交概率成为个体编码的一部分，通过演化算子自适应地进行调整，而缩放因子则通过高斯分布N(0，1)产生。Qian和Li[6]提出ADEA算法，该算法使用个体的拥挤距离对参数进行自适应调整，使用Pareto非支配排名和修改的拥挤距离对个体进行选择。此外，一些研究者对差分演化算法的变异模式进行了比较研究，发现各种变异模式在各类优化问题上的表现互有优劣，也设计了新的变异模式。Mezura-Montes[7]比较了8种不同的变异模式在13个测试问题上的性能。FAN和LAMPINEN[8]将所有可能的变异模式概括为四组，并提出一种对个体随机分组或者按适应度分组后采用两组的中心来产生差分向量的变异策略。

现有差分演化算法的变种基本上都按照基本差分演化算法中使用成对向量之差的方式来构造差分向量。本文从差分演化的这种操作特点联想到数学上的差分概念，提出一种新的差分变异模式——K阶差分变异；同时，在差分演化算法中自适应地调节缩放因子、杂交概率和变异模式；最终，设计出一个基于自适应K阶差分演化的多目标优化算法(SKDEMO，Self-adaptive K-order Differential Evolution Multi-objective Optimization)。

1 自适应K阶差分演化

1.1 一种新的变异模式

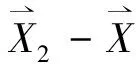
图1 K阶差分演化算法的主体部分Fig.1 The main body of K-order differential evolution

如果按数学上K阶差分(K≥2)的概念来构造差分向量，实际上是用三个或三个以上的解向量来产生一个差分向量，这种差分向量的构造方式将使得算法既可能获得多样性更好的解，也可能产生对目标向量进行局部搜索的效果。以2阶差分变异为

图2 阶差分变异过程的示意图Fig.2 Diagram of 2-order differential variation

2.2参数自适应

由于差分演化存在对参数敏感的问题，我们为差分演化算法的缩放因子F、杂交概率CR、变异模式K设计了自适应调节策略。

差分演化的参数自适应调节机制采用统计建模的方法实现。首先，将F、CR、K作为个体编码的一部分。从而，种群中的第i个个体可表示为(Xi,Fi,CRi,Ki)。然后，采用(0.1, 1)和(0.01, 1)之间产生的均匀分布随机数分别对F和CR这两个参数进行初始化，K则随机设置1或2(当K值为1时表示执行1阶差分变异，为2时执行2阶差分变异)。在差分演化算法执行过程中，记录下被改善个体所使用的F、CR和K，并分别记录下每种变异模式下被改善个体的数量。每20代期间，若没有个体被改善，则分别采用(0.1，1)和(0.01，1)之间产生的均匀分布随机数重新初始化个体的F和CR，否则若被改善个体的参数值之间的最大差距超过0.1，则从被改善个体中随机选取参数赋予未改善的个体，未超过0.1则根据被改善个体的参数值分别计算F和CR的均值Fmean和Cmean，并以正态分布N(Fmean，0.052)和N(Cmean，0.022)为未改善的个体产生新的F和CR值。未改善个体的变异模式按两种变异模式下改善个体的概率采用轮盘赌策略进行设置。参数自适应的K阶差分演化多目标优化算法SKDEMO的步骤如下：

1 G=0，初始化种群PG={(X1，F1，CR1，K1)，(X2，F2，CR2，K2)，…，(XNP，FNP，CRNP，KNP)}2 将PG中的非支配解放入档案集AG3 While停机条件不满足do4 Fori=1toNPDo5 Selectrandomlyr0≠r1≠…≠rk+1≠i6 jrand=randint(1，D)7 Forj=1toDDo8 If(randj(0，1)=0 1then31 从被改善个体中随机选取参数赋予未改善的个体32 采用轮盘赌策略为未改善个体设置K值33 Else34 计算被改善个体中缩放因子和杂交概率的均值Fmean、CRmean35 用N(Fmean，0 052)和N(CRmean，0 022)为未改善的个体生成参数

36 采用轮盘赌策略为未改善个体设置K值37 Endif38 EndIf39 G=G+140 EndWhile41 输出结果

2 数值实验

2.1实验设置

为了验证算法的性能，在ZDT1、ZDT2、ZDT3、ZDT4和ZDT6这5个测试问题上对NSGAII、DEMO、未使用参数自适应机制的K阶差分演化算法(记为KDEMO)和使用参数自适应机制的K阶差分演化算法(记为SKDEMO)进行比较实验。四个算法共同的参数设置为：档案集规模为200，运行次数为50，停机条件为评价次数达到100000；NSGA-II和DEMO的种群规模设为200；其它两个算法的种群规模设为50。此外，按照文献[9]，将NSGA-II的杂交概率设为0.9，变异概率为1/n (n是决策变量的数目)，杂交和变异算子的分布指数均为20。对于DEMO，使用文献[10]给出的三种算法中总体表现最好的DEMO/parent算法，且杂交概率和缩放因子也分别设为0.3和0.5。KDEMO采用2阶差分变异模式，其杂交概率和缩放因子取值与DEMO一致。

3.2 实验结果及分析

表1、表2和表3分别列出了NSGA-II、DEMO、KDEMO和SKDEMO在5个测试问题上得到的IGD、Spacing、超体积这三个指标的均值和标准差(记为“均值(标准差)”的形式)。

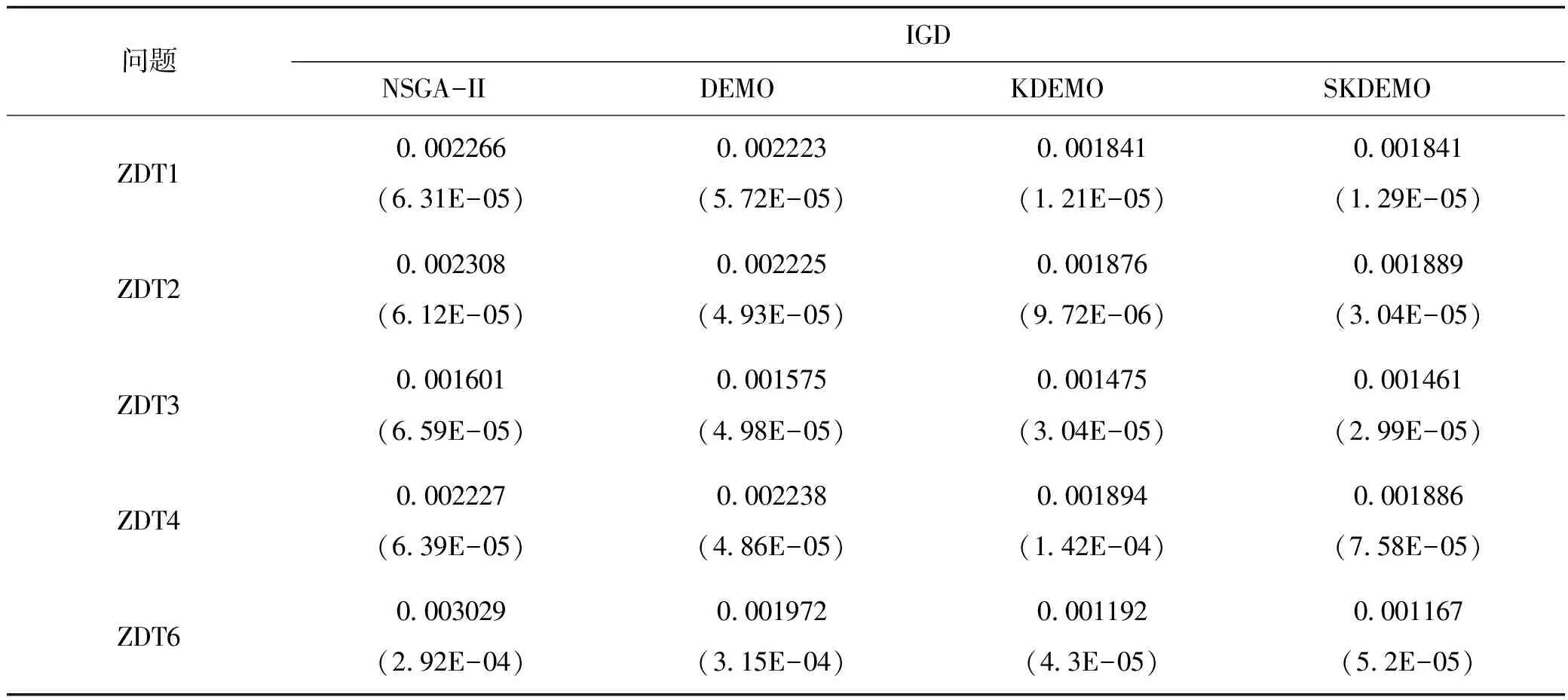
表1 四个算法在ZDT测试问题集上的收敛性能指标IGD的均值和标准差

表2 四个算法在ZDT测试问题集上的分布性能指标Spacing的均值和标准差

表3 四个算法在ZDT测试问题集上的性能指标超体积的均值和标准差

三个表中的数据表明，KDEMO和SKDEMO在5个ZDT测试问题上与NSGA-II和DEMO相比具有明显的性能优势(粗体文字标明了四种算法中最好的平均性能指标值)，而KDEMO算法与SKDEMO算法的性能几乎不分伯仲。单纯从收敛性能来看，SKDEMO的效果更好，而从分布性能来看KDEMO更优。另外，尽管KDEMO在ZDT2上表现出IGD和Spacing指标值都优于SKDEMO，但按照超体积指标，SKDEMO优于KDEMO。在ZDT3上，SKDEMO的IGD和Spacing指标均优于KDEMO，但在超体积指标上却劣于KDEMO。这一现象与一些文献中提到的IGD和Spacing指标不能准确反映算法性能优劣的结论吻合。

为了更准确地区分KDEMO和SKDEMO在不同问题上的性能，将两个算法在各问题上运行50次的超体积性能指标值使用Kruskal-wallis检验方法进行统计比较，统计检验结果如表4所示。表中数值表示由行对应的算法A和列对应的算法B配对在单尾检验下得到的p值，零假设为“A的结果不优于B的结果”，备择假设为“A的结果优于B的结果”，显著性水平α设为0.05。根据表4的数据可知，SKDEMO在5个ZDT测试问题上的超体积指标均优于KDEMO。

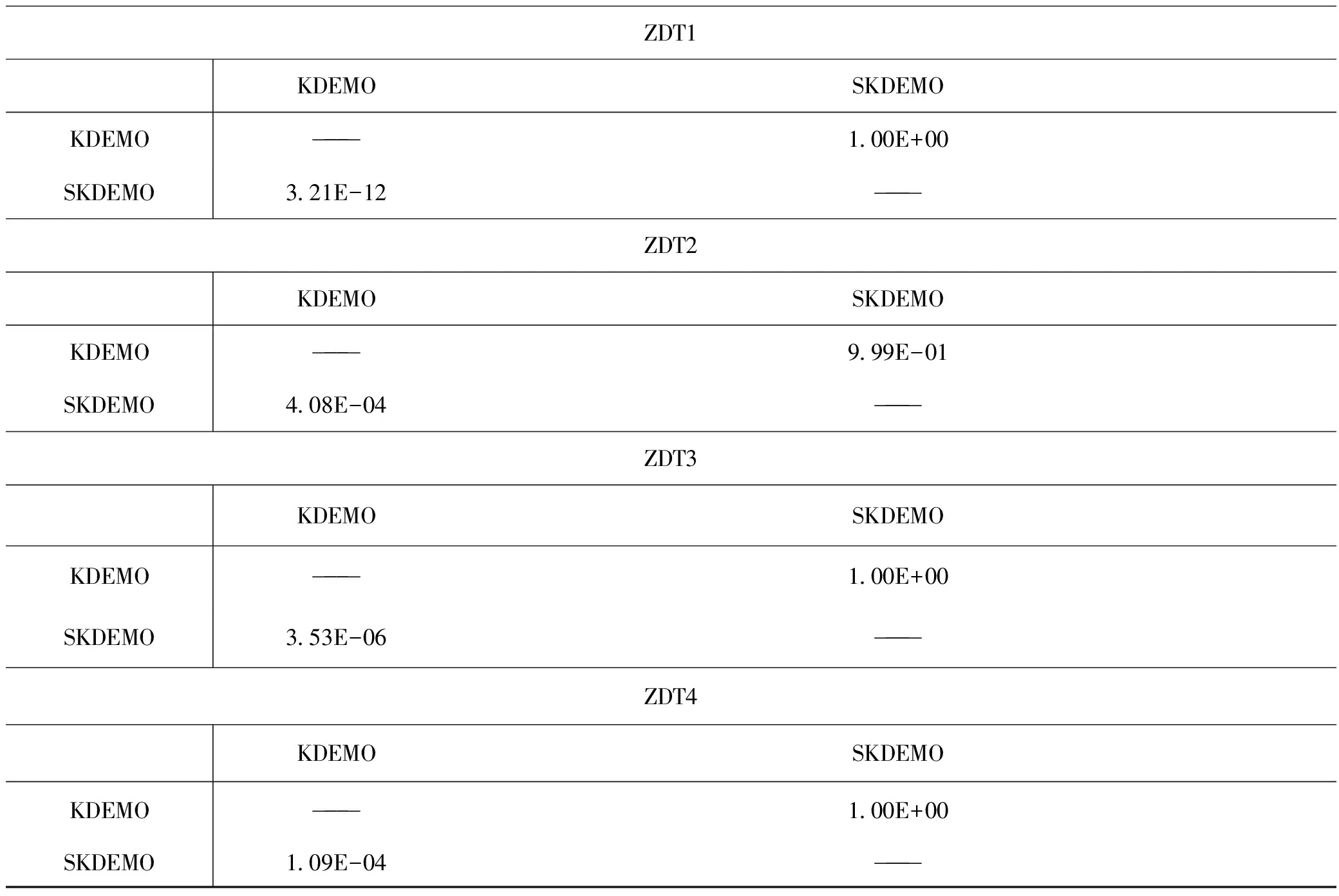
表4 在5个ZDT测试问题上分别执行KDEMO和SKDEMO各50次所得超体积指标值的Kruskal-Wallis检验结果

——续表4

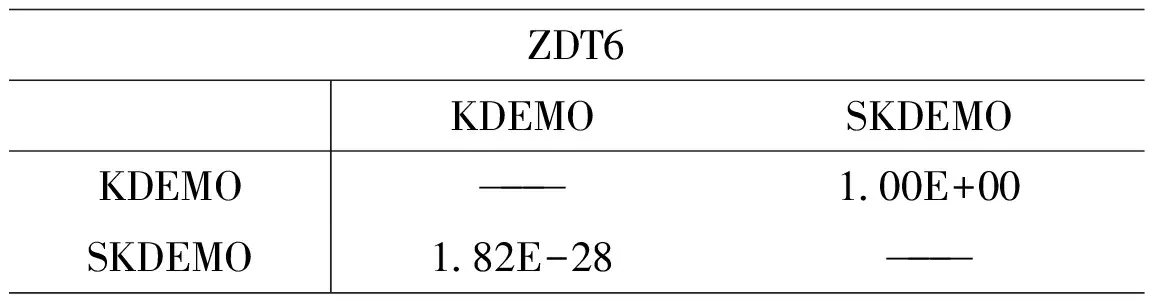
ZDT6KDEMOSKDEMOKDEMO———1 00E+00SKDEMO1 82E-28———

上述实验结果表明，SKDEMO所采用的自适应机制是有效的。为了帮助进一步理解SKDEMO的参数自适应机制，用图3～图7来描述演化过程中优秀参数的均值和个体被改善数量的均值的变化趋势。

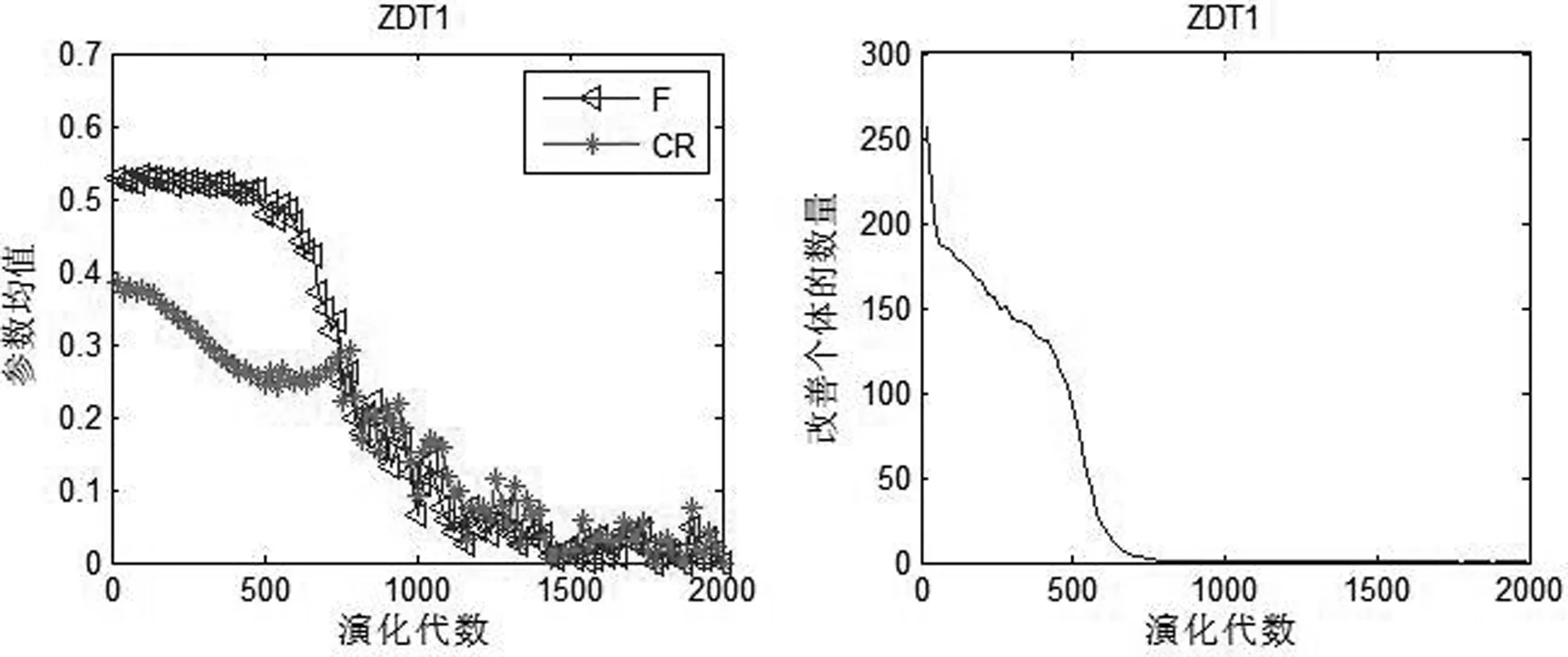
图3 SKDEMO 在ZDT1上执行时优秀参数均值和个体被改善数量均值的变化趋势Fig.3 Variation tendencies of the mean values about perfect parameter values and the count of improved individuals with SKDEMO executed on ZDT1

图4 SKDEMO 在ZDT2上执行时优秀参数均值和个体被改善数量均值的变化趋势Fig.4 Variation tendency of the mean values about perfect parameter values and the count of improved individuals with SKDEMO executed on ZDT2

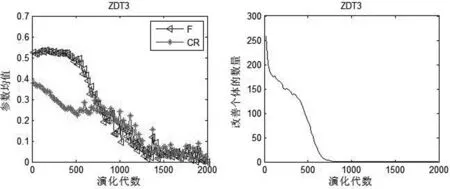
图5 SKDEMO 在ZDT3上执行时优秀参数均值和个体被改善数量均值的变化趋势Fig.5 Variation tendency of the mean values about perfect parameter values and the count of improved individuals with SKDEMO executed on ZDT3

图6 SKDEMO 在ZDT4上执行时优秀参数均值和个体被改善数量均值的变化趋势Fig.6 Variation tendency of the mean values about perfect parameter values and the count of improved individuals with SKDEMO executed on ZDT4

图7 SKDEMO 在ZDT6上执行时优秀参数均值和个体被改善数量均值的变化趋势Fig.7 Variation tendency of the mean values about perfect parameter values and the count of improved individuals with SKDEMO executed on ZDT6

图3～图7表明，在演化前期，被改善的个体较多时，F的取值在0.5附近，CR的取值在0.3附近，接近文献[10]中所建议的参数。而后期被改善的个体变少，主要原因在于演化后期算法开始收敛，种群中趋同的个体也越来越多。此时算法主要对优秀个体进行精细搜索，因此缩放因子值会变小，而杂交概率也变小，即个体执行差分变异的概率降低。从图3～图6可看出，前500代缩放因子基本上在0.5附近，而杂交概率波动比较明显，个体改善的数量变化趋势陡峭，说明此段时间算法性能受杂交概率的影响较大。从图6可知，在500代时，个体改善的数量最大，此时杂交概率较小，而在1000代时杂交概率值较大，个体改善的数量几乎为0，因此可以认为，对于ZDT4而言，杂交概率在0.1附近时更容易改善个体。图7表明，ZDT6使用0.4附近的值作为杂交概率时，更容易改善个体。

3 结束语

利用基本差分演化算法中构造差分向量的特点，结合数学上的差分概念，设计了一种K阶差分变异模式，对差分演化的变异方式进行了延伸。实验结果表明，基于2阶差分变异模式的多目标演化算法KDEMO在ZDT测试问题上的寻优能力比NSGA-II和DEMO更强，而在KDEMO算法基础上加入参数自适应调节机制构造的算法SKDEMO的性能比KDEMO更好。在种群规模允许的范围内，可将差分向量的构造方式拓展为使用3阶、4阶甚至更高阶的差分变异模式。下一步的工作将探究差分演化算法采用不同阶的差分变异模式在各种问题上的优化效果。同时，也有必要从理论上分析K阶差分变异模式的收敛性。

[1]STORN R，PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization，1997 (11): 341-359.

[2]GAMPERLE R，MULLER S D，KOUMOUTSAKOS P. A parameter study for differential evolution[J]. Advances in intelligent systems，fuzzy systems，evolutionary computation，2002 (10): 293-298.

[3]L J. On setting the control parameter of the differential evolution algorithm[C]. Brno：The 8th international Mendel conference on soft computing，2002.

[4]RONKKONEN J，KUKKONEN S，PRICE K V. Real-parameter optimization with differential evolution[C]. Edinburgh：IEEE Congress on Evolutionary Computation 2005， 2005.

[5]ABBASSH A. The self-adaptive pareto differential evolution algorithm[C]. New Jersey：IEEE Congress on Evolutionary Computation 2002，2002.

[6]QIAN W. Adaptive differential evolution algorithm for multiobjective optimization problems[J]. Applied Mathematics and Computation，2008 (201): 431-440.

[7]MEZURA M E，VELAZQUEZ J，COELLO C A. A comparative study of differential evolution variants for global optimization[C]. Seattle：The 8th annual conference on Genetic and evolutionary computation，2006.

[8]FAN H，LAMPINEN J. A trigonometric mutation operation to differential evolution[J]. Journal of Global Optimization，2003 (27): 105-129.

[9]KALYANMOY D，AMRIT P，SAMEER A，et al. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation，2002 (6): 182-197.

[10]TEA R，BOGDAN F. DEMO: differential evolution for multiobjective optimization [C]. Guanajuato: The third international conference on evolutionary multi-criterion optimization，2005.

(责任编辑：杨成平)

Multi-objective Optimization Algorithm Based on Self Adaptive K-order Differential Evolution

XIE Da-tong

(Department of Information Management and Engineering,Fujian Commercial College, Fuzhou 350108, China)

Differential evolution has been successfully employed to solve single-objective and multi-objective problems. However, its search ability is significantly influenced by its variation patterns and control parameters. Therefore, a new variation pattern named K-order difference is proposed in this paper. Then, a multi-objective optimization algorithm, SKDEMO, which is based on K-order differential evolution and self adaptive parameter adjustment mechanism, is designed to solve multi-objective problems. The experiments on five ZDT benchmark problems show that SKDEMO exhibits better performance than NSGA-II and DEMO.

differential evolution; multi-objective optimization; parameter self-adaptation; K-order difference

2017-04-20

福建省中青年教师教育科研项目(科技类)“多目标优化问题的K阶差分演化算法研究”(JA13400)。

谢大同(1977-)，湖南双峰人，副教授，博士。研究方向：智能计算、软件工程。

TP311

A

2096-3300(2017)03-0091-10