利用GeoGebra软件辅助初中函数教学案例的研究

聂霞

[摘 要] 本文利用GeoGebra软件引导学生进行一次函数的探究实验，让学生通过观察、猜想、实验、归纳、推理、交流等数学活动过程，体会和学会探索问题的一般方法.

[关键词] GeoGebra软件；使用；函数；教学案例

引言

初中数学新课标的出现，大力加强了信息技术在数学教学中的应用，强调以学生动手为主的数学学习方式，目的是提高学生学习数学的积极性，提高学生的数学应用意识，培养学生利用所学的数学知识和计算机技术去认识问题和解决实际问题的能力. 一方面，这一整合有利于学生对数学本质的理解以及数学应用能力的提高；另一方面，也增加了学习时间和学习难度. 所以，要用好新课标，必须采取有别于传统的数学学习方式. 在新课标的教学中，利用信息技术为数学思想方法注入更多、更广泛的内容，能使学生摆脱繁重的、乏味的数学演算和数值计算，能促进数学同其他学科之间的结合，从而使学生有时间去做更多的创造性工作，并引导学生对某一数学知识进行探究，从而引入、猜想、归纳、验证，使学生亲历数学建构过程，逐步掌握认识事物、发现真理的方式和方法，培养创造能力，提高数学素养. 在新课标教学实践中，笔者利用GeoGebra软件采用验证型实验和设计型实验进行教学.

GeoGebra软件使用简介

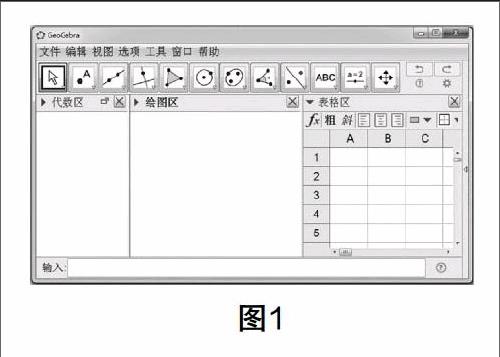
GeoGebra软件是由美国佛罗里达州亚特兰大大学数学系教授Markus Hohenwarter设计的，它是集代数、几何与微积分于一体的动态数学教育软件. GeoGebra 能够做到几何图形与代数方程的同步变化，展示数学对象动态生成的全过程，是一款专门为中学数学教育设计的动态数学软件，且入门容易，操作简单方便，有着强大的图形和图像功能. 打开GeoGebra软件窗口，如图1， 菜单上方为工具栏，有各种绘图工具和辅助工具，左侧有一个“代数区”，用来显示所输入的代数表达式，中间有一个“绘图区”，可使用绘图工具在绘图区中利用鼠标作图，也可在命令栏中输入命令，在绘图区绘图. 右侧可显示“电子表格区”，通过“查看”菜单可显示出. 每个单元格都对应相应的名称，不但可以输入数值，还可以输入数学对象，在电子表格中输入的数学对象会在绘图区中给出相对应的图像，并以单元格的位置名称命名. 下侧是命令列，可直接输入代数式及相关函数. GeoGebra软件能够同时处理代数与几何功能，若利用工具栏在绘图区画出图形，则代数区就会出现对应的方程表达式. 反过来，若利用命令列输入代数方程式，则绘图区便出现对应图形，代数区也显示出相应的表达式. 若代数式参数发生改变，则绘图区的图形也会随之改变，反之亦可. 它把几何图形和代数式的关系动态地结合在一起. 对于GeoGebra软件的详细使用说明，可以点击菜单中的 “帮助”，通过联网查看相关的教程或者进入GeoGebra论坛进行学习.

一次函数的图像和性质的实验探究

（一）验证型实验的构建

1. 研究问题

非洲大草原上一只矫健的野兔遇到了一只饥饿的豺，野兔的奔跑速度恒为每秒4.5米，豺的奔跑速度恒为每秒5米. 遇到时，二者仅相距5米，假定二者同时起跑.

（1）分别写出二者距豺起跑点的距离y与出发的时间x的关系式；

（2）结合实际情况，饥饿的豺最多只能坚持跑10秒，则谁能获胜？

2. 分析问题

显然，根据正比例函数和一次函数的定义及一般形式，我们可以很轻松地写出二者距豺起跑点的距离y与出发的时间x的关系式：

y=5x（豺）和y=4.5x+5（野兔）

那么，结合实际情况，饥饿的豺最多只能坚持跑10秒，谁能获胜呢？要想解决这个问题，我们不妨借助函数图像来进行研究.

3. 实验操作步骤与指导

Step1 在GeoGebra软件的命令窗口中键入命令：

>> y=5x

>> y=4.5x+5

于是在代数区中便会显示出——

直线 f ： y=5x

g ： y=4.5x+5

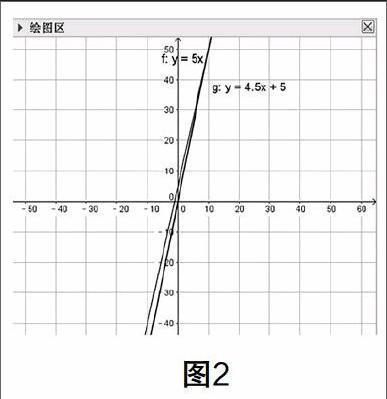
在绘图区中便会显示出二者的函数图像，如图2.

从图中可以看出，二者均单调递增，且从图中可以明显地看出二者的函数图像随着x的增大而不断靠拢，最终在x=10（秒）处相交，即豺和野兔之间的距离随着时间的推移不断缩小，并在10秒钟时豺将野兔捕获！

4. 实验结论的验证

由于豺要将野兔捕获，则二者距豺原始起跑点的距离y（米）必相等，于是有5x=4.5x+5，即0.5x=5，所以x=10（秒），即豺在第10秒時将野兔捕获.

通过以上实验操作，学生能观察出二者的图像特征，找到二者的变化规律并最终对问题进行验证.

（二）设计型实验的构建 1

1. 研究问题

正比例函数y=kx（k≠0）的图像特征和函数性质.

2. 实验要求与建议

要求：请同学们自主探索后彼此之间分小组讨论研究，填写实验报告表中的相关内容.

建议：在同一图形窗口界面中将定义域区间取为[-10，10]，参数k分为k>0 和k<0进行研究. （实验时k的值由学生自己决定）

3. 实验报告表的设计样例（如表1）

（三）设计型实验的构建2

1. 研究问题

k，b对一次函数y=kx+b（k≠0，x∈R）的图像和性质有何影响？

2. 实验要求与建议

要求：从无序实验到有序探索，请同学们彼此之间分小组讨论研究，并填写实验报告表中的相关内容.

建议：将定义域区间取为[-10，10]，k，b两个参数要一个一个研究，研究一个参数时，另一个参数保持不变.

3. 实验报告表的样例参数图像实验结论（如表2）

（四）设计型实验的构建3

1. 研究问题

k，b对一次函数y=kx+b（x∈R）的图像位置有何影响？

2. 实验要求与建议

要求：请同学们独立研究，填写实验报告中的相关内容.

建议：将定义域区间取为[-10，10]，根据k，b的符号变化，探究画图.

3. 实验报告表的样例（如表3）

课外实验探究设计样例

1. 研究问题

探究函数y=kx+b与y=kx+b的图像特征和函数性质

命令提示：在GeoGebra中用abs（x）表示函数x.

2. 实验报告表的设计样例（如表4）

结束语

在初中数学新课标教材的基本初等函数的教学过程中，利用GeoGebra软件让学生在计算机上进行自主探究实验，让学生通过观察、猜想、实验、归纳、推理、交流等数学活动过程，体会和学会探索问题的一般方法，不仅可以使学生掌握并应用函数性质解决问题，还可以培养团队意识和大胆猜想、乐于探究的良好品质，让学生体验到成功的喜悦.