引导学生发现数学之美

陈春花

摘 要：高中数学是一门极具魅力的学科，每一个角落都散发着美好。如果能将这些美好的点滴都传达到学生心中，必然能够为教学提速与优化提供强大驱动。笔者从基本教学理论出发，从多角度探寻高中数学之美的所在，结合实践经验提出了一些教学建议，望对广大教师有所助益。

关键词：高中；数学；美好

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2017）08B-0101-02

高中数学学习中不是只有公式与计算，更有着诸多美的享受。如果学生们能够从感受美好的角度出发，来认知学习过程，必将为整个高中数学教学带来全新的面貌与体验。这也是对高中数学教学提出的一个创新性的设想。纵观当前的教学过程，总是让学生们感到自己是在被高考的重压逼迫着学习，求知过程陷入被动，实效并不理想。转换教学视角，从享受学习美好的角度出发，也许能够为高中数学教学带来更为强大的生命力。

一、着眼细节，发现高中数学的严谨之美

数学是一门十分讲求细节与严谨的学科。很多时候，学生们之所以会在解答数学问题的时候出现错误，都是因为在不经意间忽略了某个小细节，导致整个数学知识大厦的坍塌。为了让学生们的学习态度更加积极，我们不应将这种对细节的追求视为一种负担，而应将其视为一种严谨之美的表现来对待。

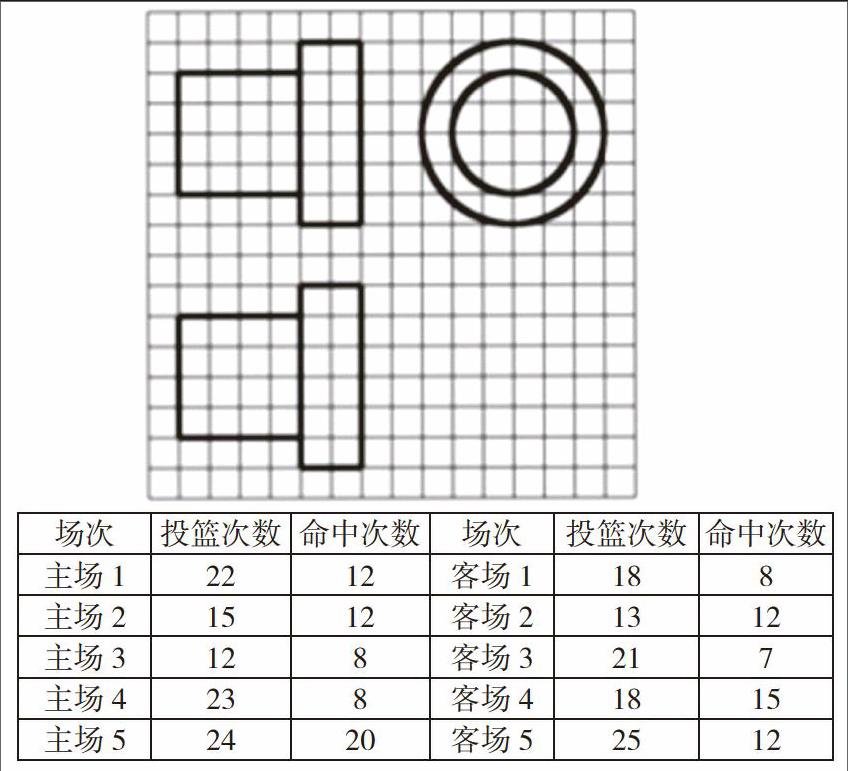
例如，为了让学生们在立体几何的学习过程中充分关注到空间处理的细节所在，我请大家思考如下问题：如下图所示，网格纸当中的每一个小正方形的边长均为1厘米，其中用粗线所表示出的是某种机械零件的三视图。已知，这种零件是由一个底面半径是3厘米，高是6厘米的圆柱体材料削切得到的，那么，削切掉的材料体积与材料原本的总体积数量之比是多少？想要正确解答这个问题，学生们需要根据三视图准确把握零件的形状，并将已知条件中的数值匹配进去进行分析。每个过程都从细节考察了大家对立体几何知识的掌握。

二、着眼方法，发现高中数学的规律之美

高中阶段出现的数学知识内容可谓数量庞大。如果只是一味地逐个进行分析和记忆，还要保证每一个知识点的学习质量，相信没有谁能够妥善应对如此之大的工作量。因此，我们需要寻找规律与方法，将具体零散的知识内容串连起来，为高中数学学习开辟出一条捷径。

例如，在对解析几何的内容进行教学时，我适时引入了这样一道习题：已知，点P是抛物线y=x2上的一个动点，该点P在x轴上的射影是M，并有点A的坐标是（2，0），那么，|PA|+|PM|能够取得的最小值是多少？如果单从问题表面来看这道题目，显然无法知晓最小值的取得条件。既然抛物线是确定的，其中的一些点线关系也是确定的，为何不把图形画出来看看呢？果然，随着图形的画出，题目当中的数量与位置关系瞬间明朗了。通过模拟点P的运动过程，|PA|+|PM|取得最小值的情形直观可得。由此，数形结合的规律方法体现得颇为明确。

高中数学当中常用的思想方法有很多，它们都是从诸多具体问题的解答过程里提炼总结出来的。为学生们创造机会，让他们能够亲身经历这些方法的得出，便能够真实地触摸到知识规律的存在。这种意识建立起来之后，学生们就会深深地感受到潜藏在数学知识背后的规律之美，如同一条线穿梭于知识内容之间，让整个学习过程顺畅高效。

三、着眼实践，发现高中数学的应用之美

数学来源于生活，而又回归于生活。我们之所以要研究数学，归根结底还是为了解决实际生活当中出现的问题。否则，数学便会成为一门空中楼阁式的枯燥理论，毫无生机与价值。在高中阶段的各类数学习题当中，我们也经常可以看到实践性问题的影子，这也从另一个角度强调了学以致用的重要性。它不仅是数学学习的必然要求，更是高中数学应用之美的集中体现。

例如，在对概率统计的内容进行教学时，我在课堂上引入了这样一道题目：下面表格当中所显示的是小王在10场篮球比赛当中的投篮情况。其中，每一场比赛之间相互没有影响。那么，（1）从上述10场比赛当中任意选出一场，小王的投篮命中率高于0.6的概率是多少？（2）从上述10场比赛当中任意选择一场主场比赛和一场客场比赛，小王的投篮命中率一场高于0.6，另一场不高于0.6的概率是多少？（3）如果以x来表示上述10场比赛中小王投篮命中率的平均数，并以X来表示任意一场比赛中的投篮命中次数，则E（X）和x的大小关系如何？在实际生活的背景下运用概率统计的方法进行分析，学生们的关注热情瞬间增加了许多，学习效果也比单纯的理论讲解要理想不少。

四、着眼开放，发现高中数学的灵活之美

高中数学的生命力不仅表现在它向实际生活的迁移过程中，还与知识内容的灵活开放息息相关。毫不夸张地说，高中数学当中每一个模块的知识内容都不是固定死板地存在着。只要细细寻找，总能够从中发现可以进一步灵活发展的切入点。这就是数学知识不断开放的基点。富于变化，灵活开放，也是高中数学的一个美好的来源。

例如，在对数列的知识进行教学时，我在一次课堂教学的结尾处请学生们试着思考这样一个问题：已知，数列{an}是一个等比数列，它的公比是q，前n项和是Sn。那么，能否找到一个常数c，使得数列{Sn+c}也是一个等比数列？如果能够找到，请写出这个常数c的值；如果不能找到，请说明常数c不存在的理由。这是一个典型的存在性开放问题，对学生们的思维能力提出了比较高的要求。与学生们所学习的具体知识内容相比，这个问题当中的数列显然抽象了许多。但是，我鼓励大家，虽然形式变得抽象了，但数列的特点和规律仍然存在。于是，学生们先假设存在合适的常数c，然后结合等比数列的性质将数列表示出来，并根据q=1和q≠1两种情况分别讨论研究，最终顺利确定了正确的常数c。思维过程并没有想象中的那么难。从这个开放的过程中，学生们看到了基本特点、性质在抽象问题中的普遍适用，并开始逐渐接受这种看似复杂的开放性问题了。

以往，一谈到开放性问题，学生们便会感到思维难度大，进而心存畏惧与抵触。这种消极的心理状态是很不利于高效教学的开展的。随着教师的不断引导，学生们逐渐开始扭转目光，将数学知识的灵活开放视为一种美好的源头，并享受这个持续深入探究的过程。这种转变是极具价值的，也是高中数学教学十分需要的。

其实，高中数学这门学科当中是不乏美好的。只不过由于升学考试的压力，迫使我们在学习数学知识时不得不掺杂进来很多功利性的心态，渐渐使得数学学习成为了一种极具压力的任务，让原本美好的知识体验失去了它应有的色彩。通过前文当中的叙述我们不难发现，从享受数学学习之美出发去感受知识，并不会干扰正常的教学效率，反而会让每个阶段的学习目标更加明确。作为一门灵动鲜活的学科，高中数学还有更多美好之处等着我们去探寻和发现，希望广大师生们能够在这种积极的氛围当中取得更大的教学进步。

参考文献：

[1]黃胜亮.数学教学中寓美于教之我见[J].数学学习与研究，2013，（7）.

[2]彭灵莉.让学生感受数学之美[J].科学咨询，2011，（1）.

[3]赵桂萍.引领学生发现数学之美[J].科学教育，2011，（4）.

[4]栾维莲.新课程背景下高中数学教学方法研究[J].中国校外教育，2017，（2）.endprint