分数阶互感及变压器模型的特性分析

刘 潇，张 波，谢 帆，丘东元

（华南理工大学电力学院，广州 510640）

分数阶互感及变压器模型的特性分析

刘 潇，张 波，谢 帆，丘东元

（华南理工大学电力学院，广州 510640）

目前涉及磁能耦合、电能转换等方面的分数阶特性研究较少，因此针对分数阶互感及变压器模型的特性进行了分析。首先分析了传统分数阶LC电路的阻抗特性和相位特性；沿用该分析方法，研究了分数阶互感及变压器模型的阻抗矩阵特性，分析了阻抗矩阵在不同阶数下的相位特性以及分数阶条件下特有的纯实部特性和纯虚部特性；最后推出不同阻抗特性下，阻抗频率、幅值与电感阶数的关系。从分析中可知，自感和互感的分数阶数增加了整个模型设计的自由度，更具有一般性。

分数阶；互感；变压器模型；阻抗特性

分数阶微积分（fractional calculus）是在经典微积分理论基础上产生的用以描述任意阶数微分和积分的数学分支，并已逐步成为多个科学工程领域的有力工具。文献[1]将分数阶微积分应用到经典电磁场中，提出了分数阶多极子的定义，并计算了其空间电势分布情况；文献[2]提出了一种分数阶正弦振荡器，并给出了设计步骤和实验模型；文献[3]提出了一种分数阶永磁同步电机，其控制策略更加简单灵活；文献[4]将分数阶微积分运算应用到遗传算法中，建立了分数阶传递函数模型；文献[5]应用分数阶微积分相关知识研究了反向热传导问题。文献[6-7]分析和总结了分数阶RLC并联电路的基本特征和规律；文献[8]讨论了分数阶RLC串联电路在电感、电容阶数相同时的复杂特性；文献[9]则研究了分数阶LC串联电路在电感、电容阶数不同时的幅值响应和相位响应。近几年来，无线电能传输得到了长足的发展[10，11]，其系统中蕴含的电感与电容特性也是一个研究的热点。然而，目前涉及到磁能耦合和电能转换等方面的分数阶特性系统分析还比较少。

本文首先分析了传统分数阶LC电路 （以串联为例）的阻抗特性，得出不同阻抗特性下幅值、频率与电感、电容阶数的关系，并分析了电感、电容阶数对相位特性的影响。随后，沿用这种分析方法，研究了分数阶互感及变压器模型的阻抗特性，分析了阻抗矩阵的相位特性以及分数阶条件下特有的纯实部特性和纯虚部特性，最后得出了不同阻抗特性下，阻抗频率、幅值与电感阶数的关系。由于分数阶互感电路及变压器模型的电路参数增加了自感和互感的阶数，因此该模型的设计自由度更高，应用范围更广。

1 分数阶阻抗

零初始条件下，对分数阶Caputo微分定义取拉氏变换，可以定义一种阻抗正比于sα的一般性分数阶电抗元件[12]，即

式中：β为分数阶电容元件的阶数；Lβ为分数阶电感；Cα为分数阶电容。令s=jω，则分数阶电感的阻抗和分数阶电容的导纳可变为

由式（2）可知，理想分数阶元件的阻抗（导纳）既有电阻（电导）分量，又有电抗（电纳）分量[13]。通过分数阶电感、分数阶电容的串并联，可以得到分数阶LβCα电路的基本拓扑，如图1所示。根据电路原理，串联电路的阻抗和并联电路的导纳互为对偶关系，若不改变对偶元件的值，则二者解的形式一致，只需计算其中一个便可得到另一个的解。因此，本文以分数阶电感Lβ和分数阶电容Cα组成的串联电路即分数阶LβCα电路为例来分析其阻抗特性。

图1 分数阶LβCα电路的基本拓扑Fig.1 Basic topologies of fractional-order LβCαcircuits

2 分数阶LβCα电路的特性分析

如图 1（a）为分数阶 LβCα串联电路的拓扑，根据式（3）可知，分数阶LβCα串联电路的阻抗可写为

式中：Re[Z（jω）]为阻抗实部；Im[Z（jω）]为阻抗虚部；｜Z（jω）｜为阻抗幅值；φ（ω）为阻抗相位角，则有

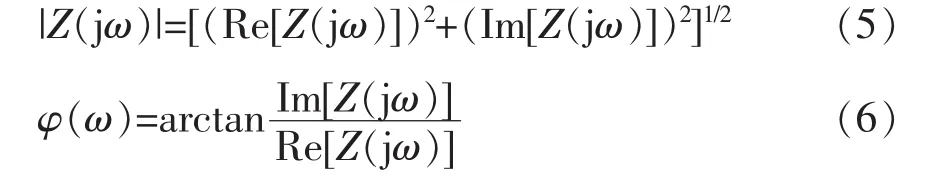
由式（4）可知，分数阶 LβCα串联阻抗特性不仅与电感L、电容C、频率ω有关，还与电感、电容的阶数β、α有关。在L、C、ω一定的情况下，随着α、β的改变，分数阶LβCα串联电路将会表现出不同的阻抗特性和相位特性。

2.1 阻抗特性

2.1.1 纯实部阻抗特性

令 Im[Z（jω）]=0，即

则电路呈现纯实部特性，即纯阻性，此时电路的角频率为

将ωr代入式（4），得到此时电路的阻抗为

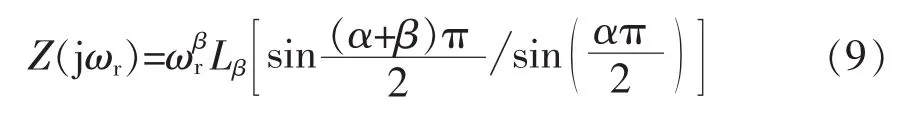
考虑一个相位周期，则有

不考虑Lβ、Cα同时表现感性或容性的情况 （实际上相当于一个分数阶电感或分数阶电容），可以得到 α、β 的范围分别为：0＜α＜2、0＜β＜2。

根据式（8），可以得到 ωr与 α、β 的关系曲线，如图2所示。由图2可知，随着α、β的增加，ωr有减小的趋势，且当α趋近于0+时，ωr出现最大值尖峰；当 α 趋近于 2-时，ωr趋近于 0。

图2 ωr与α、β的三维关系Fig.2 3-D view of ωrunder different α and β

由式（9）可知，当 α+β＜2 时，阻抗 Z（jωr）＞0，表现出正实部（正电阻）特性；当 α+β＞2时，阻抗 Z（jωr）＜0，表现出负正实部（负电阻）特性；当 α+β=2时，Z（jωr）=0。阻抗幅值|Z（jωr）|与 α、β 的关系如图 3所示。

图3 |Z（jωr）|与 α、β 的三维关系Fig.3 3-D view of|Z（jωr）|under different α and β

2.1.2 纯虚部阻抗特性

令 Re[Z（jω）]=0，即

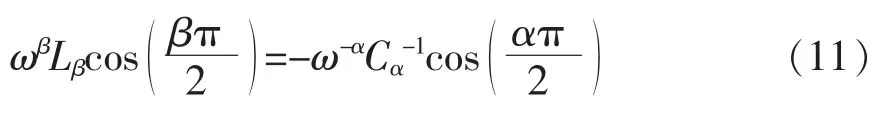
则电路呈现纯虚部特性，即纯感性或纯容性。由空间矢量关系可知，只有当 α＜1＜β 或 β＜1＜α 时，才能同时满足 0＜α＜2、0＜β＜2。 此时电路角频率为

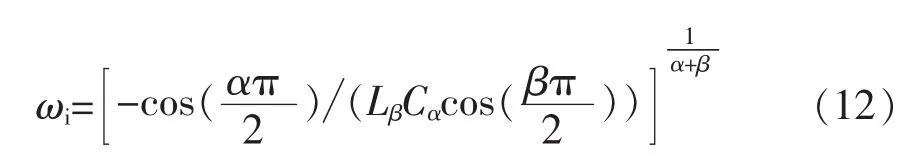
将ωi代入式（4），得到此时电路的阻抗为

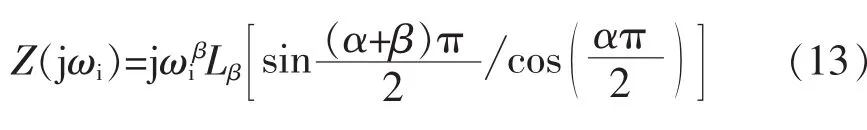
根据式（12）可以得到ωi与 α、β的关系曲线，如图 4所示。由图可见，在 α＜1＜β和 β＜1＜α两种情况下，ωi均随着β的增大而减小；当β＜1且α趋近于 1+时，ωi出现最大值；当 β＞1 时，ωi随着 α 的增大而减小。

根据式（13）可以得到阻抗幅值|Z（jωi）|与 α、β的关系曲线，如图5所示。由图可见，当α+β=2时，|Z（jωi）|=0 为最小值，α、β 越接近 1，|Z（jωi）|值越大；当 α＜ 1＜ β 时， β 对阻抗幅值|Z（jωi）|的影响要比 α大，也就是电感的阶数对阻抗幅值的作用更强；当β＜ 1＜ α 时，α 对阻抗幅值|Z（jωi）|的影响要比 β 大，也就是电容的阶数对阻抗幅值的作用更强。

图4 ωi与α、β的三维关系Fig.4 3-D view of ωiunder different α and β

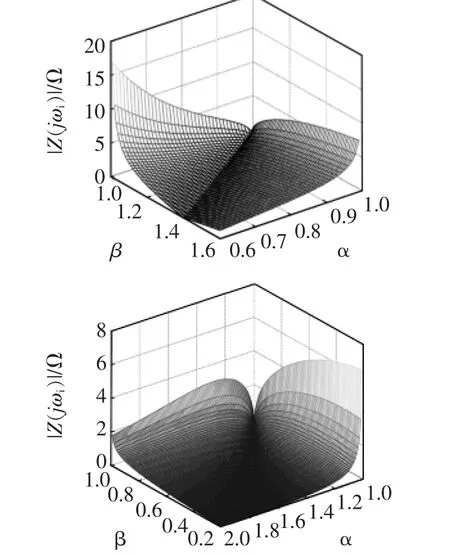
图5 |Z（jωi）|与α、β的关系曲线Fig.5 3-D view of|Z（jωi）|under different α and β

2.2 相位特性

由上述分析可知，当ω=ωr即电路表现纯实部阻抗特性时，φ（ω）=0；当 ω=ωr即电路表现纯虚部阻抗特性时，φ（ω）=±π/2。 一般情况下，根据方程（6），可以得到分数阶LβCα串联电路的相位特性曲线，如图6所示。

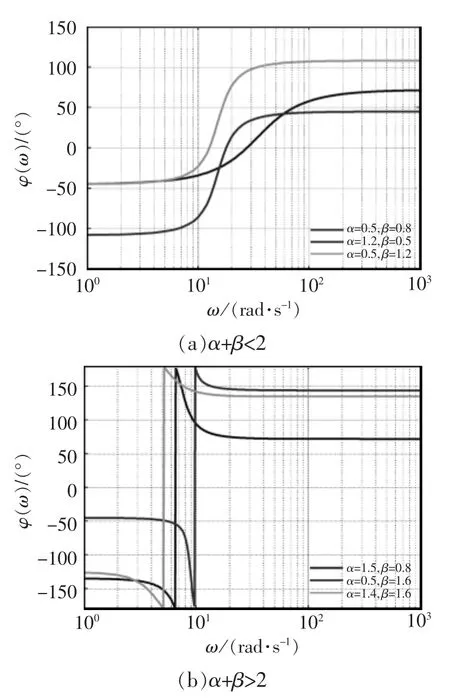
图6 相位特性曲线Fig.6 Phase characteristic curves

由图6可知，当α+β＜2时，随着ω的变化，φ（ω）的变化是连续的，且由-απ/2变化到βπ/2；当α+β＞2 时，φ（ω）同样由-απ/2 变化到 βπ/2，但变化是不连续的，在 ω=ωr时 φ（ω）发生了跳变。

3 分数阶互感及变压器模型的特性分析

3.1 电路模型

从上述分析可知，在分数阶情况下，电感电容分别增加了阶次α、β，其阻抗与α、β有关，因此相比于整数阶情况来说，分数阶LβCα电路呈现出更加丰富的阻抗特性。运用第2节阻抗分析方法来研究分数阶互感及变压器模型的阻抗特性。

分数阶互感及变压器模型的基本拓扑如图7所示，其中原边电感和副边电感的阶数分别为α和β，互感阶数为γ。其等效电路模型如图8所示。

图7 分数阶互感及变压器模型Fig.7 Model of fractional-order mutual inductance and transformer

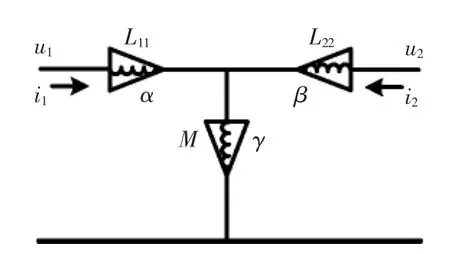
图8 等效电路模型Fig.8 Model of equivalent circuit

由图8可得分数阶互感电路阻抗矩阵方程为

令 s=jω，则可得

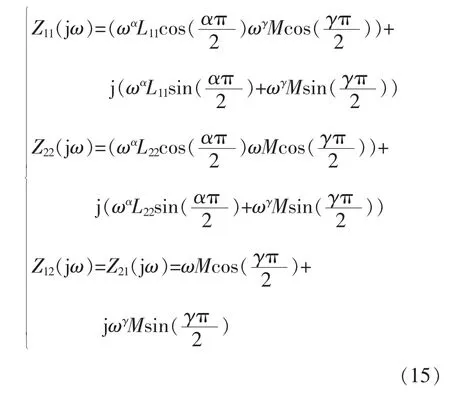
3.2 阻抗特性和相位特性

由式（6）由可知，分数阶互感及变压器模型的阻抗矩阵与 α、β、γ 有关，为简化分析，令 α=β，讨论α、β、γ不同取值下的分数阶互感及变压器模型的阻抗特性和相位特性。

当 α=β=γ时，阻抗矩阵可转化为

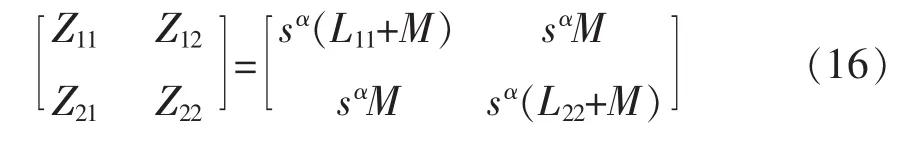
由式（16）可知，阻抗矩阵是对称矩阵，因此分数阶互感电路也是对称的。此时所有阻抗矩阵元素的相角均为απ/2，只与阶数α有关。特别地，当α=β=γ=1时，阻抗矩阵的所有元素实部均为0，相角均为π/2，表现出纯感性。

当α=β≠γ时， 易知Z12和Z21的相角为 γπ/2，Z11和 Z22的相角 φ11,22（ω）可根据方程（6）计算。 图 9所示为 ω=1 rad/s和 ω=10 krad/s时，φ11,22（ω）与 α（β）、γ之间的关系。

由图 9 可知，当 ω 一定时，在 0＜α（β）＜2 且 0＜γ＜2 的范围内，随着 α（β）、γ 的增大，φ11,22（ω）也增大。由图像的对称性可以看出，自感阶数α（β）和互感阶数γ对φ11,22（ω）的影响是一致的。对比图9可知，而当 α（β）、γ、一定时，随着 ω 的增大，φ11,22（ω）也增大。

令方程（15）中 Z11、Z22的虚部为 0，即

可得频率和阻抗分别为

图9 Z11、Z22的相位特性三维关系Fig.9 3-D view of phase characteristics of Z11and Z22

此时自阻抗Z11、Z22表现出纯实部特性。ω=1 rad/s和 ω=10 krad/s两种条件下，γ与 α（β）之间的关系曲线如图10所示。由图中可以看出，当Z12、Z21表现出纯实部特性，0＜α（β）＜2、 0＜γ＜2 无法同时满足，因此实际情况是无解的。

令式（15）中 Z12、Z21的实部为 0，即

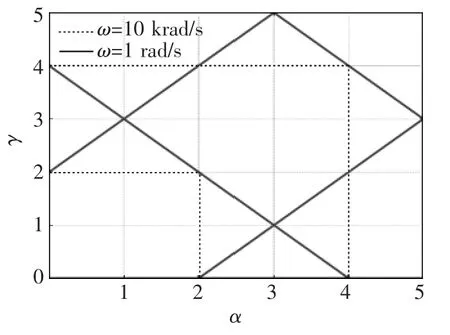
图10 纯实部特性下的γ-α（β）关系曲线Fig.10 γ-α（β） curves under the pure real impedance characteristic

可得频率和阻抗分别为

此时自阻抗Z11、Z22表现出纯虚部特性。给定α（β）与ω，便可以确定 γ。 如图11、图 12所示分别为 ω=1 rad/s和 ω=10 krad/s情况下， γ、Z11，22（jω）与α（β）的关系曲线。 特别地，当 α=β=γ=1 时，阻抗幅值取得最大值。

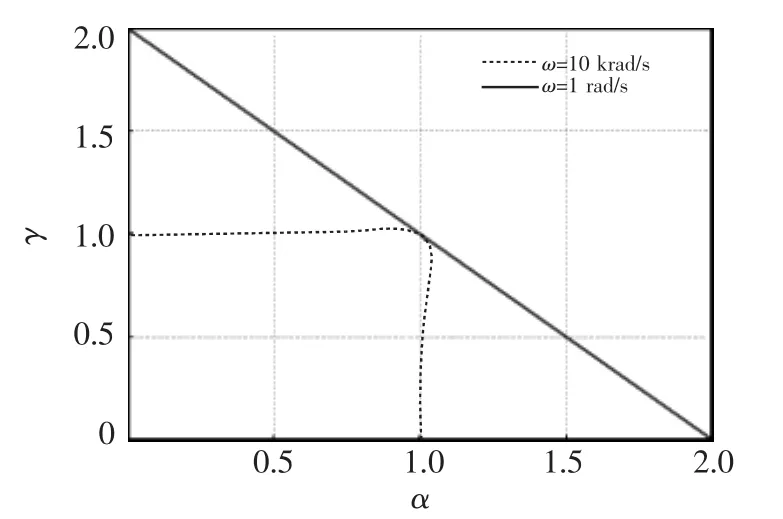
图11 纯虚部特性下的γ-α（β）关系曲线Fig.11 γ-α（β） curves under the imaginary impedance characteristic

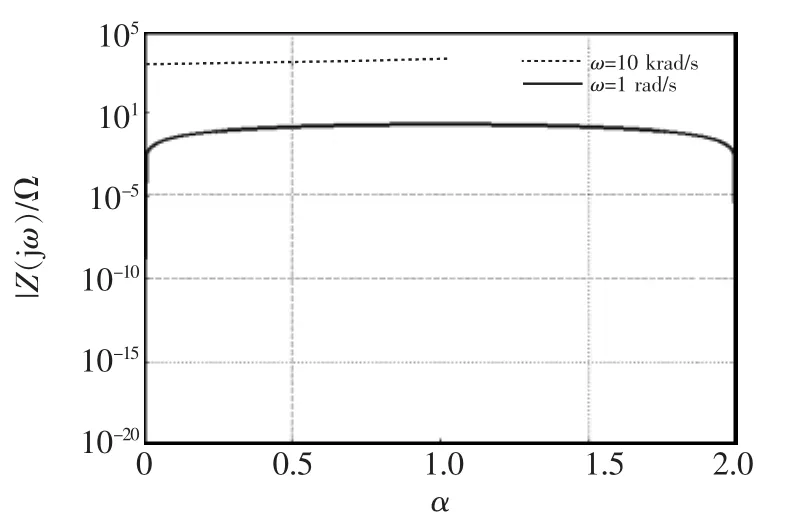
图12 Z11,22与α（β）的关系曲线Fig.12 Z11,22-α（β） curves under different ω

4 结语

本文在分析传统分数阶LβCα电路 （以串联为例）阻抗特性的基础上，研究了分数阶互感电路及变压器模型的阻抗特性，分析了阻抗矩阵在不同阶数下的相位特性，以及分数阶条件下特有的纯实部特性和纯虚部特性。研究表明，自感阶数和互感阶数对阻抗相位的影响是一致的。当自感阶数和互感阶数在0～2之间取值时，自阻抗只可能表现出纯虚部特性而不能表现出纯实部特性。给定自感阶数和角频率，便可以确定互感阶数。最后给出了纯虚部阻抗特性下，阻抗频率、幅值与电感阶数的关系曲线。由于分数阶互感电路及变压器模型的电路参数增加了自感和互感的阶数，因此设计自由度更高，应用范围更广。本方法将对分数阶无线电能传输系统具有一定的指导作用。

[1]Engheta N.On the role of fractional calcus in electro-magnetic theory[J].IEEE Antennas and Propagation Ma-gazine,1997,39（4）：35-46.

[2]Radwan A G,Elwakil A S，Soliman A M.Fractional-order sinusoidal oscillators：design procedure and practical examples[J].IEEE Transactions on Circuit and Systems,2008,55（7）：2051-2063.

[3]Li Chunlai,Yu Simin,Luo Xiaoshu.Fractional-order permanent magnet synchronous motor and its adaptive chaotic control[J].Chin.Phys.B,2012,21（10）：15-21.

[4]Pires E J,Machado J A,Oliveira P B.Fractional order dynamics in a GA planner[J].Signal Processing,2003,83（11）2377-2386.

[5]Battaglia J,Cois O,Puigsegur L,et al.Solving an inverse heat conduction problem using a non-integer identified model[J].International Journal of Heat and Mass Transfer,2001,44（14）：2671-2680.

[6]El-Sayed A M A,Nour H M,Raslan W M,et al.Fractional parallel RLC circuit[J].Alexandria Journal of Mathematics,2012,3（1）：11-23.

[7]Diao Lijie,Zhang Xiaofei,Chen Diyi.Fractioanl-order multiple RLαCβcircuit[J].Acta Phys.Sin.,2014,63（3）：1-13.

[8]Radwan A G.Resonance and quality factor of the RLαCαfractional circuit[J].IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2013,3（3）：377-384.

[9]Radwan A G,Salama K N.Passive and active elements using fractional passive and active elements using LβCαcircuit[J].IEEE Transactions on Circuits and Systems,2011,58（10）：2388-2397.

[10]王国东，原璐璐，王允建.磁耦合谐振式无线电能传输系统的四线圈模型研究[J]. 电源学报，2015，13（1）：101-106.

Wang Guodong,Yuan Lulu,Wang Yunjian.Research on the four coil model of magnetically-coupled resonant wireless power transmission systems[J].Journal of Power Supply,2015,13（1）：101-106（in Chinese）.

[11]王振亚，王学梅，张波，等.电动汽车无线充电技术的研究进展[J]， 电源学报， 2014,12（3）：27-32.

Wang Zhenya,Wang Xuemei,Zhang Bo,et al.Advances of wireless charging technology in electric vehicle[J].Journal of Power Supply,2014,12（3）：27-32（in Chinese）.

[12]Ma Long,Liang Guishu,Dong Huaying.Sensitivity analysis of the networks with fractional order reactance[J].Journal of North China Electric Power University,2013,40（3）：6-10.

[13]Soltan A,Radwan A G,Soliman A M.Fractional-order mutual inductance：analysis and design[J].Int.J.Circ.Theor.Appl.,2016,44（1）：85-97.

Analysis of Fractional-order Mutual Inductance and Transformer Model

LIU Xiao,ZHANG Bo,XIE Fan,QIU Dongyuan
（School of Electrical Power,South China University of Technology,Guangzhou 510640,China）

Fractional characteristic analysis of magnetic coupling or electrical energy conversion has been involved in few researches.In this paper,the fractional-order mutual inductance and transformer model is analyzed.First,impedance analysis of a fractional LC circuit is introduced as an example.Then,the same method is applied to analyze the impedance matrix characteristics of the fractional-order mutual inductance and transformer model.The impedance frequencies that satisfy the pure real impedance and the pure imaginary impedance under fractional conditions are obtained.As a result,phase characteristics as well as relationships among impedance frequencies,amplitudes and inductor orders under different impedance characteristics are illustrated.The fractional orders of self-inductance and mutual-inductance increase the degree of freedom for model design which means more generality.

fractional order;mutual inductance;transformer model;impedance characteristics

刘潇

刘潇（1990-），男，硕士研究生，研究方向：电力电子系统分析与控制，E-mail：rayshawn1220@163.com。

张波（1962-），男，通信作者，教授，博士生导师，研究方向：电力电子与电力传动，E-mail：epbzhang@scut.edu.cn。

谢帆（1985-），男，博士，研究方向：电力电子与电力传动，E-mail：epfxie@scut.edu.cn。

丘东元（1972-），女，博士，教授，研究方向：电力电子与电力传动，E-mail：epd yqiu@scut.edu.cn。

10.13234/j.issn.2095-2805.2017.4.143

TM40

A

2015-12-08

国家自然科学基金重点项目资助（51437005）

Project Supported by the Key Program of the National Natural Science of China（51437005）