三相SPWM调制时的谐波相序及“零序”谐波流动

齐元瑞，肖国春，卢 勇，卢大鹏，郑家禄

（西安交通大学电气工程学院，西安 710049）

三相SPWM调制时的谐波相序及“零序”谐波流动

齐元瑞，肖国春，卢 勇，卢大鹏，郑家禄

（西安交通大学电气工程学院，西安 710049）

对于三相逆变电路中广泛采用的共用一个载波的三相正弦脉冲宽度调制（SPWM），当载波比不是3的整数倍数时，会出现“零序”（3k次）谐波电流的流动。“零序”谐波具有对称性，其相序有可能为正，也有可能为负，且传统概念上谐波的正序变为了负序，而谐波的负序变为了正序。这些现象对于三相系统的正常运行将带来不利影响。为此，对共用一个载波的三相SPWM调制在不同载波比时的谐波相序特性及“零序”（3k次）谐波电流流动现象进行了深入分析，为三相SPWM的调制方法应用提供了依据。理论、仿真和实验验证了分析方法和结论的正确性。

SPWM；谐波相序；零序谐波；同载波调制

在三相三线制系统中，传统概念认为3k（k为正整数）次谐波为零序谐波，3k+1次谐波为正序谐波，3k-1谐波为负序谐波，且由于没有流通回路，因此不会存在零序（3k次）谐波电流的流动。然而，在三相正弦电压（或电流）逆变电路中，广泛采用的共用一个载波的三相正弦脉冲宽度调制SPWM（si-nusoidal pulse width modulation）技术[1]中，当载波比不是3的整数倍时，这种调制就成为不对称调制，则三相三线系统中就会出现“零序”谐波电流的流动，并且传统正、负序概念也发生了变化。

三相SPWM不对称调制时会出现“零序”谐波，“零序”谐波电流流动具有对称性和平衡性，其相序有可能为正也有可能为负；而且，在这种情况下，传统概念上为正序的谐波变为了负序，负序的谐波变为了正序。这些特性对于三相系统的正常运行将带来不利影响，特别是当载波频率比较低时这个问题更加突出。虽然SPWM调制技术的研究和应用已有40多年的历史[2-5]，但有关三相SPWM不对称调制时的谐波相序及“零序”谐波等问题还未得到充分认识。文献[6-7]给出了逆变器输出电压频谱的几种不同分析方法；文献[8]分析了开关（载波）频率两侧谐波的相序及相互作用，但未提到零序（3k次）谐波相序的问题；文献[9]中提到了开关频率附近会存在“奇怪”的“零序”（3k次）谐波的问题，但对谐波相序和“零序”谐波出现的规律未做进一步系统分析。由于载波频率附近的谐波分量对三相逆变电路系统的性能影响最大，所以，如何选取载波频率，如何减少载波频率附近的谐波分量及其对系统的影响，就成为提高三相SPWM调制性能的关键。

本文对共用一个载波的三相SPWM调制时，载波比分别为基波的3m、3m+1、3m+2倍时（m为正整数）的谐波的相序特性及“零序”（3k次）谐波电流流动现象进行了详细分析，为三相SPWM调制方法应用提供了依据。理论、仿真和实验验证了分析方法和结论的正确性。

1单相半桥逆变电路谐波分析

单相半桥逆变电路如图1所示，加在负载两端的只有Ed和-Ed两种电平。当采用自然采样的SPWM时，其调制原理及调制波形如图2所示。信号波幅值小于载波幅值输出-Ed，信号波幅值大于载波幅值输出Ed。实际应用的SPWM都为异步调制，它在信号波的各周期内包含的脉冲模式没有重复性，因此以载波角频率ωs为基准分析其谐波分布及相序情况[1]。

图1 单相半桥逆变电路Fig.1 Single-phase half-bridge inverter circuit

设调制信号为

式中：ω为调制波角频率；a为调制度；φ为初相角。由文献[1]可知交流侧输出电压中含有的谐波分量。

（1）当 n=1,3,5，…、k=2,4,6，…时，有

式中：J0为0阶贝塞尔函数;Jk为k阶贝塞尔函数。

（2）当 n=2,4,6，…、k=1,3,5，…时，有

由式（2）、式（3）可知，SPWM 的调制谐波主要分布在载波（开关）频率及载波频率的整数倍附近。如果载波频率较低，载波频率附近的谐波将对系统的输出波形有很大影响。

图2 自然采样的SPWM调制波形Fig.2 SPWM modulation waveform of the natural sample

2 三相桥式逆变电路谐波分析

三相桥式逆变电路如图3所示，其各相相对于直流电源中点的相电压和单相半桥逆变电路相同。所以，三相桥式逆变电路可以按单相半桥逆变电路来分析。

图3 三相桥式逆变器Fig.3 Three-phase inverter

设三相对称系统的调制波信号为

根据单相输出相电压谐波含量的表达式，可以得到各相相对于电源中点N'的相电压谐波表达式。

2.1 当 n=1，3，5，…、k=2，4，6，…时，各相电压的谐波推导

由式（2）及式（4）～式（6）可得，A 相相电压谐波含量为

B相相电压谐波含量为

C相相电压谐波含量为

在三相对称电路中，电源中点和负载中点之间的谐波含量FNN'为

由式（7）～式（10）可以得到各相相电压中所含谐波分别为

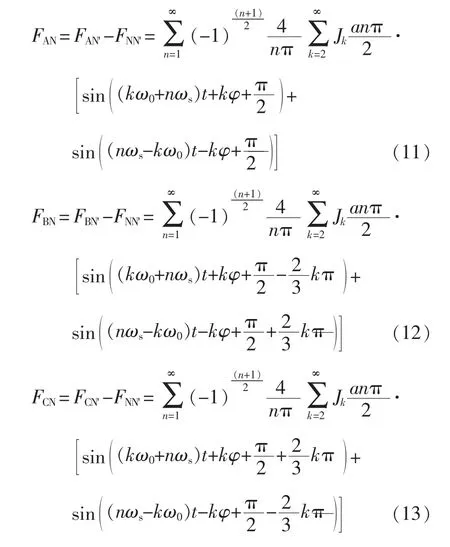
2.2 当 n=2，4，6，…、k=1，3，5，…时，各相电压谐波推导

由式（3）～式（6）可得，A 相相电压谐波含量为

B相相电压谐波含量为

C相相电压谐波含量为

在三相对称电路中，电源中点和负载中点之间的谐波含量FNN'为

由式（14）～式（17）可以得到各相相电压中所含谐波分别为

对比式（11）～式（13）与式（18）可以看出，以上两种情况各相相电压谐波的相位变化是相同的。

2.3 谐波相序分析

从上面各相相电压的谐波分析可以看出，共用一个载波的三相SPWM调制时，各相相电压中所含谐波次数为 nωs±kω0。nωs+kω0次谐波的三相相位差分别为 0，-2kπ/3，2kπ/3； nωs-kω0次谐波的三相相位差分别为 0，2kπ/3，-2kπ/3。对比三相谐波的相位变化，就可以得到各次谐波的相序特性，并能进一步分析总结其相序变化的规律。

开关过程产生的谐波主要分布在载波（开关）频率附近，以载波频率及其倍频呈对称分布，并朝频率增加和减少的方向逐渐衰减。一般载波频率比信号波频率高很多，载波频率附近的谐波对系统影响最大，所以，这里取 n=1，对 nωs±kω0次谐波的相序特性进行分析。

（1）当 k=6L+2（L=0，1，2，…）时，ωs-kω0次谐波为正相序,ωs-kω0= ［3（m-2L-1）＋1］ω0次谐波的传统相序也为正相序；ωs+kω0次谐波为负相序,ωs+kω0=［3（m+2L+1）－1］ω0次谐波的传统相序也为负相序。

（2）当 k=6L-2（L=1，2，3，…）时，ωs-kω0次谐波为负相序,ωs-kω0= ［3（m-2L-1）-1］ω0次谐波的传统相序也为负相序；ωs+kω0次谐波为正相序,ωs+kω0=［3（m+2L－1）+1］ω0次谐波的传统相序也为正相序。

2.3.2 载波比H=3m＋1（m=1，2，3，…）

（1）当 k=6L+2（L=0，1，2，…）时，ωs-kω0次谐波为正相序,ωs-kω0= ［3（m-2L）-1］ω0次谐波的传统相序却为负相序；ωs＋kω0次谐波为负相序,ωs＋kω0=［3（m＋2L＋1）］ω0次谐波的传统相序却为零相序。

（2）当 k=6L－2（L=1，2，3，…）时，ωs-kω0次谐波为负相序,ωs-kω0= ［3（m-2L＋1）］ω0次谐波的传统相序却为零相序；ωs＋kω0次谐波为正相序,ωs＋kω0=［3（m＋2L）－1］ω0次谐波的传统相序却为负相序。

例如，当载波比为40时，其三相谐波相序分布如图4所示。图中，谐波分量最大的是38次和42次（k=2），38次呈现正相序，42次是负相序；谐波分量较大的是36次和44次（k=4），36次呈现负相序，44次是正相序。

图4 载波比为40的谐波相序Fig.4 Harmonic phase sequence when the carrier ratio=40

2.3.3 载波比H=3m+2（m=1，2，3，…）

（1）当 k=6L+2（L=0，1，2，…）时，ωs-kω0次谐波为正相序,而 ωs-kω0=［3（m-2L）］ω0次谐波的传统相序却为零相序；ωs＋kω0次谐波为负相序,而 ωs＋kω0=［3（m＋2L+1）+1］ω0次谐波的传统相序却为正相序。

（2）当 k=6L－2（L=1，2，3，…）时，ωs-kω0次谐波为负相序,而 ωs-kω0=［3（m-2L+1）＋1］ω0次谐波的传统相序却为正相序；ωs+kω0次谐波为正相序,而ωs+kω0=［3（m+2L）］ω0次谐波的传统相序却为零相序。

例如，当载波比为41时，其谐波相序分布如图5所示。图中，谐波分量最大的是39次和43次（k=2），39次为正相序，43次是负相序；谐波分量较大的是37次和 45次（k=4），37次是负相序，而45次呈现正相序。

图5 载波比为41的谐波相序Fig.5 Harmonic phase sequence when the carrier ratio=41

由以上分析可知，当载波比是3的整数倍时，其谐波相序与其传统相序是一致的。在载波频率附近（n=1），当载波比为 3m+1 时，其“零序”（3k 次）谐波的相序为负序，3k+2次谐波的相序为正序；当载波比为3m+2时，其“零序”（3k次）谐波的相序为正序，3k-2次谐波的相序为负序。所以，当载波比为3m+1，3m+2时逆变器输出的谐波相序与它传统相序不一致，这就导致了“零序”谐波电流在三相三线制系统中流通的现象，且其他谐波的相序也与其传统相序不一致。

3 仿真及实验验证

对如图3所示的三相桥式逆变电路进行仿真。负载为Y型连接的阻感负载（L=4 mH,R=25Ω），调制波频率为50 Hz，开关频率为2 kHz，载波比为40。其仿真输出三相电流波形如图6所示。其中，A相电流的FFT分析结果如图7所示，38次、42次谐波的相位分别如图8和图9所示。从仿真结果可以看出，交流侧相电流中主要含有38次、42次谐波，且38次谐波相序为正序，42次谐波相序是负序。仿真研究验证了以上理论分析的正确性。

图6 输出相电流波形Fig.6 Phase currents waveforms

按如图3所示主电路进行实验，负载为三相对称阻感负载，实验参数与仿真参数一致，其中L=4 mH，R=25 Ω，开关频率取 2 kHz（载波比为 40），实验记录仪器为HIOKI 3196电能质量分析仪。

图7 A相电流FFT分析Fig.7 FFT analysis of phase A current

图8 38次谐波的相位Fig.8 Phases of 38th harmonic

图9 42次谐波的相位Fig.9 Phases of 42nd harmonic

图10 三相相电流波形Fig.10 Waveforms of three-phase currents

表1 50次以内的A相谐波幅值Tab.1 Harmonic amplitudes of phase A within 50th harmonic

三相电流实验波形如图10所示。对A相作FFT分析可以得到50次以内的谐波幅值，如表1所示。从表1中可以看出，开关（载波）频率附近的谐波含量比较大，特别是38次、42次谐波含量超过10%。三相电流的相位分析结果分别如图11和图 12 所示，图中，U1、U2、U3为三相电网电压，主要作为相位测试的参考；I1、I2、I3为逆变器输出三相相电流。由于电网中38次、42次电压谐波含量极少，未达到测试仪器测试范围，其谐波电压相位的测试没有意义，可以忽略，而谐波电流相位的测试是可以参考的。测试表明，38次谐波的相序为正相序，42次谐波的相序为负相序。实验证明了理论和仿真分析结论的正确性。

图11 38次谐波电流相位Fig.11 Phasess of 38th harmonic currents

图12 42次谐波电流相位Fig.12 Phasess of 42nd harmonic currents

4 结论

（1）共用一个载波的三相SPWM调制时，nωs+kω0次谐波的三相相位差分别为 0、-2kπ/3和 2kπ/3；nωs-kω0次谐波的三相相位差分别为 0，2kπ/3和-2 kπ/3。当载波比不是3的整数倍数时，系统中会出现“零序”谐波电流的流动，谐波相序的分布仍然是正、负序相间的。

（2）在载波频率附近（n=1），当载波比是3的整数倍（3m）时，其谐波相序与其传统的相序是一致的，不存在“零序”（3k次）谐波电流流动；当载波比为3m+1时，其“零序”（3k次）谐波的相序为负序，3k+2次谐波的相序为正序；当载波比为3m+2时，其“零序”（3k 次）谐波的相序为正序，3k－2 次谐波的相序为负序。理论、仿真和实验验证了分析方法和结论的正确性。

[1]日本电气学会电力半导体变流方式调研专门委员会.电力半导体变流电路[M].王兆安,张良金,译.北京：机械工业出版社,1993.

[2]Bowes S R,Holliday D,Grewal S.Regular-sampled harmonic elimination PWM control of single-phase two-level inverters[J].Electric Power Applications,IEE Proceedings,2001,148（4）：309-314.

[3]贺昱曜,李宏,何华.一种新型软化SPWM波形合成方法及谐波分析[J].中国电机工程学报.2002,22（12）：118-122.

He Yuyao,Li Hong,He Hua.A novel soft SPWM waveform synthetic method and harmonic analysis[J].Proceedings of the CSEE,2002,22（12）：118-122（in Chinese）.

[4]费万民,都小利,居荣,等.基于等面积法的多电平逆变器SPWM方法[J].电工技术学报,2010,25（3）：89-96.

Fei Wanmin,Du Xiaoli,Ju Rong,et al.A novel PWM method for multilevel inverters[J].Transactions of China Electrotechnical Society.2010,25（3）：89-96（in Chinese）.

[5]Hava A M,Cetin N O.A generalized scalar PWM approach with easy implementation features for three-phase three-wirevoltage-source inverters[J].IEEE Transactions on Power Electronics,2011,26（5）：1385-1395.

[6]Holmes D G.A general analytical method for determining the theoretical harmonic components of carrier based PWM strategies[C].the 1998 IEEE Thirty-Third IAS Annual Meeting,1998,2：1207-1214.

[7]Odavic M,Sumner M,Zanchetta P,et al.A theoretical analysis of the harmonic content of PWM waveforms for multiple-frequency modulators[J].IEEE Transactions on Power Electronics,2010,25（1）：131-141.

[8]Grant T L,Barton T H.Control strategies for PWM drives[J].IEEE Transactions on Industry Applications,1980,IA-16（2）：211-216.

[9]Hamman J,Van Der Merwe F S.Voltage harmonics generated by voltage-fed inverters using PWM natural sampling[J].IEEE Transactions on Power Electronics,1988,3（1）：297-302.

Harmonic Phase Sequence and “Zero Sequence” Harmonics Flowing in Three-phase SPWM

QI Yuanrui， XIAO Guochun， LU Yong， LU Dapeng， ZHENG Jialu
（School of Electrical Engineering,Xi’an Jiaotong University,Xi’an 710049,China）

Single-phase carrier modulation is widely used in three-phase inverter systems.Zero sequence harmonics exists in such systems when the carrier ratio is not the multiple of 3.In this case,the phase sequence of these“zero sequence harmonics”can be either positive or negative,and the harmonics phase sequence which traditionally considered as positive turn to be negative and vice versa.The phenomena will affect the normal operation of three-phase inverter systems to some extent.Therefore,in this paper,the characteristics of harmonics phase sequence and“zero sequence”harmonics current flowing are comprehensively analyzed in the same carrier of three-phase SPWM modulation to provide a theoretical basis for application of single-phase modulation scheme.Theoretical,simulation and experimental results demonstrate and confirm the analysis method and its conclusions.

sinusoidal pulse width modulation（SPWM）;harmonics phase sequence;zero sequence harmonics;singlecarrier modulation

齐元瑞

齐元瑞（1988-），男，硕士研究生，研究方向：电能质量治理，E-mail：547253480@qq.com。

肖国春（1965-），男，博士，博士生导师，研究方向：电能质量分析与控制技术，电力电子系统的建模、仿真与控制，分布式发电技术，电力电子装置设计及应用，E-mail：xgc@mail.xjtu.edu.cn。

卢勇（1987-），男，博士研究生，研究方向：电能质量治理，E-mail：286649045@qq.com。

卢大鹏（1989-），男，硕士研究生，研究方向：电能质量治理，E-mail：525199091@qq.com。

郑家禄（1990-），男，通信作者，硕士研究生，研究方向：微网控制，E-mail：zjl30 02@stu.xjtu.edu.cn。

10.13234/j.issn.2095-2805.2017.4.41

TM464

A

2015-12-07

国家自然科学基金资助项目（51277146）

Project Supported by National Natural Science Foundation of China（51277146）