基于多目标优化算法的IPT系统谐振网络参数设计
黄永灿,戴 欣,邹 洋
(重庆大学自动化学院,重庆400044)
基于多目标优化算法的IPT系统谐振网络参数设计
黄永灿,戴 欣,邹 洋
(重庆大学自动化学院,重庆400044)
传统IPT系统的谐振网络参数设计方法存在着低效、准确性差以及难以对具有多个设计目标的系统进行谐振网络参数设计等缺陷。首先提出了一种基于NSGA-II多目标优化算法的谐振网络参数的设计方法,经一次运算即可得到多组满足系统设计目标的谐振网络参数值,克服了传统谐振网络参数设计方法的缺陷。以PP结构的IPT系统为例,把高电压增益和系统效率最优设计作为目标,设计出了最优谐振网络参数。仿真和实验结果表明,设计出的谐振网络参数能够满足系统需要。
NSGA-II;电流型IPT系统;遗传算法;参数配置
感应耦合电能传输技术是一种利用电磁场实现电能以非接触方式进行传输的新兴技术。因为该技术可以提高用电设备的灵活性与可靠性,近年来受到研究者的普遍关注。该技术目前已经在电动汽车、数码家电及复杂工业环境等领域得到了广泛的应用。
在感应耦合电能传输系统中,系统谐振网络参数对于系统的可靠性与稳定运行有着重要意义。然而,由于实际系统中普遍存在会使系统阶数过高的多级谐振环节和多个设计目标(如电压增益、输出功率以及效率等),会导致参数设计变得繁琐且复杂。因此,在传统的参数设计中,通常采用经验法与试错法进行谐振网络参数配置。这两种方法均存在效率低下、目标性不明确等缺陷,会造成时间与财力上的极大浪费。
针对这一问题,本文基于NSGA-II(non-dominated sorting genetic algorithms-II)多目标遗传算法,提出一种面向多个设计目标的感应电能传输系统谐振网络参数的设计方法,并给出了算法的具体设计步骤,通过对实际系统进行仿真与实验,验证了该方法的有效性。
1 传统谐振网络参数配置方法
1.1 传统谐振网络参数配置方法
传统IPT系统谐振网络参数配置方法适用面广,一般的IPT系统谐振网络参数配置问题都可以使用传统的参数配置方法解决。传统谐振网络参数配置方法的核心思维是利用以往的配置经验假设参数值以及参数范围,达到降维简化分析的目的。通过对IPT系统的部分参数进行假定,使系统研究参数和系统配置目标之间的关系更简单直接。其参数配置步骤如下:
步骤1 建立IPT系统的数学模型。目的不同,建立的模型类型也不同,一般为了分析IPT系统的稳态,建立的模型都是正弦交流阻抗模型。
步骤2根据系统的数学模型和性能目标得到目标的函数表达式,选定需要配置的谐振网络参数。
步骤3选取一个需要配置的参数,依靠经验确定其大致范围,同时对其他参数进行假定。
步骤4在选定范围内变化配置参数,再确定一个比较合理的值(此值可能不会使得系统性能直接满足要求,但可以使得系统性能进一步接近目标)。
步骤5逐个选定其余参数进行配置。当配置完所有待配参数之后,若系统性能达到目标要求,那么这组参数就是可以使用的合格参数;否则重复步骤3~步骤5,直到满足系统的目标和要求。
传统谐振网络参数配置方法的本质是重复实验和机械化操作。经过近几年来的发展,IPT系统的谐振网络参数配置方法有了其他类型,如同时配置2个参数(得到的结果是三维图)[1]以及对系统目标函数进行其他方式的简化等,但其本质上也属于传统谐振网络参数配置方法。
1.2 传统谐振网络参数配置方法的缺点
传统方法的缺点主要有以下几点:
(1)没有考虑参数之间的相互影响;
(2)有一定的盲目性,需要靠以往系统谐振网络参数配置经验进行其余参数的假定;
(3)效率低,为了寻找到合适的参数,常常需要进行大量的重复实验;
(4)难以对具有多个目标和要求的IPT系统进行有效的参数配置;
(5)模型的准确性偏低,因为计算效率低,为了便于计算,需要对目标公式进行化简。
传统的谐振网络参数配置方法的主要缺点是依赖以往系统参数配置的经验,使谐振网络参数配置具有一定的盲目性。本文提出了使用NSGA-II多目标遗传算法对IPT进行谐振网络参数配置,可以克服传统方法的缺陷,跳出传统参数配置方法的核心思维定势,高效、快速、准确地对IPT系统进行参数配置。
2 IPT系统谐振网络参数多目标优化设计算法
2.1 多目标优化问题和遗传算法
在实际的工程中,常常会碰到多个优化准则和预期目标的问题,这些问题的预期目标和优化准则之间往往是相悖的,称之为多目标优化问题。多目标优化问题的最优解一般为一个解集,这个解集里面的解被称为帕略特最优解。
多目标优化问题通常可表示为

式中:fm(x)为多目标问题中待优化目标的函数;gj(x)为不等式约束条件;hk(x)为等式约束条件;x为系统的待优化变量。
遗传算法是仿生算法的一种,它是一种模拟生物进化过程的选择和遗传机理的计算模型。作为当代的三大非经典最优化理论算法之一,遗传算法它是一种随机算法,有着不依赖问题内在特性的优点,有很强的全局搜索能力。但传统的遗传算法有着对选择、交叉和变异算子的参数依赖性强,搜索速度慢等等问题。
针对多目标优化问题,Deb K在2002年提出了一种新型的多目标优化算法—NSGA-II[2]。NSGA-II采用了快速非支配排序、精英保留策略以及基于密集度算子和非劣等级的锦标赛选择算子,使得算法能够快速地找到全局最优解,且算法得到的帕略特最优解会均匀地分布在整个帕略特最优前沿上。与传统的NSGA算法相比[3],NSGA-II具有时间复杂度小、搜索速度快、不需要设置共享参数就能保证解的多样性等等一系列优点。经典多目标问题的对比测试发现,NSGA-II算法在解的分布和逼近真正的帕略特最优解附近的收敛性都要优于Paretoarchived evolution strategy EA和strength-Pareto EA这两种常用的遗传算法。
2.2 NSGA-II算法的运算流程
NSGA-II算法解决多目标优化问题的流程如图1所示。
(1)产生目标函数 fm(x)和限制函数 gj(x)、hk(x)。
(2)随机产生个体数量为N的初始化种群Pt。
(3)对种群中的每个个体进行快速非支配排序并且计算其密集度。
(4)对种群Pt进行拥挤度锦标赛选择,交叉以及变异等操作,得到子代Qt。

图1 NSGA-II算法流程Fig.1 Flow chart of NSGA-II algorithm
(5)将父代和子代重组为一个种群Rt,进行快速非支配排序并计算密集度。
(6)通过精英选取策略对Rt进行筛选得到个体数为N的新父代Pt+1。
(7)检查是否满足停止条件。满足则停止,不满足则重复第(3)~(7)步。
因为精英保留策略的存在,NSGA-II算法解决多目标问题的流程在第1代时会稍有不同。
2.3 NSGA-II算法配置谐振网络参数
NSGA-II有很强的全局搜索能力,使用NSGAII算法进行参数配置可以避开传统方法的众多缺点。NSGA-II算法谐振网络参数配置步骤以下:
(1)对需要进行谐振参数配置的IPT系统建模。
(2)明确模型的目标函数、限制函数、待优化参数及其范围。
(3)使用NSGA-II对IPT系统进行谐振网络参数优化设计。
(4)根据实际的系统目标和条件,对NSGA-II优化得到帕略特解集进行决策选择,选出最满意的解,并且整理出理想参数。
(5)根据实际条件对理想参数进行整理得到相应的实际参数。需要指出的是,在上面NSGA-II算法进行IPT系统参数配置的第5步中,理想参数是指NSGA-II直接运算取得的参数,它具有一定的理想性,在现实的条件下难以得到和其完全一样的参数。实际参数是指实际系统中使用的尽量接近理想参数的谐振网络参数。
3 PP结构IPT系统的参数配置
3.1 高增益和高效率的PP结构IPT系统
太阳能电池板有着携带方便并且体积小等优点,结合IPT系统可以在户外复杂的环境下方便地实现用电设备的无线供能。通常小型的太阳能电池板输出的电压不高,为了保证供电设备的使用,必须要对其进行升压。IPT系统除了作为无线电能传输技术之外本身也可以进行升压,因此结合IPT系统的太阳能电池板可以不需要额外的变压器就能实现无线电能传输和输出电压提升。本文对PP结构(即原、副边均采用并联谐振补偿)的IPT系统进行谐振网络参数配置,预期的系统电压增益目标设为1.5,功率传输效率目标为75%。
3.2 PP结构IPT系统交流阻抗建模
建立PP结构数学模型IPT系统电路如图2所示[4],建模参数定义如下:
Vi和Ii分别为输入谐振网络的电压和电流的有效值;ω为系统工作的固定谐振频率;Ro为系统的负载;k和M分别为原边和副边耦合的耦合系数以及互感;Lp、Cp和Rp分别为谐振网络中的原边耦合电感、原边补偿电容以及原边电感的串联等效损耗电阻;Ls、Cs和Rs分别为谐振网络中的副边耦合电感、副边补偿电容以及副边电感的串联等效损耗电阻;Ip和Is分别为系统工作在稳态时的原副边电感中流过的电流的有效值;Vp和Vs分别为原、副边的互感电压的有效值;I为高频逆变输出端等效电流源的电流;Rn为系统中线阻;R'为整流桥侧的实际额定负载。

图2 PP结构的IPT系统电路Fig.2 Circuit of PP topology
利用互感模型,副边互感电压为

副边等效阻抗为

由式(2)、式(3)可以得到 Ls中的电流为

考虑互感效应,原边的互感电压为

则反射回Ls的阻抗Zr为

再对原边进行阻抗分析可以得到

式中,Z为电路的总阻抗。
PP结构IPT系统输入谐振网络的方波电流幅值I'和输入高频逆变器部分的电压Vi之间的关系[5]为

式中:L为和输入电压端串联的大电感,取值范围为2~10 mH;Z为其后面连接的电路的总阻抗。根据式(8)可以求出输入方波电流的幅值。
对谐振电路来说,谐波分量对输出电压和功率的影响都比较小,因此可以对I'进行傅里叶级数分解,取其基波Iin对整个电路进行近似分析,有

结合式(2)~式(9),可以得到 Is和 PP 结构IPT 系统相应的输出电压Vo为

在实际的系统中,副边的输出电压还需要经过整流桥才能够输出成为直流电压。1998年Robertl Steigerwald提出实际PP结构整流桥接的负载可以等效为直接接在理想PP结构中的负载[6],即

结合上述式(2)~式(12)可得电压增益和效率。
3.3 NSGA-II算法配置PP结构IPT系统谐振网络参数
3.3.1 PP结构IPT系统模型整理
对上述模型进行整理,可以得到目标函数、约束条件以及优化变量及其范围。
(1)目标函数为

(2)约束条件为

式中:g1和g2分别为原、副边的品质因子相关的不等式约束;Qp和Qs分别为IPT系统的原边和副边的品质因子,品质因子太小会让谐振变差,太大会让系统变得敏感,鲁棒性变差,因此取值在1~10之间比较合适;g3为输入电流相关的不等式约束,需根据实际系统所使用的输入电源选择,因电源能力限制,可提供的电流不超过6 A。
(3)优化变量为

PP结构IPT系统本身具有5个谐振网络参数,其中,Cp和Cs可使用Lp、Ls和其他的参数代替,即
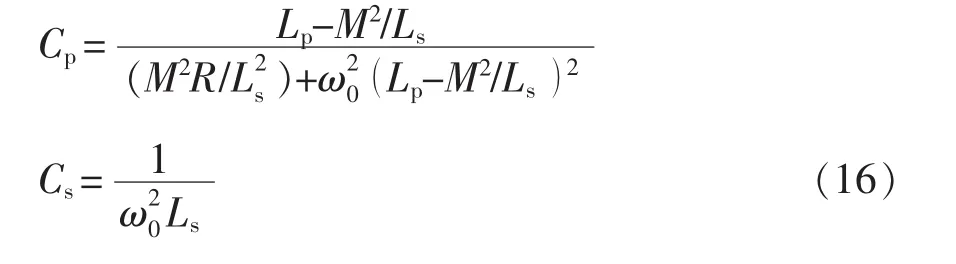
3.3.2 NSGA-II参数配置结果
使用NSGA-II多目标优化算法对模型进行优化,参数配置结果如图3所示。
图3中目标函数1的绝对值代表电压增益,目标函数2的绝对值代表系统功率传输效率。由图中可以看出,算法得到的帕略特解分布较好,2个目标的范围也很合适。但仅图3并不能说明NSGA-II得到的参数是合格的参数,为了检验参数是否合格,还需要通过仿真和实验验证谐振网络参数的有效性和准确性[7-8]。有效性是指采用优化后的谐振网络参数系统的完全谐振程度;准确性是指该模型、仿真以及实验中系统性能指标的吻合程度。
本文从上述帕略特最优解集中选取了3组解进行仿真和实验验证谐振网络参数的有效性和准确性。选取的最优解与对应的参数如表1所示。

图3 参数配置结果Fig.3 Parameter design results

表1 选取的最优解与对应的理想参数Tab.1 Optimal solution and the corresponding ideal parameters
3.4 谐振网络参谐振网络参数验证
3.4.1 理想参数的仿真验证
使用Matlab/Simulink工具箱,在搭建的PP结构IPT系统仿真文件上进行了仿真,理论参数仿真结果如表2所示。
对比表1和表2可以看出,仿真中采用了以上3种谐振网络参数的PP结构IPT系统的电压增益和传输效率和模型中的差距很小。这说明利用NSGA-II算法寻找IPT系统的谐振网络参数的准确率高。需要指出的是,仿真和模型的微小差距源自于阻抗模型本身只是一个近似等效模型,模型只选用了谐振电压电流的基波进行分析,并没有考虑对系统电压增益和效率影响很小的谐波成分。

表2 理论参数仿真结果Tab.2 Simulation results of theoretical parameter
3.4.2 实际参数的仿真验证
如第3.3节所述,实际系统的参数不可能和理想参数完全一样,只能够尽量接近。因此,本文根据理想参数选取了实际参数,如表3所示。
实际参数系统的仿真和数学模型分析结果如表4所示。

表3 根据理论参数选取的实际参数Tab.3 Actual parameters selected according to theoretical parameters
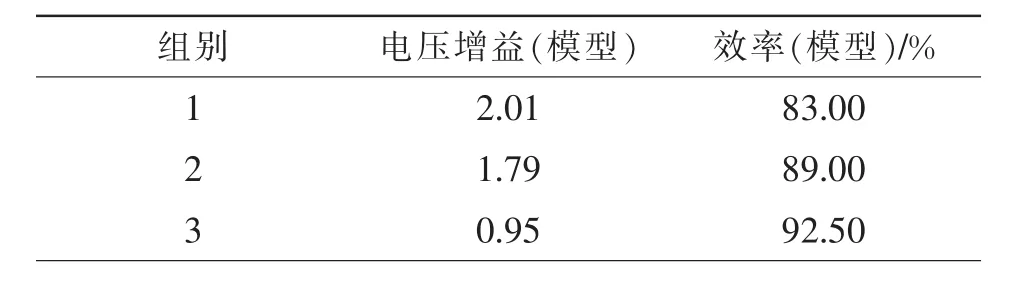
表4 实际参数仿真结果Tab.4 Simulation results of actual parameters
对比表3和表5的数据,表明实际参数下仿真和模型的电压增益相差不大,然而由于模型中忽略了谐波分量的影响,所以模型的结果优于仿真的结果。对比实际参数下仿真和模型的结果表明PP结构IPT系统的传输效率差距有点大,主要原因有以下两点:①建立的交流阻抗模型中忽略了谐波分量;② 在模型参数中,为了计算的简便,将所有电感自身的电阻均设置为0.1 Ω,而实际中,电感自身电阻与线圈的绕线方法和匝数等参数有关。表2和表4中的数据表明,实际参数中的电感电阻比理想参数中的电感电阻小,电感电阻上面损耗的能量也比模型中的小,所以实际参数的PP结构IPT仿真系统的能量传输效率比理想参数下的高。
第1组参数中Cp电压仿真波形如图4所示。由图4可见,仿真中系统的原边补偿电容的电压谐振波形很好,谐振效果满足系统要求。
3.4.3 实际参数的实验验证
为了验证配置参数在实际PP结构IPT系统上的有效性和准确性,搭建实验系统如图5所示。
采用实际谐振网络参数的PP结构IPT实验系统得到的电压增益和传输效率结果如表5所示。
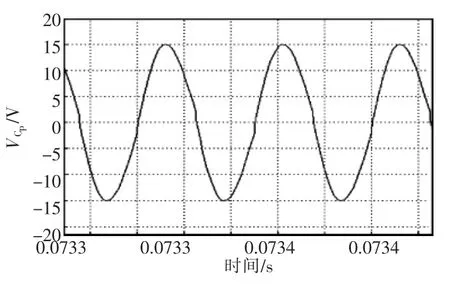
图4 第1组参数中Cp电压仿真波形Fig.4 Voltage simulation waveform of the Cpof the first set of parameters

图5 PP结构的IPT系统Fig.5 IPT system with PP topology
图6 为第1组参数的实验波形,图中原边补偿电容上的谐振电压波形表明系统的谐振比较理想(在未加软开关的前提下)。同时,对比表5和表4发现,实验结果和仿真结果相差很小,两者基本上是相符合的,这说明使用NSGA-II算法找到的理想参数来设计实际参数的准确性也很高。根据现场实验结果分析,造成两者结果差距的原因有:① 实验环境中存在着电磁干扰、测量误差等因素;② 实验中系统没有加入软开关电路,整个系统工作在硬开关状态下。

表5 实际参数实验结果Tab.5 Experimental results of actual parameters

图6 第1组实际参数的实验波形Fig.6 Experimental voltage waveforms of the Cpof the first set of parameters
4 结语
传统IPT系统的谐振网络参数配置方法可靠性不高,有着繁琐、低效且难以对多目标IPT系统进行参数配置等缺点。通过对IPT系统的参数配置的全面分析,本文将NSGA-II算法应用于谐振网络参数配置之中,利用遗传算法强大的优化性能,对谐振网络参数进行了配置,使得谐振网络参数的配置变得高效、简洁,并且可以对多目标IPT系统进行谐振网络参数配置。通过使用NSGA-II算法对预期目标为高电压增益和高效率的PP结构IPT系统进行谐振网络参数配置、仿真和实验验证,NSGA-II算法配置参数高效、简单且准确性高。
[1]赵争鸣,张艺明,陈凯楠.磁耦合谐振式无线电能传输技术新进展[J].中国电机工程学报, 2013, 33(3):1-13.
Zhao Zhengming,Zhang Yiming,Chen Kainan.New progress of magnetically-coupled resonant wireless power transfer technology[J].Proceedings of the CSEE,2013,33(3):1-13(in Chinese).
[2]Deb K,Agrawal R B.Simulated binary crossover for continuous search space[J].Complex Syst, 1994,9(3):115-148.
[3]尹洪,刘天琪,李樊,等.基于免疫遗传算法的含分布式电源配电网重构[J].电力系统及其自动化学报,2014,26(4):15-19.
Yin Hong,Liu Tianqi,Li Fan,el al.Distribution network reconfiguration with different distributed generation based on immune genetic algrithm[J].Proceedings of the CSU-EPSA,2014,26(4):15-19(in Chinese).
[4]Hu A P.Selected resonant converters for IPT power supplies[J].Researchspace, 2001.
[5]Steigerwald R L.A comparison of half-bridge resonant converter topologies[J].IEEE Transactions on Power Electronics,1988,2:174-182.
[6]马皓,周雯琪.电流型松散耦合电能传输系统的建模分析[J].电工技术学报, 2005, 20(10):66-71.
Ma Hao,Zhou Wenqi.Modeling analysis of inductively coupled power transfer systems based on current source resonant converter[J].Transactions of China Electrotechnical Society,2005,20(10):66-71(in Chinese).
[7]孙跃,王智慧,苏玉刚,等.电流型CPT系统传输功率调节方法[J].重庆大学学报, 2009, 32(12):1386-1391.
Sun Yue,Wang Zhihui,Su Yugang,et al.Power transfer regulation mode for current fed CPT system[J].Journal of Chong qing University,2009,32(12):1386-1391(in Chinese).
[8]王国东,乔振朋,王允建,等.磁耦合谐振式无线电能传输系统中线圈谐振特性研究[J].电源学报,2015,13(2):58-63.
Wang Guodong,Qiao Zhenpeng,Wang Yunjian,el al.Coil resonance characteristics of magnetically-coupled resonant wireless power transmission system[J].Journal of Power Supply,2015,13(2):58-63(in Chinese).
Parameters Design for IPT System Based on NSGA-II Multiobjective Optimization Algorithm
HUANG Yongcan,DAI Xin,ZOU Yang
(College of Automation,Chongqing University,Chongqing 400044,China)
The mathematical model of inductive power transfer(IPT) system is complex.The traditional harmonic parameter configuration method is inefficiency,inaccurate and difficult to configure parameters for multi-objective design.This paper proposes an efficient parameters configuration method using NSGA-II multi-objective optimization algorithm.After once run,NSGA-II can get many parameters,which can satisfy the requirement of system design.Taking the current-fed IPT system for example,we use NSGA-II to design parameters for the system.Simulation and experiment results show that configuration parameters obtained from this optimization algorithm can satisfy the expected goals of system design.
NSGA-II;current-fed IPT system;genetic algorithm;parameter configuration

黄永灿
黄永灿(1992-),男,通信作者,硕士研究生,研究方向:无线电力传输,E-mail:641656488@qq.com。
10.13234/j.issn.2095-2805.2017.4.65
TM732
A
2015-12-10
国家自然科学基金资助项目(51377183,51277192);重庆市国际科技合作基地资助项目(CSTC2015GJHZ40001)
ProjectSupportedbyNationalNaturalScienceFoundationofChina(51377183,51277192);Chongqing International Science and TechnologyCooperationBaseProject(CSTC2015GJHZ40001)
戴欣(1978-),男,博士,教授,研究方向:无线电力传输,E-mail:toybear@vip.sina.com。
邹洋(1989-),男,博士研究生,研究方向:无线电力传输,E-mail:525172210@qq.com。

