解决数学抽象性的几种思维策略

福建省三明市沙县金沙高级中学 黄含笑

解决数学抽象性的几种思维策略

福建省三明市沙县金沙高级中学 黄含笑

高中数学学习相比初中数学学习，思维层次提高了不少。如何通过思维引导，帮助学生摆脱抽象思维的困扰，尽快适应高中数学学习呢？笔者认为，提升学生的思维能力，加强思维方法引导，帮助他们掌握一些特殊的思维策略是一条有效途径。本文对于帮助学生摆脱数学抽象思维困扰有一定的指导意义。

系统化；具体化；几何化；极限化；多样化

带着对高中学习的期待，伴着对高中生活的向往，初中的优秀学子们进入了高中数学课堂。随着学习的深入，他们都感觉到了“理想很丰满，现实很骨感”，相当多的同学出现了严重的学习障碍，甚至谈数色变，影响了他们学习的积极性。为了帮助学生摆脱抽象思维的困扰，可以从如下几个方面开展数学教学工作。

一、零散知识系统化

很多时候，大家往往都认为是学习内容多导致学生的学习困难。这是一个误解，困扰学生的不是学习内容多，而是学习内容杂乱，没有形成知识系统。单独的知识点学习，学生只见树木不见森林，因而学习的意义不够明显；系统化的学习通过把知识融会贯通，既见树木也见森林，实现的不仅仅是简单的知识积累，而且是一个数学能力的飞跃过程。学习的意义一下子得到彰显，学生学习的动力也更加充足。

在函数学习中周期性与对称性是学习的一个重点，但学生往往容易搞混淆，这时我们就要进行系统化的归纳，让学生做学习笔记如下：

1.函数周期性的常见形式

2.函数的周期性与对称性辨析

一般的，我们有奇函数关于原点中心对称；偶函数关于y轴轴对称。函数关于点的中心对称，我们可以借助正弦函数来帮助理解，它的对称中心是；函数关于直线轴对称，我们也可以借助正弦函数来帮助理解，它的对称轴为从正弦函数看，周期性和对称性虽然不相同，但有一定的联系。

函数的周期性与对称性在表达式方面，学生很容易混淆，我们可以从下面的整理中帮助学生辨析清楚：

为了区分函数的周期性与对称性，可以用口诀归纳为： 同号是周期， 异号变对称。

3.周期性与对称性之间的关系

利用函数周期性对称性解题的例子比较多，这里举一个例子。

当然，系统化整理好的笔记也是开放性的，要随着学习与认识的深入进一步补充完善。学生通过对比、推理、总结等一系列思考过程，就能够真正掌握这些知识要点。

二、抽象表达具体化

高中同学感到数学难学，主要是数学的抽象性太强，克服抽象性的对应办法就是具体化。具体化在选择填空题中常常表现为取特殊值。我们看下面一个例子。

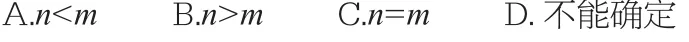
由于这是一道选择题，因此，我们也可以通过特殊值代入进行具体化处理。如，我们令则；再令，则有解得这与题中的矛盾，故排除C答案。再令则有：

如果不进行具体化的特殊值处理，很多学生就不知道从哪里入手解决问题。当然，在特殊值具体化的基础上，还要慢慢引导学生抽象化地书写解题过程。当学生真正理解了抽象性的表达，就能够在具体与抽象之间自由地展开思维的翅膀。

在具体化的运用中，有个很典型的运用，就是抽象函数具体化。四种抽象函数：它们具体化后对应为一次函数、指数函数、对数函数、幂函数。这样具体化后可以很容易地画出抽象函数的草图，对于解决抽象函数问题具有很大的帮助。

三、代数问题几何化

数形结合是学好数学的基础。如例1，通过对称性使问题变得直观可解。一般地，数轴、平面直角坐标系、集合中的韦恩图、向量、对称性、周期性，这些都是我们数学形象化的有效工具。

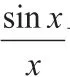
数形结合得以实现，往往是要赋予代数表达一个几何的意义，如距离、斜率、面积等。

四、复杂对象极限化

有个数学游戏是这样的：两个人轮流往圆桌上放一元的硬币，谁最后一个放上去恰好铺满圆桌，谁就算赢。如果你来参与游戏，你选择先放还是选择后放？极端化的思考是硬币和圆桌一样大小，先放的放上去，后放的没有地方放，所以先放的赢！但桌子比硬币大很多呀？这时，我们先放的可以放最中央，然后根据圆的对称性，不论后放的放哪里，先放的都可以在对称位置放，确保最后恰好铺满圆桌。

解数学问题时，我们经常要面对的是一个复杂的变化过程，这时我们往往需要了解其变化的趋势，根据变化趋势的极限值来判断结果。如趋近于0的正数，其倒数就趋近于正无穷大，而趋近于0的负数，其倒数则趋近于负无穷大等等。

因为这是一个奇函数，所以首先可以排除选项A。接下来就需要有极限的思维了。当时，由于是有界的，分母趋近于无穷大，故函数值趋近于0，所以排除C。为了筛选B、D中的正确选项，我们取有从而排除了B，最后选出正确选项D。这里虽然是用了不太严格的极限化推理，但从变化趋势看，是没有问题的。

我们再来看一道例题。

极限化的思考对于填空、选择等小题很有效。思考干脆利落，思路敏捷，节省了大量的解题时间，因此，我们要学会很好地利用这一思考工具。对于数学大题，我们很多时候也可以通过极限情况寻找到解题的最终结果，并启发解题思路。

五、思考角度多样化

解数学题时若能换个角度思考，常常会有一些新的发现，或者有一些巧妙的解法。很多同学看到选择题都是先分析题干，再看选项。如果我们先分析选项，再回头看题干，很多时候节约的不仅仅是阅读题目的时间，还可以找到快捷的解法。

这是分段函数与不等式结合的选择题。如果直接解不等式，就需要同时考虑定义域这一前提，而且容易出错。如果我们从选项来思考，发现A、C选项的差别只是有没有包含0，令代入符合题意，因此，是需要取值的。排除了不包含0的C、D。再令由也是符合题意的。因此排除B，选A。

所以解选择题这种客观题的时候，我们可以改变一下常规思路，不着急从题干到选项，而是直接先分析选项，这样常常会有快捷的解答方法。

解数学问题时还有一种逆向思维，即从结果出发寻找原因，这也是换个角度思考，这在数学分析法解题中有大量的运用，这里不再赘述。

高中数学思维能力提升的途径很多，本文无意追求面面俱到的论述，只是选取摆脱数学抽象化困扰中比较典型的几个方面展开论述，提出一些应对思维抽象性的解决策略，以起到抛砖引玉的作用。

[1]徐月秀.浅谈数学思维策略在解题中的运用[J].数理化学习，2016（01）：41-42.

[2]杜学文.浅谈高中数学解题的思维策略[J].理科考试研究，2014（06）：32.

[3]卢浩慧.高中数学解题思维策略研究[D].河南师范大学，2015（04）：01.