“解决问题的策略”教学设计
赵云峰
[摘 要]转化是指把一个数学问题变为一类已经解决或比较容易解决的问题,从而使原问题得以解决的一种策略。在教学中,先由两幅图引入新课,让学生在尝试解题的过程中自觉运用转化策略,在掌握了转化策略后回忆以往用转化策略解决过的问题,在解决新问题的过程中完善对转化策略的认知,从而获得成功的体验。
[关键词]转化;解决问题的策略;回忆;体验
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)20-0059-02
【教学内容】苏教版数学五年级下册“解决问题的策略”第105~106页的例1、“练一练”和练习十六的第1~3题。
【教学目标】
1.让学生初步学会运用转化的策略分析问题,确定解决问题的思路,并能根据问题的特点确定具体的转化方法,从而有效地解决问题。
2.在具体的问题情境中,让学生体会运用转化策略解决问题的价值,感受转化策略是解决问题的常用策略。
【教学重点】初步学会运用转化策略分析问题、解决问题。
【教学过程】
一、情境呈现,在矛盾冲突中自然引入新课
师:图1中有两个图形,仔细观察后想一想这两个图形的面积有怎样的关系。
生1:两个图形的面积一样大。
师:你有什么理由来说明这两个图形的面积是一样大的?
生1:用数方格的方法来比较。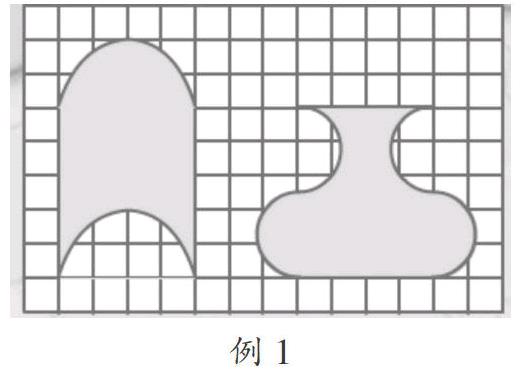
师:这确实是一种方法。我们在数方格时,可以先把图中的方格线补画完整。有不同的想法吗?
生2:可以将这两个图形都转化成长方形,再比较它们的大小。
师:非常好!这两幅都是不规则图形,不便于直接比较,我们可以运用转化的方法将这两个图形转化成我们已经学过的图形。今天我们一起学习“用转化的策略解决问题”。
【设计意图:对于例1的两个不规则图形,要转化成已经学过的图形,学生会感到比较难。因此,教师没有兜圈子,而是通过让学生独立思考问题“这两幅图形的面积有怎样的关系?”,打破学生的认知平衡,当强烈的求知欲望驱使学生去寻找方法时,教师再及时引入新课,水到渠成。】
二、自主探索,在尝试解题中运用转化策略
师:现在我们就用转化的策略将这两个图形转化成长方形。先在方格纸上画一画,完成后再在小组里说一说自己是怎样思考的。
师:现在谁愿意说一说你是怎样转化的?
(在学生回答问题时,教师要引导学生说出是怎样将这两个图形转化成长方形的。对于第一个图形,是怎样把上面的半圆进行平移的,上面的半圆向什么方向平移了几格;对于第二个图形,是怎样把左右两个半圆进行旋转的,左右两个半圆分别按什么方向旋转了多少度。)
师:现在能看出这两个图形的面积有怎样的关系吗?
【设计意图:在呈现例1后,学生已有了“将这两个图形分别转化成长方形,再比较它们的大小”的策略,所以让学生独立“转化”已成为可能。因此,教师只需要通过多个追问,就能让学生明白转化方法的同时感悟到“将两个不规则图形转化成学习过的长方形后,再比较它们面积的大小”是一个简单有效的解决问题的方法。】
三、合作思考,在回忆交流中体会转化价值
师:现在请大家以小组为单位,思考曾经运用转化的策略解决过哪些实际问题,并把这些问题写下来。
(学生小组讨论)
师:现在请说一说我们曾经运用转化的策略解决过哪些实际问题。
生1:在推导三角形面积公式时,将两个完全一样的三角形转化成平行四边形。
师:现在我们一起回忆三角形面积公式的推导过程,看看是怎样运用转化的策略推导出三角形面积公式的。
(教师用两个完全一样的三角形演示推导过程,同时请学生完成填空题:两个一样的三角形拼成了一个 ,拼成的 的底等于 ,高等于 ,因为平行四边形的面积= ,所以三角形的面积= 。)
师:将没有学习过的知识转化成已经学习过的平行四边形面积计算,就能得出三角形的面积计算方法。
【设计意图:用转化的策略推导几何形体中的面积计算公式,是学生已经具有的“转化”经验,所以当学生说出三角形的面积公式推导过程之后,教师有意将主要推导过程呈现出来,帮助学生进一步感悟转化的思想。】
师:你还能想到在哪里也运用了转化的策略?
生2:计算异分母分数相加、减时,將异分母分数转化成同分母分数。
生3:计算小数乘法时,先将小数乘法转化成整数乘法再计算。
师:这些都有什么共同点?
生4:都是把新的问题转化成熟悉的或已经解决过的问题。
师:转化是一种常用的,也是非常重要的解决问题的策略。在我们以往的学习中,早就运用这一策略分析并解决问题了。因此,在比较两个图形面积的大小时,将不规则的图形转化成已学过的图形后再思考,显得更加方便。在以后的学习中,如果遇到一个陌生的问题时,你们也可以运用转化的策略来试一试。
【设计意图:在之前的学习中,已经有许多新知识都是由学生自己通过转化的策略获取的,但是由于不作为一个整体进行教学,学生对“转化”的认识并不深刻。为此,教师在教学时引领学生回忆从几何形体知识中面积公式的推导,到异分母分数加减、小数乘法计算的转化,让学生体会转化无处不在,从而感悟转化在解决问题中的作用。】
四、自主运用,在解决问题中认识多种转化
习题1:课本的“练一练”。
师(引导学生观察图形,让学生理解题意后尝试解答):你们是怎样转化问题的?转化时,图形的什么在变,什么没有变?通过解决这个问题,你对转化策略又有了什么认识?运用转化策略时要注意什么?
习题2:两个小队的少先队员去植树,一共植了34棵。其中第二小队比第一小队多植4棵。两个小队各植树多少棵?
师:老师将这道题转化成下面的线段图,你能很快列出式子吗?
师:通过将实际问题转化成线段图,就可以很快找出数量之间的关系,从而解决问题。因此,在解题遇到困难或感觉题目太复杂时,我们应该要想到转化的策略。
【设计意图:这是教师有意设计的补充题。借助线段图解决问题,是学生经常用到的方法,因为从线段图中可以很快找出数量关系,从而解决问题。其实,将实际问题用线段图表示,也是一种转化策略,教师要有意让学生从多方面感受“转化”,引领学生在以后的学习活动中灵活选用转化策略解决问题。】
习题3:练习十六第1题。
师:怎样计算右边图形的周长比较简便?
(在学生回答的过程时,教师动态演示把右边图形转化成长方形的过程)
师:如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
师:解决这个问题的策略是什么?
五、拓展延伸,在变式练习中强化转化策略
习题4:练习十六第2题。
(让学生解决问题后说说思考的过程。对于最后一个图形,可以引导学生先从空白部分的面积是整个图形面積的几分之几进行思考,再想涂色部分的面积是整个图形面积的几分之几。)
【设计意图:本节课的练习除了教师补充的一道题,其余全是教材中的题目,教师只需引领学生掌握教材中练习题的解题思路。对于练习十六第2题中的最后一个图形,如果只是将涂色部分通过转化拼成10个小正方形,很多学生还是很难理解,如果引导学生逆向思考,从“空白部分的面积是整个图形面积的几分之几”入手,更利于学生快速解决问题。】
六、回顾反思,在回味解题中提升思维品质
师:回忆我们今天运用转化的策略解决过的问题,你对转化的策略又有了哪些新的认识?
(引导学生多方面回忆转化策略在解决问题中的运用)
(责编 金 铃)

