基于RomaxCLOUD的对数素线圆柱滚子凸度量的有限元分析
牛振华,邱明,杜辉,庞晓旭,牛青波
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳轴承研究所有限公司,河南 洛阳 471039)
轴承滚子没有修形(直素线)的情况下,产生边缘应力集中效应,滚子端部会出现过早疲劳及磨损甚至破坏[1]。研究表明,轴承寿命约与应力的7次方成反比[2],滚子端部应力的急剧增加会降低轴承寿命,故有必要对滚子进行修形,对数曲线修形是最为理想的修形方式[3],在一定载荷范围内,合理的凸度量和对应的凸度方程可改善滚子边缘效应。直素线滚子的轴承进行设计时必须根据实际运行工况对滚子素线进行对数修形,从而确定合理的凸度量和对应的凸度方程。
要得到合理的凸度量与对应的凸度方程,需对滚子轴承进行应力分析,传统的弹性力学和Hertz接触理论无法对滚子修形后的应力进行分析。鉴于此,基于RomaxCLOUD对某轴系两端圆柱滚子轴承进行应力分析,并确定对数修形滚子的最优凸度量。
1 轴系模型
1.1 圆柱滚子轴承结构参数
以某轴系两端的圆柱滚子轴承为例进行分析,套圈及滚子材料为GCr15,其主要参数见表1。

表1 NU2215轴承主要参数Tab.1 Main structural parameters of bearing NU2215
1.2 轴系模型的建立
以RomaxCLOUD为平台建立轴系模型,如图1所示,在轴的中点施加径向载荷Fr,左端的试验轴承内圈采用右端轴肩定位,右端的试验轴承内圈采用左端轴肩定位,约束两轴承外圈的6个自由度。轴承内圈旋转,转速为1000 r/min,径向游隙为10μm,轴承无预紧力,该轴系初始温度设置为20℃,轴承内圈与轴采用过盈配合。

图1 轴系模型Fig.1 Axis model
2 凸度设计
滚子对数素线方程为[4-6]
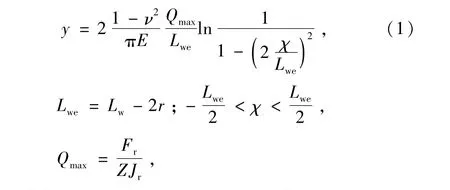
式中:Qmax为滚子承受的最大载荷;Lwe为滚子有效长度;对于滚子轴承,取4.08。
凸度近似值为
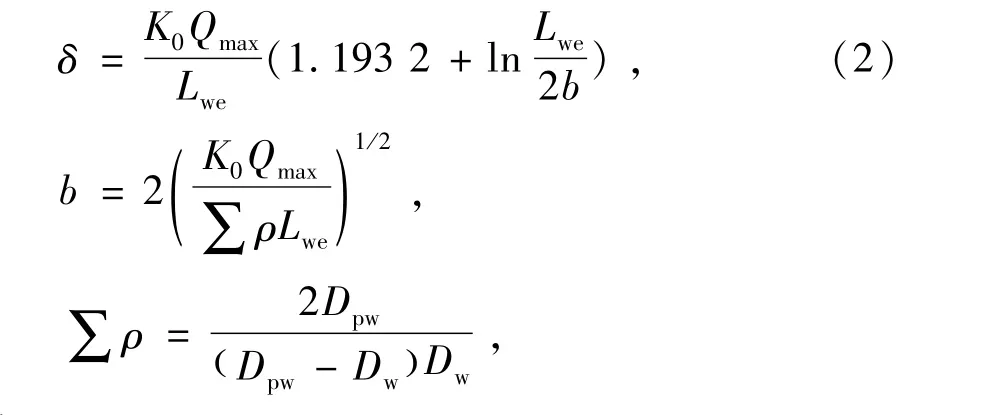
式中:K0为材料常数,对于普通轴承钢,K0=2.81×10-6mm2/N;b为滚子与滚道接触区半宽;∑ρ为滚子与滚道的综合曲率。
滚子的最佳凸度与轴承所受载荷有关,以轴承径向载荷作为设计载荷,轴承在径向载荷Fr=0.1Cr~1.0Cr作用下,由(1)式得到对应的对数方程,由(2)式得到不同径向载荷下滚子对应的凸度量(表2)。

表2 不同径向载荷下的滚子凸度量Tab.2 Crowning values of roller under different radial loads
3 有限元分析
3.1 直素线滚子轴承接触应力分析
根据实际工况,轴承承受径向载荷约为0.35Cr[7],因此在轴系中部施加径向力90 kN,由于径向力加载于轴的中点不是直接加载于轴承上,两端轴承除受45 kN的径向载荷外还受到一定弯矩作用,弯矩大小为22500 N·m。由于两端轴承受力对称,仅对左端轴承进行有限元分析,以图1左端直素线滚子轴承左视图轴承中心为极坐标原点,滚子与内外滚道最大接触应力为极轴,极轴对应于角度为0的方向,轴承逆时针方向标定位置角,绘制极坐标图如图2所示,其中轴承径向加载方向最下方处滚子位置角为90.003°,从图中可以看出,仅有7个滚子受载,内圈最大接触应力始终比外圈最大接触应力大,处于90.003°位置处的滚子受载最大,与90.003°位置角两边对称的滚子所受最大接触应力值相差不大,最大接触应力呈对称分布。
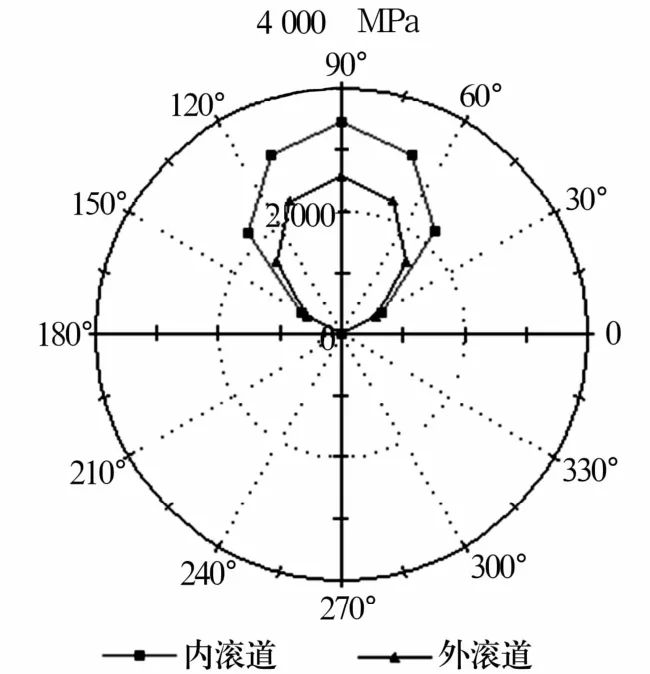
图2 滚道周向最大接触应力分布图Fig.2 Maximum stress distribution diagram in circumferential direction of raceway
不同位置角处直素线滚子与滚道的接触应力沿滚子素线方向上的变化曲线如图3所示,从图中可以看出:1)90.003°位置角两边的对称滚子应力值相差不大,应力对称分布,应力曲线大致重合;2)直素线滚子轴承内外圈均出现边缘应力集中及偏载现象,滚子与内圈两端接触应力差值大于滚子与外圈两端接触应力差值,内圈比外圈偏载现象严重,90.003°位置处的滚子偏载现象最严重,与90.003°对称位置处的滚子偏载现象也呈对称分布,越靠近90.003°位置处的滚子偏载现象越严重。内圈最大接触应力为3428.91 MPa,外圈最大接触应力为2569.97 MPa。
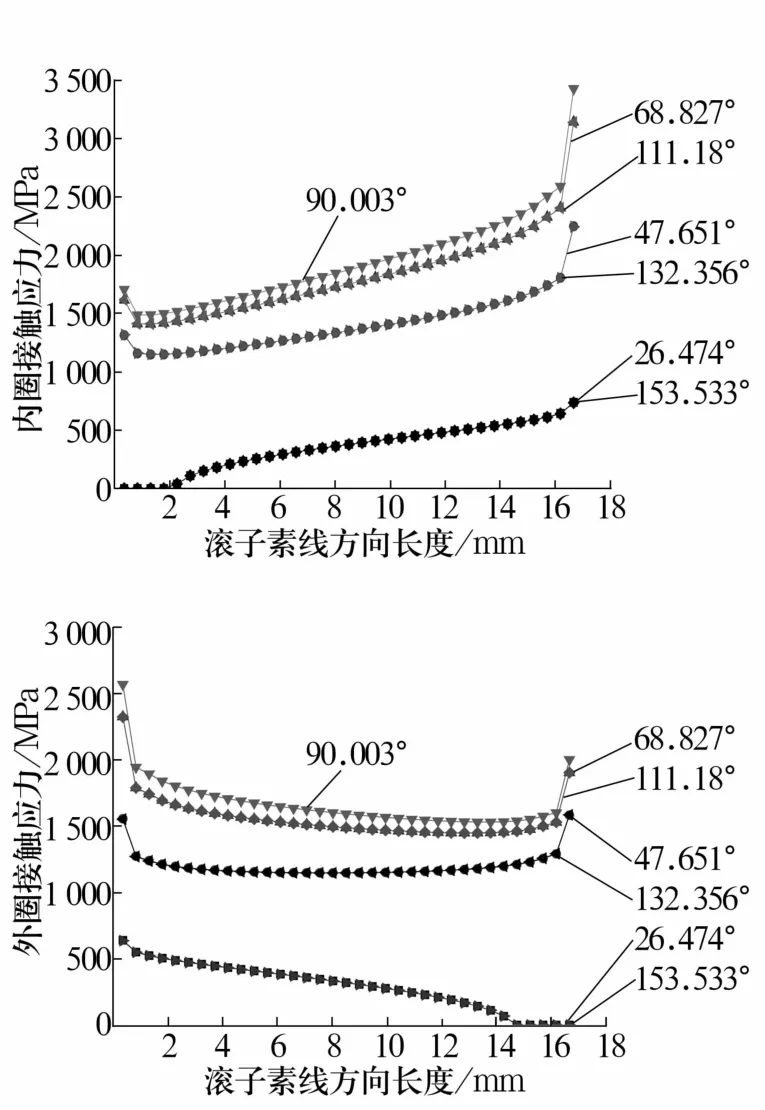
图3 直素线滚子与套圈的接触应力Fig.3 Contact stresses of straight generatrix rollers and rings
在滚子与滚道循环交变应力作用下,内圈最大接触应力比外圈最大接触应力大,内圈比外圈易出现疲劳失效,且滚子出现偏载时,会加速轴承的疲劳损坏[8]。为消除边缘应力集中现象,需对滚子进行对数修形。
3.2 对数修形滚子轴承接触应力分析
根据表2得到不同载荷下的滚子凸度量,轴承内外圈滚道最大接触应力值随凸度量的变化如图4所示。由图可知,在相同载荷作用下,内圈最大接触应力始终大于外圈,随凸度量增大,内外圈最大接触应力先减小后增大,凸度为6.936μm时,内外圈最大接触应力达到最小,当凸度大于6.936 μm时,内外圈接触应力又逐步增大。这说明轴承在径向载荷45 kN作用下,在所选的凸度范围内滚子凸度值6.936μm为最佳设计。
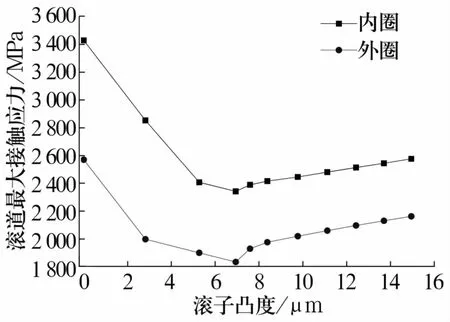
图4 接触应力随凸度量的变化Fig.4 Variation of contact stresses with crowning values
当凸度值为6.936μm时,不同位置角处对数修形的滚子与内外圈滚道的接触应力沿滚子素线方向上的变化曲线如图5所示,内圈接触应力最大值为2372.22 MPa,比直素线滚子与内圈的接触应力降低了44.54%;外圈接触应力最大值达到1879.77 MPa,比直素线滚子与外圈的接触应力降低了26.86%,修形之后轴承最大接触应力明显降低。

图5 对数修形滚子与套圈的接触应力Fig.5 Contact stresses of logarithmically profiled rollers and rings
凸度值为6.936μm时,在不同载荷作用下位置角为90.003°的滚子与内外圈接触应力如图6所示。由图可知,内外圈接触应力随滚子素线长度变化规律一致,当径向载荷低于0.5Cr时,滚子和滚道的有效接触长度较大,此时滚道所受应力比较均匀;当径向载荷大于0.5Cr时,滚子与滚道完全接触,滚子与内外滚道接触长度不再变化,但接触面积一直增大,滚子端部开始出现应力峰值,随着载荷继续增大,轴承偏载现象越严重,故轴承承受的径向载荷最好不超过0.5Cr。当轴承径向载荷为1.0Cr时,内滚道最大接触应力已达到5709.317 MPa,外滚道最大接触应力达到4157.455 MPa,均已达到疲劳极限。

图6 不同载荷下滚子与套圈接触应力曲线Fig.6 Contact stress curves of rollers and rings under different loads
4 结论
1)采用对数素线修形滚子的轴承可以有效地避免或降低边缘应力集中。
2)当轴系在径向载荷90 kN作用下,在加工条件允许的情况下应尽可能地使滚子凸度量接近6.936μm。
3)滚子与滚道的有效接触面积随载荷增加而增大,当轴承径向载荷小于0.5Cr时,滚子与滚道接触应力分布比较均匀;当径向载荷增加到0.5Cr后,滚子端部开始出现应力集中现象;当径向载荷大于0.5Cr,轴承偏载现象严重。故应保证轴承所受径向载荷在0.1Cr~0.5Cr范围内。

