高速双转子试验机主轴系统模态分析
马俊,司东宏,薛玉君,,董永祥
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.河南省机械设计及传动系统重点实验室,河南 洛阳 471003)
主轴系统的动态特性是直接影响高速双转子试验机整体性能的主要因素。主轴轴系受力复杂,不仅承受径向加载力,还承受转子旋转质量惯性力引起的周期性振动,而周期性振动会使轴系的疲劳寿命降低;因此,分析试验机主轴系统的动态特性对于提高试验机整体稳定性、可靠性和延长使用寿命具有重要的意义[1]。
文献[2]分别分析了双转子轴承试验机左右端主轴的固有频率,计算出单根轴的临界转速,由此得出单根轴的固有频率满足使用要求。然而,双转子轴承试验机单根轴的模态变化不能等同于双轴耦联时的模态变化,因此,使用有限元分析软件ANSYSWorkbench分析双轴耦联时的轴系模态变化,同时考虑高转速轴系旋转时产生的预应力对轴系模态的影响。
1 模态分析理论
模态分析是研究机械结构动力学特性、振动分析和动态优化设计的常用方法。多自由度结构系统的动力学方程可以表示为[3-4]
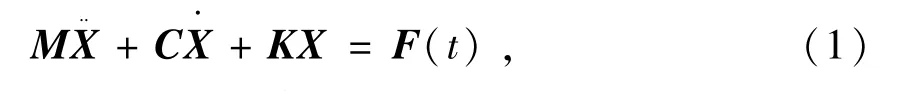
式中:M,C,K分别为结构系统的质量、阻尼、刚度矩阵;F(t)为外激励矢量;X为位移矢量。
在实际工况中,阻尼对结构的固有频率和振型影响不大,则无外载荷作用且忽略阻尼时,可将(1)式简化为

当轴系旋转时,由于离心力的作用会产生一定的旋转预应力,从而影响到轴系的模态振动性能。因此,在考虑预应力的情况下,(2)式方程解的形式可表示为
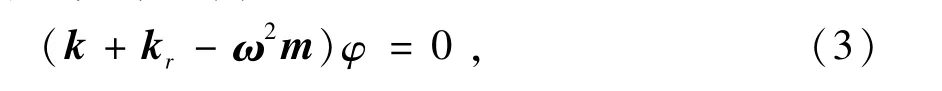
式中:kr为预应力刚度矩阵;m为振幅列阵;ω为角频率;φ为初相角。通过求解上式可以得到ω1,ω2,…,ωn等n个固有频率,并且满足0≤ω1<ω2<…<ωn。
2 主轴系统有限元分析
2.1 轴系模型的建立
使用Unigraphics软件建立试验机主轴系统结构模型,主轴系统主要有内轴、外轴、陪试轴承(角接触球轴承、圆柱滚子轴承)、试验轴承(角接触球轴承)、径向加载轴承等组成(图1)。试验轴承将内轴和外轴耦联在一起。陪试角接触球轴承分别装在内轴左端和外轴右端,陪试圆柱滚子轴承装在外轴左端,主要对轴系起支承作用;径向加载轴承对轴系不起支承作用,计算时可以忽略其刚度。为了提高网格划分质量并降低有限元分析时间,建模的过程中忽略一些不影响分析结果的倒角、倒圆角、孔等特征[5-7]。
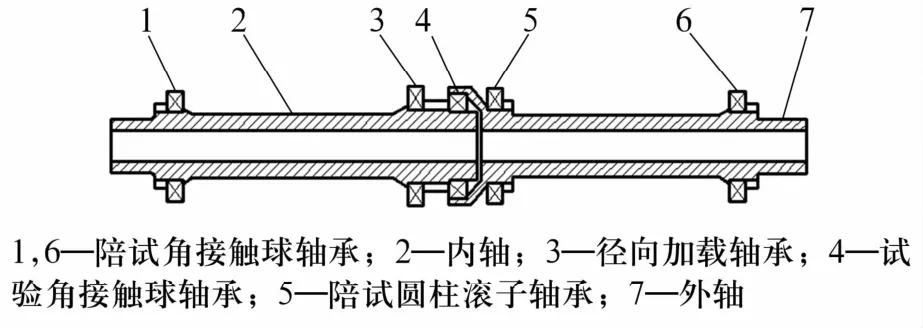
图1 轴系模型Fig.1 Shafting model
2.2 材料特性
主轴是轴承试验机的关键部件,必须具备足够的强度、刚度及耐磨性,且需要热处理变形小,因此需选择弹性模量、泊松比、屈服强度合适的材料。根据以上特点,主轴材料选用42CrMo,线性各向同性,详细参数见表1。

表1 主轴材料属性Tab.1 Material properties of spindle
2.3 有限元模型的建立
通过Unigraphics将轴系模型导成ANSYS Workbench分析软件可以识别的X_T格式。根据本次分析所用计算机的配置及对分析结果的精确度要求,选用了Sizing划分网格,网格单元类型为CTETRA(10),单元大小为15;部件中的单元总数为34179,节点总数为57438,有限元模型如图2所示。

图2 有限元模型Fig.2 Finite element model
2.4 轴承刚度的计算
根据试验机主轴系统装配方式可知,陪试轴承和试验轴承对主轴系统起支承作用,需要计算其支承刚度,一般将轴承简化成弹簧支承。实际工况中,轴承只有支承刚度而没有拉刚度,因此,圆柱滚子轴承只有一个方向的支承刚度,而角接触球轴承接触力比较复杂,在2个互相垂直的方向各自建立一个弹簧支承,轴承支承简化效果如图3所示。
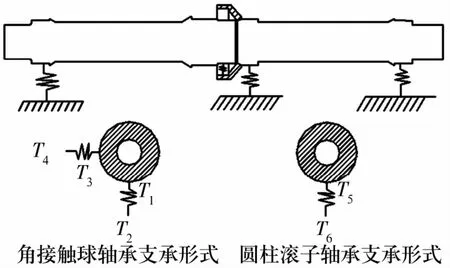
图3 轴系支承示意图Fig.3 Diagram of shafting support
现计算出满足设计要求的轴承刚度的最小值,支承轴承参数见表2,假设不考虑轴系上不同型号轴承的交叉刚度和阻尼的影响,只考虑轴承对轴系支承正刚度的作用[8-9]。
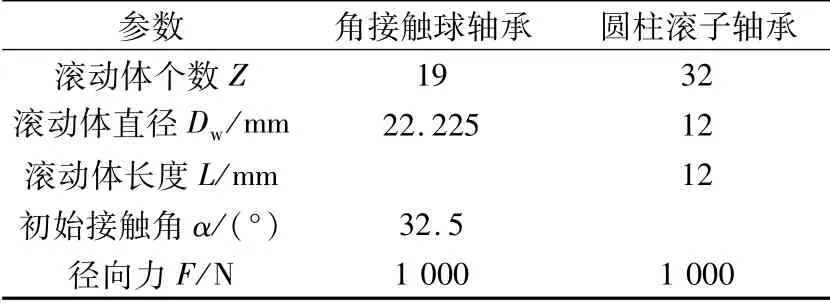
表2 轴承参数Tab.2 Parameters for bearing
根据经验公式[10]可知,角接触球轴承及圆柱滚子轴承的径向刚度分别为
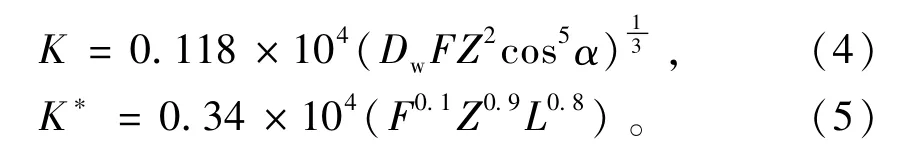
将表2中的参数代入(4),(5)式可得K=176957.4369 N/mm,K*=1120621.355 N/mm。
2.5 边界条件
在ANSYS Workbench中,约束角接触球轴承T2和T4的全部自由度,T1和T3的轴向移动自由度;约束圆柱滚子轴承T6的全部自由度,如图4所示。
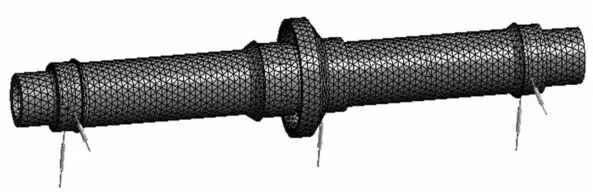
图4 边界条件Fig.4 Boundary condition
2.6 模态分析
双转子轴系设计通常只做静态下的模态分析,不考虑轴旋转时产生的预应力对轴系模态的影响,但在实际工况下,轴系旋转时产生的预应力不仅会影响轴系的刚度和强度,而且也影响轴承刚度;随着轴系转速的升高预应力会变大,从而改变与内外圈的接触角,使轴承的刚度软化,并对轴系的模态产生相应影响[11]。
考虑到轴系旋转形成的预应力对轴承刚度的影响,分析轴系在静态和不同转速下的预应力对轴系模态的影响,其趋势如图5所示。由图可知:静态下轴系模态的各阶固有频率值大于考虑预应力的各阶固有频率值,这是由于轴系旋转形成的预应力弱化了轴承的支承刚度,从而降低了固有频率;而随着转速的升高,轴系的固有频率下降越来越明显,当转速达到15000 r/min时,轴系1阶固有频率与静态下的1阶固有频率相比降低了25.9%,这是因为随着转速的增加,轴系产生的预应力增大,使球与内圈的接触角增大,与外圈的接触角减小,并改变了接触力的大小,使轴承的刚度随着预应力的增加而降低,最终轴系固有频率因轴承刚度的降低而减小。
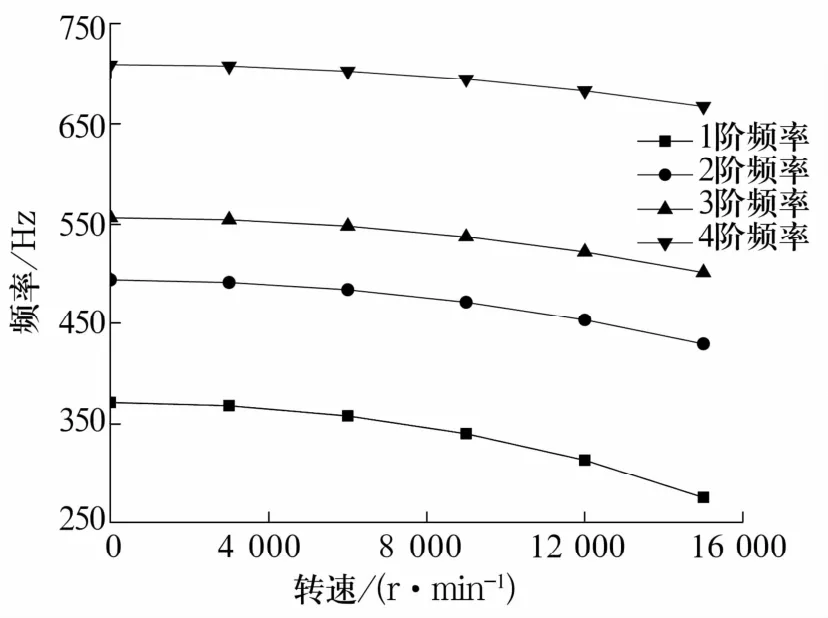
图5 不同转速下轴承各阶固有频率的变化趋势Tab.5 Variation trend of each natural frequency of bearing under different speeds
从图中还可以看出:1阶固有频率的变化最为明显,这说明预应力对1阶固有频率影响较大,为改善预应力对主轴模态频率的影响,轴系工作时,应增加与其对应的轴向力,提高轴承刚度。
3 轴系临界转速的计算
临界转速是轴系设计时工作转速避开共振频率点的主要参考依据,轴系在临界转速附近工作时,将产生剧烈的振动,长时间运行会造成主轴部件的严重弯曲变形,甚至会造成转子和轴承的破坏[12]。通过分析计算轴系的模态,求得各阶固有频率,从而确定轴系各阶临界转速。临界转速与固有频率的关系为[13]

式中:n为临界转速,r/min;f为固有频率,Hz。
3.1 Campbell 图求解
在ANSYS Workbench中,通过不同转速下的多载荷步模态分析,可以获得Campbell图并能得到轴系的临界转速,轴系的Campbell图如图6所示。实际工况中轴系的工作转速小于1阶临界转速,因此只关注1阶临界转速值,约为23206.2 r/min。
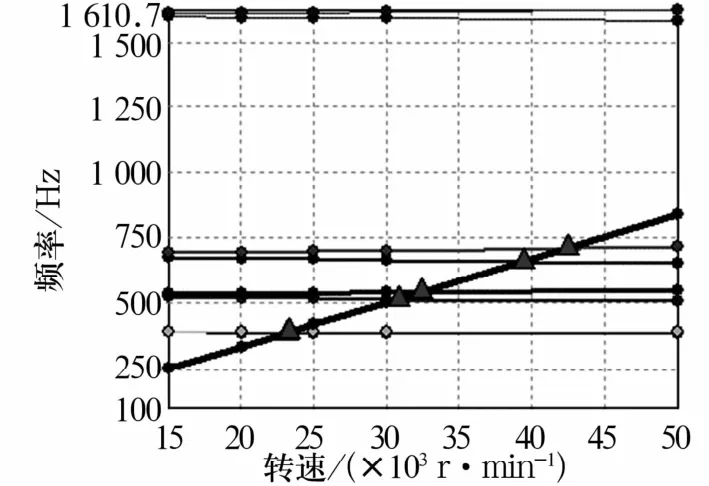
图6 Campbell图Tab.6 Campbell diagram
3.2 理论计算值
轴系由内轴和外轴通过试验圆柱滚子轴承连接在一起,因轴的刚度较大,故忽略轴的弹性而将其设为质量块,轴系上的轴承简化为弹簧,所以整个轴系的简化模型如图7所示。
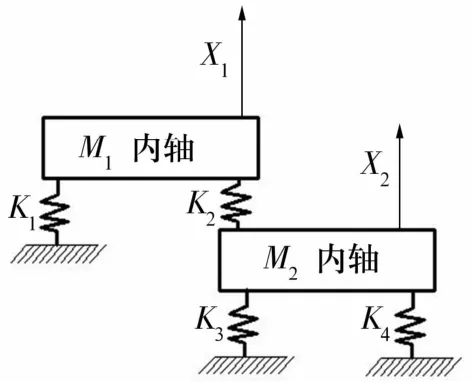
图7 轴系简化模型Tab.7 Simplified model for shafting
轴系简化模型中:X1,X2分别为内、外轴的位移;M1和M2分别为内、外轴的质量,M1=50.53 kg,M2=42.72 kg;K1~K4为轴承的刚度,由(4),(5)式求得K1=K2=K4=K=176957.44 N/mm,K3=K*=1120621.36 N/mm。
由轴系的简化模型图建立能量方程式,系统在任意时刻的动能T和势能V分别为
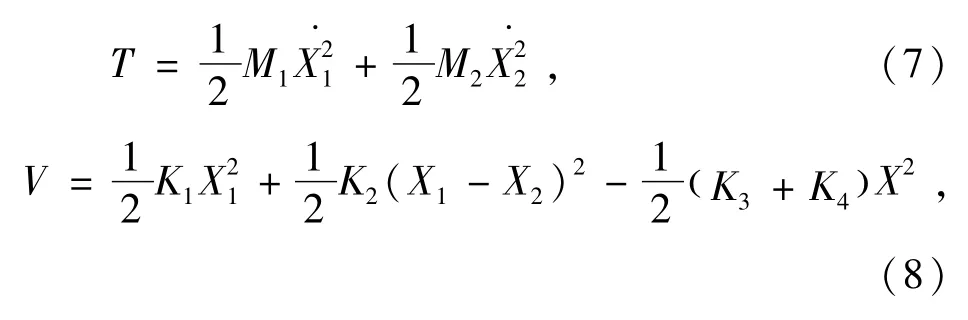
由(7)式减(8)式可得Lagrange函数为
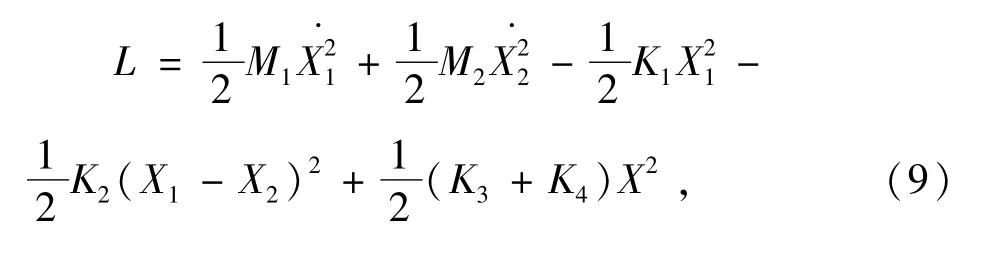
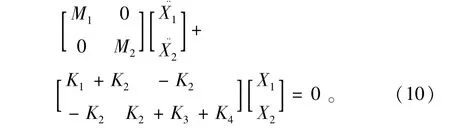
对比理论计算与有限元分析的结果可知:理论分析值略大于有限元分析值,这是由于有限元软件自动考虑了主轴材料的阻尼。根据轴设计手册可知,为了轴系的安全运行,通常取轴系1阶临界转速值的70%作为轴系在刚性阶段的极限工作转速。使用2种方法得到的1阶临界转速分别为23206.2 和 24660 r/min,其 70% 分 别 为16244.34和17262 r/min,均高于主轴系统最高设计工作转速15000 r/min,说明试验机轴系的设计符合要求。
4 结束语
通过ANSYSWorkbench中Block Lanczos有限元法计算了轴系静态下和预应力下的2种模态频率值,对比可知:轴系转速在3000~15000 r/min时,预应力下的模态值都低于静态下的模态值,且随着转速的升高差值越来越大;当转速达15000 r/min时,1阶固有频率相差了25.9%,表明预应力对轴系的影响明显,因此模态分析时应考虑预应力的影响。
根据Campbell图和理论分析法获得轴系的1阶临界转速分别为23206.2和24660 r/min,均远大于主轴的设计工作转速,可以满足设计要求;而有限元分析的数值小于理论值,说明有限元分析的数值比较保守,在实际工况中,为了安全考虑采用此临界转速值。

