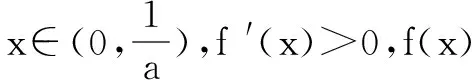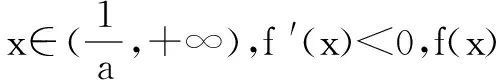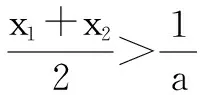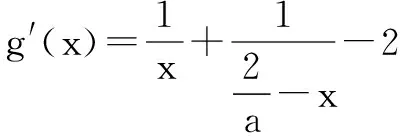求解函数极值点偏移问题的减元思想
陈芹艳
(安徽省五河县第一中学,安徽 蚌埠 233300)
求解函数极值点偏移问题的减元思想

(安徽省五河县第一中学,安徽 蚌埠 233300)
本文以在数理化解题研究2016(1)发表的极值点偏移问题的一个解题策略的文章中的四道例题为例,谈谈减元思想破解函数极值点偏移问题的可行性.
函数;极值点;偏移问题;减元思想
本文以文[1]的四道例题为例,谈谈减元思想破解函数极值点偏移问题的可行性.
例1 已知函数f(x)=xe-x,(1)求f(x)的单调区间;(2)设x1≠x2,f(x1)=f(x2),证明x1+x2>2.
解析 (1)x∈R,f′(x)=(1-x)e-x,设f′(x)=0,得x=1.f(x)在(-∞,1)上递增,在(1,+∞)上递减.
(2)不妨设x1 ∵f(x)在(-∞,1)上单调递增,所以x1+x2>2等价于f(x1)>f(2-x2),即证f(x1)=f(x2)>f(2-x2),即证f(x2)-f(2-x2)>0.构造函数g(x)=f(x)-f(2-x)=xe-x-(2-x)ex-2,x∈(1,+∞). ∵g′(x)=(1-x)(e-x-ex-2)>0,∴g(x)在(1,+∞)上单调递增,故g(x)>g(1)=0得证. 评论 本解法的思维程序为:1.根据f(x1)=f(x2)(x1≠x2)建立等量关系,并结合f(x)的单调性,确定x1,x2的取值范围. 2.不妨设x1 3.构造关于x1(或x2)的一元函数g(xi)=f(xi)-f(2a-xi)(i=1,2),应用导数研究其单调性,并借助单调性,达到待证不等式的证明. (2)不妨设x1 ∵f(x)在(-∞,0)上单调递增,欲证:x1+x2<0,即证x1<-x2问题等价于证明f(x1) 解析 (1)x∈R,f′(x)=ex-a在(-∞,+∞)上递增. (2)当a≤0时,f′(x)≥0恒成立,故f(x)在R上单调递增,不符合题意. 例4 已知函数f(x)=lnx-ax2+(2-a)x,(1)讨论f(x)的单调性;(2)若f(x)的图象与x轴交于A(x1,0),B(x2,0)两点,线段AB的中点横坐标为x0,证明f′(x0)<0. 当a≤0时,f′(x)≥0恒成立,故f(x)在(0,+∞)上单调递增,不符合题意. ∴g(x)>g′(1/a)>0,得证. 本文所述策略是解决极值点偏移问题的通性通法,实质上是把双变量的等式或不等式通过减元转化为一元变量问题求解,途径是构造一元函数,这种方法对学生来说,亲切自然,水道渠成,易于接受. [责任编辑:杨惠民] 2017-05-01 G632 B 1008-0333(2017)16-0030-02