浅谈高中数学概念研究的几点认识

戴天竹

(江苏省苏州实验中学,江苏 苏州 215000)



浅谈高中数学概念研究的几点认识

戴天竹

(江苏省苏州实验中学,江苏 苏州 215000)

本文以导数的概念、数列求和的引入为例，从多角度阐述了研究概念的重要性以及研究概念的常用方法.

定义；概念；导数；导数的定义；数列求和；放缩法

著名数学家华罗庚教授在“大哉数学之为用”一文中精采地叙述了数学的各种应用：宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁等各个方面，无处不有数学的重要贡献．他指出：数学是一切科学得力的助手和工具．它有时由于其它科学的促进而发展，有时也先走一步，领先发展，然后再获得应用．任何一门科学缺少了数学这一工具便不能确切地刻划出客观事物变化的状态，更不能从已知数据推出未知的数据来，因而就减少了科学预见的可能性，或者减弱了科学预见的精确度．数学的重要地位也带来了数学这门学科在高中教育中的重要地位．现今，高考数学对基础概念，基础技能更加重视，这也提示我们：高中数学教学中对概念深入研究是重要的．

从多角度把握概念的含义对我们解决数学问题有举足轻重的作用．本文就从多角度把握概念含义来谈谈高中数学概念的研究．

一、“数”的角度

“数形结合”是一个很重要的数学思想方法．我们就先从“数”的角度来研究，这里以导数的定义来举例．

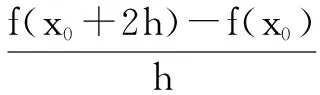
解：我们先将所求式子变形(向导数定义中式子靠拢)，有

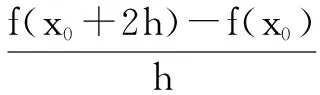
二、“形”的角度

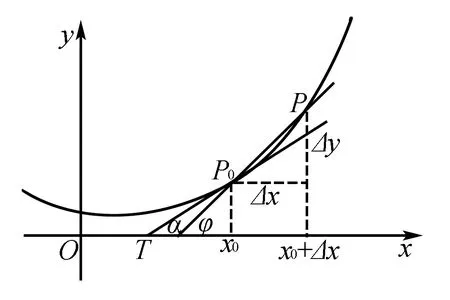
这里我们也以导数为例．导数f′(x0)的几何意义就是曲线y=f(x)在点P0(x0,f(x0))处的切线的斜率．

我们都知道切线可以用直线逼近的方法得到：设P是曲线上不同于P0的一点，随着点P沿曲线向点P0运动，割线PP0在点P0附近越来越逼近曲线在点P0处的切线．当点P无限逼近点P0时，直线PP0最终成为曲线在点P0处的切线．

如右图所示曲线，此类曲线与点P0处的切线之间还有些特殊的关系，比如将切线向上平移后与曲线有2个交点，再比如在点P0附近(除点P0外)曲线都在其切线上方．对于这类凹(凸)函数，事实上在切点附近都有类似的性质，这些相关特点在我们的解题中也有相当帮助．

解 首先，我们得到函数的定义域为[0,2]，题目中要求将函数图象绕坐标原点逆时针旋转θ，我们可以考虑将坐标轴绕坐标原点顺时针旋转θ，旋转后的图象与x轴垂直的直线至多有1个交点．原函数的图象如右图所示，坐标轴旋转后如果y轴与函数在x=x0∈(0,2)处的切线平行，则y轴与函数图象必定还有除原点外的另一个交点，即坐标轴旋转后使得y轴与函数在x=0处的切线平行是极限位置，下面求函数在x=0处的切线斜率即可．

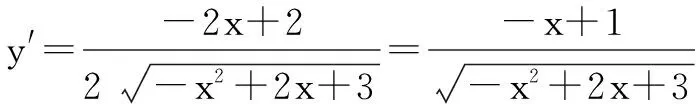
例3 已知函数f(x)的定义域为R，f(2)=3，且f(x)在R上的导函数满足f′(x)-1<0，解不等式f(x2)

三、从“引入”出发

探究概念的本质内涵，能给我们解题带来相应的思路，从定义出发，从基础概念出发往往能事半功倍，课本上定义是如此，有时课本上一些概念的引入(尤其是一些经典的引入)，更能给我们以启发．

故原不等式得证．

[1]戴荣. 对高中数学概念教学的几点认识与思考[J]. 新课程导学,2013(35):19.

[2]王韶君. 浅谈高中数学新课标理念的几点认识[J]. 中学教研(数学),2007(05):4-6.

[责任编辑：杨惠民]

2017-05-01

戴天竹(1982.11-)，男，汉，一级，硕士，从事组合数学教学.

G632

B

1008-0333(2017)16-0006-02