一道竞赛题的多种证法

张 卜

(陕西省西安市周至县第二中学,陕西 西安 710400)



一道竞赛题的多种证法

张 卜

(陕西省西安市周至县第二中学,陕西 西安 710400)

通过对1963年莫斯科数学竞赛中一道经典不等式的研究，探究出它的多种证法.

不等式;证明;竞赛题

题目 设a,b,c∈R+求证：

这是1963年莫斯科数学竞赛中的一道题，考查的是不等式最值问题，其灵活性强、难度大.笔者从不同角度来探究该题的证法.

证明1 柯西不等式法

证明2 排序不等式法

由对称性，这里不妨设a≥b≥c>0，

再由排序不等式知，顺序和≥乱序和，

证明3 换元法

令x=b+c，y=c+a，z=a+b，可求解出

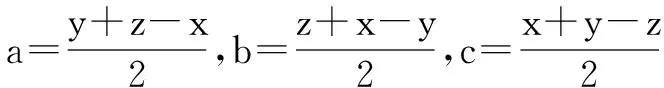
证明4 均值不等式法

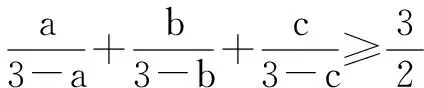
证明5 构造函数法

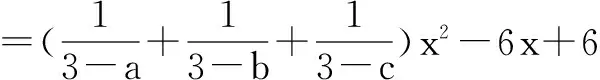
证明6 放缩法

由上式左端可以看出，三个分式的分子之和等于0，所以，在不增大各个分数值的前提下，可将它们的分母变为相等. 这里假设a≥b≥c，则有a≥1，c≤1.

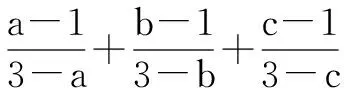
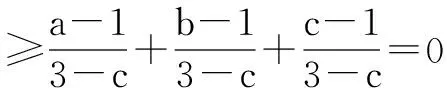
(Ⅱ)若a≥1≥b≥c，则将上述不等式左端的三个分式的分母换为3-b，即保证其中一个负分数值不变，另一个负分数值只可能减小，正分数值不增大，可得

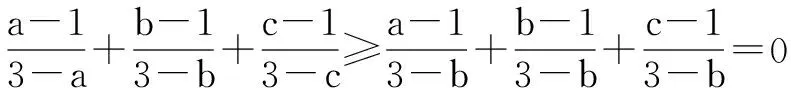
证明7 向量法

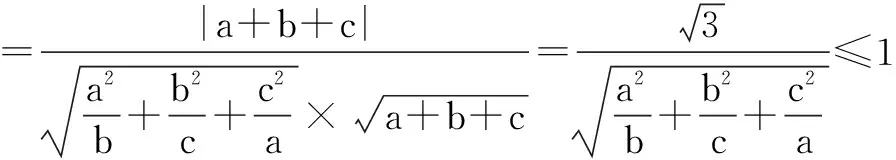
以上三式相加即证.

证明8 切线法

不等式等号成立的条件是a=b=c=1，

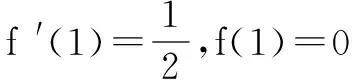
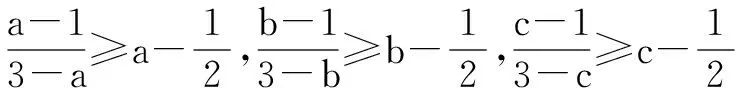
以上三式相加即证.

通过对一道竞赛题的多视角分析，开拓和启发解题思维能力和发散思维能力.根据不同的问题角度，逐一给出数学思想方法，不断地优化数学思维能力，使知识和方法融化贯通，提高自身的分析问题能力和解决问题的能力.

[1]许波.一道不等式证明题的多种解法[J].中等职业教育(理论)，2008(4).

[责任编辑：杨惠民]

2017-05-01

张卜(1987.4-),陕西省西安市高陵区,硕士,中学二级,从事高中数学教学.

G632

B

1008-0333(2017)16-0011-02