三角函数中的方程思想
王国宾
(山东省临沂第十九中学,山东 临沂 276016)
三角函数中的方程思想
王国宾
(山东省临沂第十九中学,山东 临沂 276016)
三角函数中的诸多公式均可以看作方程,因此利用方程的思想观点去分析问题、转化问题,使问题获得解决,也是我们解题的方向.本文就:(1)利用求根公式简化条件;(2)方程中的估值定角;(3)利用方程中的制约关系确定角的范围;(4)合理构建方程求值;(5)利用方程有解的充要条件求最值进行了初步探讨.
方程思想;三角函数;转化
三角函数中的诸多公式均可以看作方程,因此利用方程的思想观点去分析问题、转化问题,使问题获得解决,也是我们解题的方向.下面分析三角函数中的方程思想.
一、利用求根公式简化条件
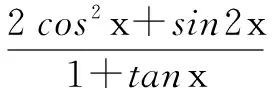
分析 题设中条件较为复杂,若考虑分解因式,则不易求解.因此可看作关于sinx(或cosx)的一个二次方程,利用二次方程求根公式可简化条件,从而达到求值的目的.
解 原方程整理为2sin2x+(cosx-6)sinx+3cosx-cos2x=0,
Δ=(cosx-6)2-8(3cosx-cos2x)=9(cosx-2)2,
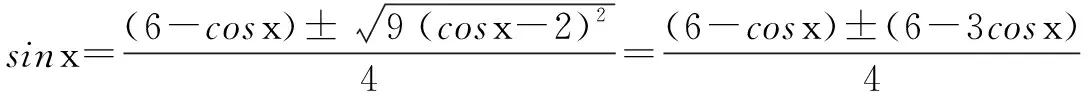




二、方程中的估值定角
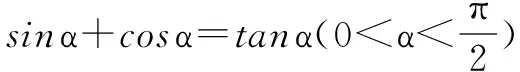

分析 角α的范围是由已知的三角方程确定,但解这个方程又超出了高中数学的范围.因此可利用α所在的范围内,有这样的α值使得方程成立的这一原理,通过估值选出正确答案,或利用数形结合的方法解决.
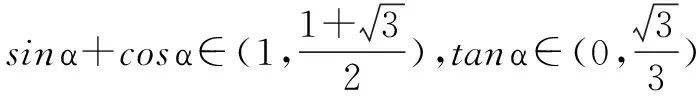


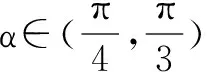
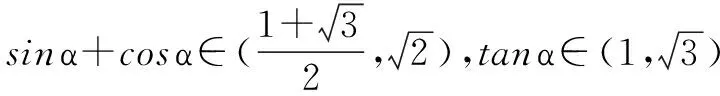

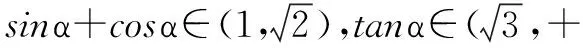
因此应选C.

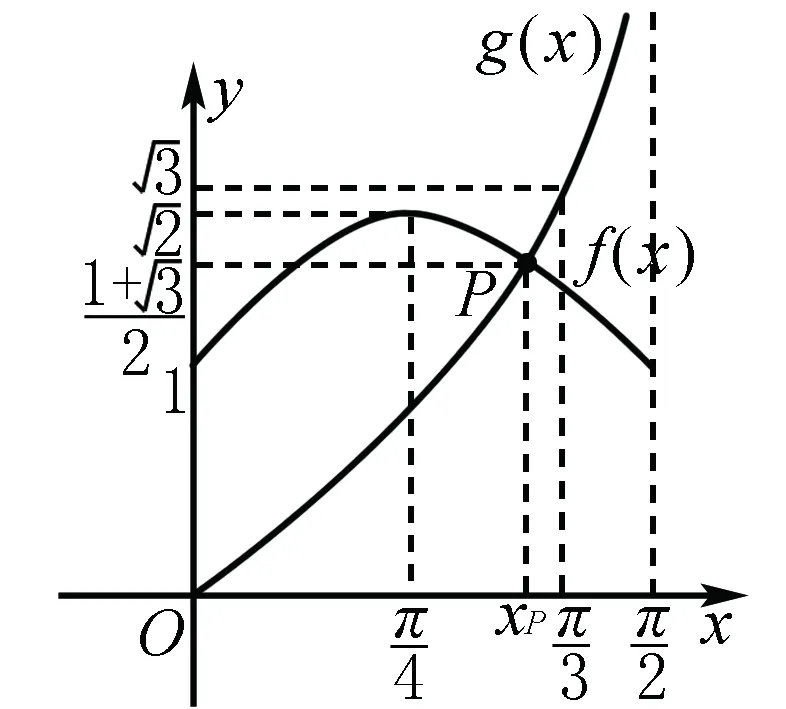
图1
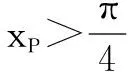
三、利用方程中的制约关系确定角的范围
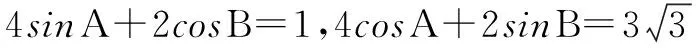
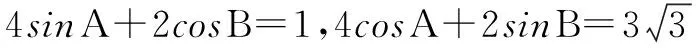
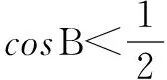
在△ABC中0° 例4 在△ABC中,BC上的中线AD=1,∠C=60°,试求△ABC面积的最大值. 图2 解 设BC=2x,AC=y,则DC=x. 在△ADC中由余弦定理得12=x2+y2-2xycos60°, 即1=x2+y2-xy≥2xy-xy=xy,所以xy≤1. 分析 将已知函数表达式去分母,整理为关于sinx的一元二次方程,根据方程有实根的条件利用判别式可求得函数的最大值. 解 已知函数整理为(1+y)sin2x+(2y-1)sinx+y=0 ①. [1]杨昌存.略谈高中数学三角函数教学策略[J].教师,2011(21). [2]王尚志、张思明、胡凤娟、付丽.整体把握高中数学新课程中的三角函数与三角[J].中学数学教学参考,2008(15). [3]南红安.利用函数与方程的思想解三角形问题[J].考试周刊,2009(50). [责任编辑:杨惠民] 2017-05-01 王国宾(1979.6-),男,山东省沂水县,本科,中学一级,从事新课程资源的开发与利用. G632 B 1008-0333(2017)16-0009-03四、合理构建方程求值

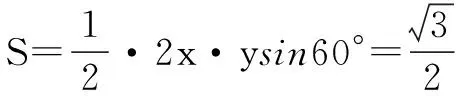

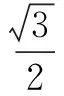
五、利用方程有解的充要条件求最值






