“空间向量的数乘运算”课堂实录*
●徐春波
(鄞江中学,浙江 宁波 315151)
“空间向量的数乘运算”课堂实录*
●徐春波
(鄞江中学,浙江 宁波 315151)
文章运用类比的方法学习空间向量的数乘运算,从概念的类比到运算的类比,再到运用向量类比证明三点共线与空间四点共面问题.整节课围绕课本中的一个四棱锥进行拆装组合,展示出任课教师设计主线清晰,课堂结构合理、流畅自然等特点.
数乘运算;共线向量;共面向量
1 课堂背景
本课例曾参加浙江省高中数学优质课比赛.赛事的主题是“高中数学课堂教学模式改进研究”,旨在展示各地优秀课改成果和教师课堂教学风采,引领新一轮课堂教学模式的改进.“空间向量的数乘运算”是笔者参赛的一节课,获省一等奖.
2 教学定位
2.1 教材分析
教科书在本小节首先类比平面向量的数乘运算引出空间向量的数乘运算以及数乘运算的分配律和结合律,进而分别给出了空间向量共线和共面的定义,并进一步研究了空间向量共线和共面的问题.本小节的教学目标是要求学生掌握空间向量数乘运算的定义和运算律,了解共线(平行)向量、共面向量的意义,掌握它们的表示方法,能理解共线向量和共面向量的定理及其推论,并能运用它们证明空间向量共线和共面的问题.
2.2 学情分析
在学生掌握了空间向量加法运算的基础上,学习空间向量的数乘运算应该没有困难,但对共面向量定理的理解和对“四点共面”问题的处理困难较大,疑惑不解,需要教师启发引导.
根据以上学情设置教学重难点如下:
重点:共面向量概念、空间向量共线定理及推论、空间向量共面定理及推论.
难点:共面向量定理及推论和四点共面的判定.2.3 教学目标
1)掌握空间向量数乘运算的定义和运算律.了解共线(平行)向量、共面向量的意义,掌握它们的表示方法.能理解共线向量和共面向量定理及其推论,并能运用它们证明与其相关的简单问题.
2)经历知识形成探索过程,逐步体会由特殊到一般和平面到空间的思维方法;体验“类比”“转化”“数形结合”等思想在空间向量中的应用.
3)通过“类比”“转化”“数形结合”等思想的应用,让学生感受和体会数学思想的魅力.
2.4 教学策略分析
整节课两条主线贯穿始终.明线以阅兵式直升机“70”编队出发提出问题,随后分析三点共线及四点共面问题,再应用到实际问题中解决问题.暗线以一个几何体“四棱锥”为背景,从基本模型中获得知识和方法.运用启发引导式教学,引导学生完成由平面到空间类比,引导学生体会降维的数学思想方法.
3 课堂实录
环节1 视频引入,提出问题.
(欣赏:抗日战争胜利70周年阅兵式剪辑.)
师:把画面切换到这张漂亮的图片当中.威武雄壮的阅兵方阵经过天安门广场,让我们感到无比自豪.更让我感兴趣的是直升飞机“70”编队队形是如何保持的.据说前后左右相邻两架飞机的间距不能超过20米,0.2秒的疏忽就可能造成相撞,飞行难度可想而知.
师:如果把飞机看成质点,我们能不能判断红线所划的3架飞机在同一直线上?能不能来判定其中的4架飞机在同一个平面内呢?假如我们在天安门某处找一个地面的观测点,用向量的方法能不能解决三点共线和四点共面呢?这就是我们今天要学习的内容.请看课题“空间向量的数乘运算”.
环节2 微课复习,类比学习.
(播放微课:平面向量数乘运算的相关知识.)
师:我们把画面定格在表1中.其中有一句话“空间中任意两个向量总是共面的”特别需要关注.我们知道空间向量的数乘研究的就是两个向量的关系,因此表1中平面向量数乘运算的知识可以类比到空间向量中来.
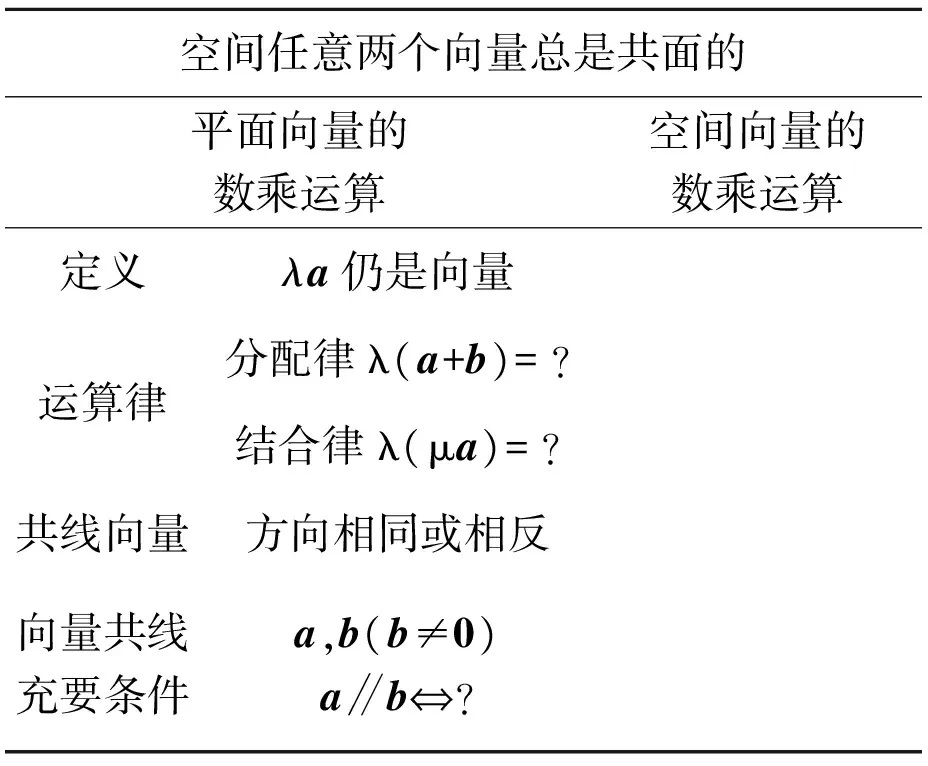
表1 向量的数乘运算
师:对于空间向量共线是这样表述的:表示空间向量的有向线段所在直线“平行”或“重合”.这和平面向量的表述本质上是一致的.在平面向量中我们已学过共线向量的充要条件,称之为共线向量定理.大家回忆一下,向量a与非零向量b共线等价于什么?请你来说一说.

图1
生:a=λb.
师:请坐,非常好!接下去,我们将围绕这些知识展开,大家把目光聚焦到黑板上这个四棱锥(如图1).
(展示PPT:在四棱锥O-EFGH中,底面EFGH为平行四边形,点A,B,C,D分别是OE,OF,OG,OH的中点.)
生:平行向量.
师:也就是共线.那么从数量上的关系来看看呢?



生:共线.
师:它们满足怎样的数量关系?

师:这些运算涉及到的实际上就是向量的数乘运算.请大家看图2(展示PPT),请问a和p共线吗?
生:不共线.
师:我们知道空间向量可以自由平移,那么能不能把a移到p所在的平面内?比如……
生:移到平面EFGH.

图2 图3
师:能不能在空间中找到一个平面和这两个向量所在直线都平行?
生:能,平移平面EFGH.
师:很好,把平面EFGH稍稍平行移动一下即可.空间内的两个向量总是可以平移到同一个平面.这样,给出共面向量的概念:我们把平行于同一个平面的向量叫做共面向量.如果给出3个空间向量呢?如图3,向量a,b,p共面吗?
生:不共面.
师:请再仔细想一想.
生:a和b共面,移上去就共面了.
师:回答得非常好.你能不能在这个图形中找一个向量(比如以A为起点)与所给出的a,b不共面?
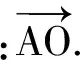
师:你还能给出其他的吗?
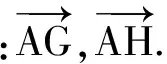
师:很好!如果3个向量无论怎么平移都不能移到同一个平面内,就说它们是不共面的3个空间向量.我们怎么来判断空间中的3个向量是共面的呢?反过来说,如果空间中的3个向量是共面的,它们又会满足怎样的等量关系呢?下面请大家通过小组合作探究来完成这个工作.
环节3 小组合作,突破难点.

图4
探究内容:如图4,对于空间任意两个不共线的向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系?反之,向量p与向量a,b有什么位置关系时,p=xa+yb?
师:第一小组请回答:如果p=xa+yb,则向量p与向量a,b有什么位置关系?
生:共面.
师:你能解释这个等量关系吗?
生:平面内一个向量能用另外两个不共线向量来表示.
师:很好!怎么看待这两个向量的和.
生:平行四边形的对角线表示的向量.
师:很棒!p就是xa,yb这两个向量构成的平行四边形的对角线.
师:追问p与xa,yb共面吗?
生:共面.
师:向量xa与a是什么关系?
生:平行向量.
师:也就是共线向量.a可以移到p,xa,yb所在的平面.向量b可以吗?
生:也可以.
师:非常好!这3个向量是什么关系呀?
生:共面.
师:第二小组请回答:反过来,向量p与向量xa,yb有什么位置关系时,p=xa+yb?
生:共面.因为p能用向量a,b来表示,所以它们在同一平面内,如果不在同一平面内,p不能用a,b表示.
师:非常好!在平面向量中,若a,b是不共线的两个向量,那么p与a,b在同一平面内,与之有关的一个非常重要的定理是什么?
生:平面向量基本定理.
(PPT展示平面向量基本定理.)
平面向量基本定理 如果两个向量a,b不共线,那么对于平面内任意向量p,有且只有一对实数x,y,使p=xa+yb.
师:刚才我们从正、反两个方面研究了3个空间向量,得到一个与之相关的空间向量共面定理.
(PPT展示空间向量共面定理.)
共面向量定理 如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p=xa+yb.
师:这两个定理有没有本质上的区别?
生:都是用不共线的两个向量来表示,没有本质区别.把这两种关系联系起来看,空间中的共面向量定理其实是平面向量基本定理的推广.
师:非常好!
环节4 分析问题,解决问题.
师:再来研究环节1提出来的三点共线和四点共面问题.
(学生跟着教师的指导,得出结论1.)



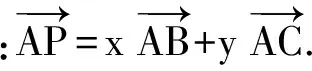
师:再类比下去还能得到什么?

师:非常好,同学们先自己尝试着做一下.
学生独自化简,教师巡视,用手机拍下学生的演算过程,并展示在投影上.教师阐述运算过程,得出结论2.


其中x′+y′+z′=1.
环节5 巩固新知,实际应用.
师:在实际问题中该怎样来解决四点共面问题呢?假如我们要把飞行的难度再加大点,如:双层飞行或者多层飞行表演,不妨来看例1.

图5
师:把图5中的各点看成飞机,也就是双层飞行表演.如果要证明其中的4个点在同一平面内,现在可以用什么方法?
生:向量共面的方法.
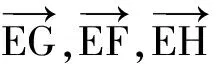

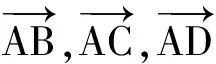
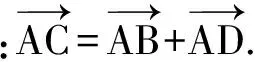
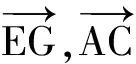
生:共线.

生:可以.

生:可以.
师:请大家接下去自己思考,把证明过程整理一下.
学生独立完成证明过程,教师巡视,适当指导,用手机拍下其中一位同学的证明过程在投影上演示,教师阐述其证明过程并在PPT上给出给出严格的证明过程.
师:这个证明过程大致可分为3步:第一步,把几何条件转化成向量表示;第二步,进行向量的运算;第三步,把向量结论转化成我们想要的几何结论.这就是我们今后在立体几何学习中,用向量法解决立体几何问题的三步曲.
环节6 课堂小结,提升认识.
师:下面,我们对这节课进行小结.我们可以从知识、方法、思想这3个角度来反思.大家一起说好吗?今天我们学习了……
生:空间向量数乘运算、向量共线与共面、三点共线以及四点共面的判断.
师:非常好!从思想方法的角度来讲呢?
生:类比、等价转化.
师:这节课我们首先是从平面向量的数乘运算类比到空间向量的数乘运算.其次,又解决了向量共线、向量共面,在此基础上研究了三点共线及四点共面问题.
开普勒曾经说过:“我珍惜类比胜于任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.”学习空间向量可类比平面向量.
�2017-03-17;
2017-04-20
徐春波(1979-),男,浙江宁波人,中学高级教师.研究方向:数学教育.
O123
A
1003-6407(2017)08-20-04

