DEPSO算法在计及UPFC设备无功优化中的应用

张 华，简献忠，肖儿良，姜冠祥，蔡留美，郑照平

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海雄博精密仪器股份有限公司，上海 200444)



DEPSO算法在计及UPFC设备无功优化中的应用

张 华1，简献忠1，肖儿良1，姜冠祥2，蔡留美2，郑照平2

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海雄博精密仪器股份有限公司，上海 200444)

针对粒子群(PSO)算法在计及UPFC无功优化中容易陷入局部最优解，提出了将差分进化粒子群(DEPSO)算法应用于计及UPFC设备的无功优化的方法。描述了添加UPFC到牛顿-拉夫逊潮流计算和将DEPSO算法应用于无功优化的方法。提出的算法在计及UPFC IEEE-30节点系统进行测试，实验表明，在计及UPFC的无功优化中，DEPSO算法较PSO算法更有效地降低了系统的有功网损，验证了文中模型和算法的有效性和可行性。

无功优化；差分进化粒子群算法；粒子群算法；统一潮流控制器

电力系统无功优化是在满足电网安全运行的前提下，通过对其控制变量的调整，使无功潮流达到最优分布，以达到降低有功网损，提高电压质量的目的。无功优化[1-2]分为传统的输电系统的无功优化和含FACTS装置的输电系统的无功优化两种，无功优化方法在文献[1]中有详细介绍。与传统的输电系统相比，引入FACTS装置后可对网络潮流分布进行更方便、快速的控制。FACTS 装置可根据需要迅速改变影响电力系统潮流分布的电压、线路阻抗和相移[2]等3个主要电气参数，UPFC设备[3-4]是FACTS 装置的杰出代表。因此开展计及UPFC的无功优化研究具有重要意义。

近期不同的人工智能算法被应用在无功优化的问题上。典型算法包括遗传算法、进化算法、细菌觅食算法、粒子群算法等。文献[4]采用粒子群算法对计及UPFC设备的无功优化进行研究，但早熟收敛是粒子群算法存在的缺陷。造成粒子群算法早熟收敛的原因是后期粒子群多样性降低，从而降低了粒子的全局搜索能力。差分进化粒子群优化算法[5]在粒子群进化过程中让部分粒子增加差分进化变异算子，这样信息的传递既来自最优粒子也来自其它粒子，以使陷入局部极小点的粒子逃出，从而增加了粒子的多样性，保证了算法的全局寻优。针对粒子群(PSO)算法在计及UPFC无功优化中容易陷入局部最优解问题，本文提出了将差分进化粒子群算法(DEPSO)应用于计及UPFC设备的无功优化中，为计及UPFC无功优化提供了一个新方法。

1 计及UPFC设备的潮流计算模型

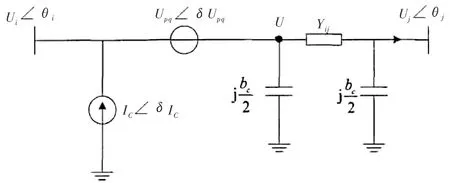
图1 UPFC等效电路图

图2 UPFC等效注入功率模型

UPFC的附加注入功率可表示为

(1)

(2)

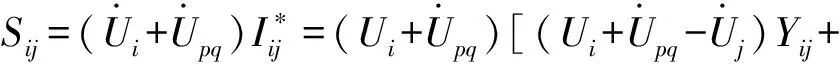
(3)

节点i，j注入的有功功率和无功功率可分别表示为

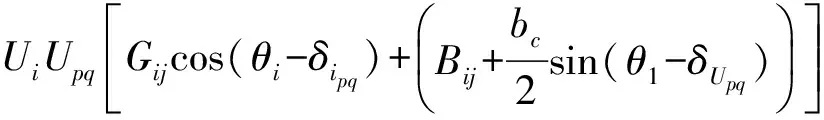
(4)

(5)

(6)

(7)

当系统装设 UPFC 后，含有 UPFC 线路的潮流方程发生变化，与原来潮流方程相比，增加了UPFC 的附加功率，用公式表示为

(8)

(9)

式中，i=1，2，…，n；j为与节点i相联的节点，集合Piinj、Qiinj分别为 UPFC 对节点i附加注入的有功功率和无功功率。

设定UPFC控制线路传输功率值为Sijref，可列出以下功率控制目标约束方程

(10)

再考虑到UPFC 装置本身的有功平衡约束，即串联电压源向系统注入的有功功率等于并联电压源从系统吸收的有功功率，其方程为

UiIccos(θi-δIc)=-UpqIijcos(δIpq-δIij)

(11)

2 计及UPFC设备的无功优化模型

在优化前，考虑到在优化过程中，状态变量发电机无功出力和节点电压可能出现越限的情况，所以本文采用经典的罚函数的形式来解决这个越限的问题[6]。

目标函数为

minf=

F(X,VL,QG)=0(潮流方程)

(13)

Xmin≤X≤Xmax

(14)

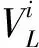
(15)

3 差分进化粒子群算法及无功优化实现

3.1 PSO算法

粒子群算法(Particle Swarm Optimization,PSO), 是Kennedy和Eberhart在1995年提出的一种进化算法。基本粒子群算法[5-8]首先初始化一群随机粒子每个粒子将在可行解空间中运动，并由速度变量决定下一位置。通常粒子将追随跟踪两个极值，一个是个体极值，另一个是全局极值，经过迭代搜索最后得到最优解。

3.2 差分进化粒子群算法

差分进化粒子群算法融合了PSO和DE算法[5,8]，它除了应用PSO更新位置和速度外，还贯穿着变异、杂交、选择运算来更新位置，这3种运算描述如下：

(1)变异。种群依据式(16)进行变异

ui,G=Xr1,G+F(Xr2,G-Xr3,G)

(16)

式中，Xr1,G,Xr2,G,Xr3,G从进化群体中随机选取的互不相同的3个个体；F为缩放比例因子；i表示不同粒子；G表示当代；G+1表示下一代；

(2)杂交。DE利用交叉算子生成新的个体 ，DE常用的交叉方式为二项式交叉，如式(17)所示

(17)

式中，j∈[1,2,…,D]，randb(j)∈[0,1]是随机数;CR是杂交参数,CR∈[0，1];IR∈[1,2,…,D]确保vij,G能从uij,G中得到至少一个参数；

(3)选择。通过比较新生成的vij,G个体与Xij,G个体的优劣，选择适应值更优的个体作为子代进入新一代。

DEPSO算法的主体过程如图3所示。

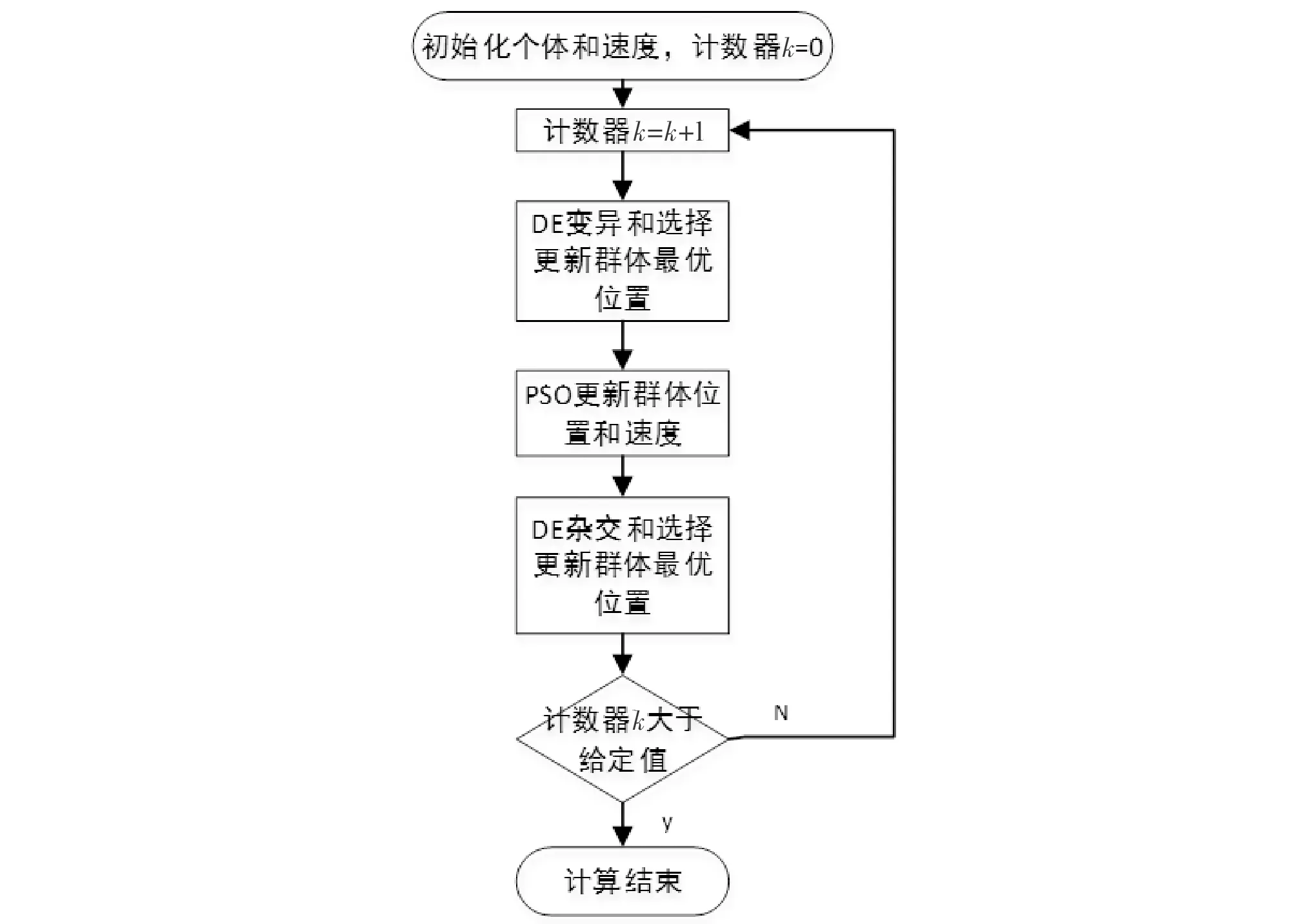
图3 DEPSO算法流程图

3.3 算法在电力系统无功优化中的实现

在电力系统中应用DEPSO算法处理无功优化问题时，粒子群在搜索空间的位置就是上文的无功优化的控制变量[VG,QC,T,VU,δU]，个体适应值[4]是位置向量代入目标函数f的结果，速度向量的取值范围是控制变量X的上下限之差,粒子的规模数将会影响到搜索的范围和寻优速度。

DEPSO在计及UPFC无功优化的处理：

(1)随机产生发电机的电压幅值，电容器的投切组数，变压器分接。形成m个可行的初始粒子群位置及速度：Xi=[VG,QC,T,VU,δU]，Vi=[V1,V2,…,VD]；

(2)根据PSO算法更新粒子的位置，计算个体适应值，更新局部最优值和全局最优值；

(3)选出群体最优位置的个体；

(4)根据式(17)对位置进行杂交、更新；

(5)根据式(16)对位置进行变异、更新；

(6)根据式(17)对位置进行杂交、更新；

(7)重复步骤(2)～步骤(6)，直到符合终止的条件。本文终止条件为最大迭代次数；

(8)输出结果。

4 算例结果及分析

本文使用Matlab进行无功优化仿真计算，以 IEEE-30节点系统为测试算例。该系统包括 6 台发电机、4 台变压器、2个并联电容器、1个UPFC 元件(安装在[9]关键路线 4-6 靠近节点4)。节点1作为平衡节点,节点2、5、8、11、13作为PV节点。平衡节点电压幅值给定为 1.05 p.u，相角值给定为0.0 rad；PV节点的有功功率值分别给定为0.4 p.u,0.0 p.u,0.0 p.u,0.0 p.u、0.0 p.u，电压幅值给定为0.95～1.10 p.u； PQ节点功率数据请见IEEE-30节点系统数据。UPFC的控制参数的取值范围，如表 1所示。

表1 UPFC控制参数的取值范围

在牛顿—拉夫逊法[7，12-13]潮流计算前，给定启动初值。PQ节点采用统一的电压初值：幅值给定为1.0 p.u，相角值给定为0.0。UPFC 元件控制变量的初始值设置如下：并联电流源幅值初始化为 0.1，相角为 0.0 rad;串联电压源幅值初始化为0.05，相角为 0.0 rad。

在基于以上启动初值下，开始牛顿—拉夫逊潮流计算，然后应用PSO算法、计及 UPFC 的PSO算法、计及 UPFC 的DEPSO算法进行优化仿真，寻找各自的最优潮流。表2为得到的各自最优潮流的数据。对比仿真结果可见，引入UPFC后，应用PSO无功优化，潮流迭代次数不变，有功网损降低； 应用DEPSO无功优化，潮流迭代次数加1次，但不影响其收敛性，有功网损降低。从有功网损最小角度看，计及 UPFC 的DEPSO算法比计及UPFC 的PSO算法对降低电网有功网损[13-15]的优化效果更好。

图4为算法迭代次数与有功网损的关系，本文迭代次数为30次。计及 UPFC 的DEPSO算法在第10次迭代前找到最小网损值，具有较好的收敛性。

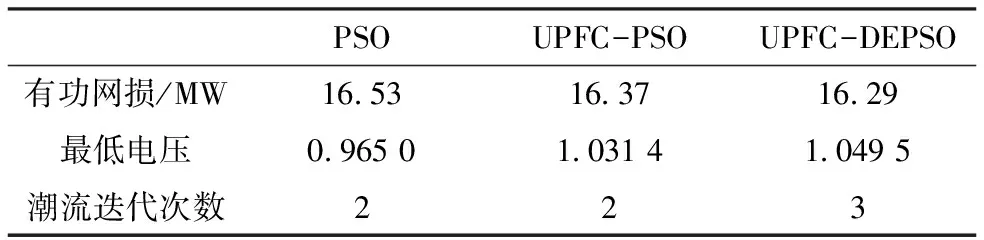
表2 无功优化后的结果

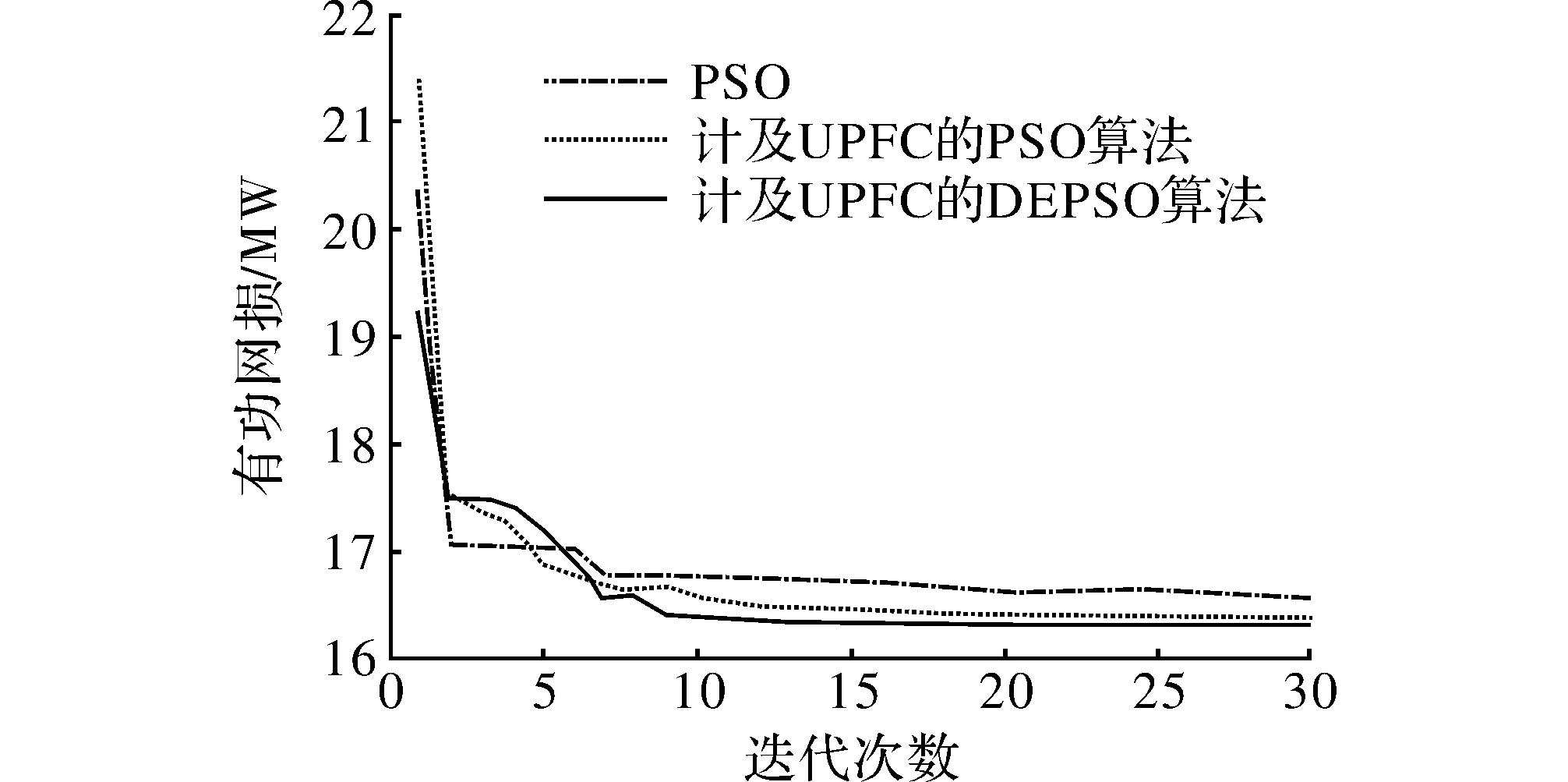
图4 算法无功优化结果

通过对 IEEE-30 节点算例的仿真分析，应用在计及UPFC的无功优化中，DEPSO算法较PSO算法能更有效降低系统的有功网损，验证了本文模型和算法的有效性和可行性，为计及UPFC无功优化提供了一种方法。

[1] 许苑.电力系统无功优化综述[J].电力系统与自动化,2010(18):153-154.

[2] 陈淮金.UPFC电力系统的潮流计算研究[J].电力系统自动化,1996,20(3):23-27.

[3] 周玲.计及UPFC的电力系统无功优化[J].中国电机工程学报,2008,28(4):37-41.

[4] 王佳.计及UPFC 电力系统无功优化研究[J].电子科技,2015,28(9):50-53.

[5] 贺安坤,苗良.差分进化微粒群优化算法—DEPSO[J].微计算机信息,2006,22(3):284-286.

[6] 付康.装设统一潮流控制器(UPFC)的电力系统电压稳定性研究[D].南宁：广西大学,2009.

[7] Fuerte Esquivel C R,Acha E. Unified power flow controller: a critical comparison of Newton-Raphson UPFC algorithms in power flow studies[J].IEE Proc-Gener Transm Distrib,1997,144(5):437-444.

[8] 郭康.基于差分进化混合粒子群算法的电力系统无功优化[J].陕西电力,2011(10):37-40.

[9] 丁晓群.结合模态分析的遗传算法在配电网无功规划中的应用[J],电网技术,2006,30(17):47-50.

[10] 蔡祯祺,黄民翔.用于风电场并网中无功电压调节的UPFC 仿真分析[J].能源工程,2010(5):29-46.

[11] 王继银.三目标自适应变异微粒群算法的无功优化[J].电子科技,2016,29(4):41-44.

[12] 邱晓燕,刘天琪.电力系统分析的计算机算法[M].北京:中国电力出版社,2009.

[13] 邱晓燕,刘天琪.电力系统分析理论[M].2版.北京:科学出版社,2011.

[14] 邱关源.电路[M].4版.北京:高等教育出版社,1999.

[15] 王兆安.谐波抑制和无功功率补偿[M].2版.北京:机械工业出版社,2015.

DEPSO ORPF Incorporating UPFC

ZHANG Hua1，JIAN Xianzhong1，XIAO Erliang1，JIANG Guanxiang2，CAI Liumei2，ZHENG Zhaoping2

(1. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2.Shanghai SUPORE Instruments Co. Ltd, Shanghai 200444, China)

The particle swarm optimization (PSO) algorithm exhibits a fast performance when optimizing reactive power flow (ORPF) incorporating UPFC. However the PSO algorithm may fall into premature convergence due to the decrease of population diversity in later evolution. A DEPSO reactive power optimization method incorporating UPFC is proposed to solve the premature convergence problem. The proposed method has the advantage of fast strong searching ability and is applied on the IEEE-30 including UPFC test system. The results demonstrate the applicability of the method.

reactive power flow optimization; DEPSO algorithm; PSO; unified power flow controller

2016- 07- 02

上海市宝山区科委产学研资助项目(bkw2015130)

张华(1988-)，男，硕士研究生。研究方向：电力系统优化分析。简献忠(1969-)，男，博士，教授。研究方向：新能源等。

10.16180/j.cnki.issn1007-7820.2017.07.018

TM761

A

1007-7820(2017)07-065-04